
20.(本小题满分13分)
对于各项均为整数的数列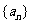 ,如果满足
,如果满足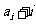 (
(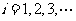 )为完全平方数,则称数列
)为完全平方数,则称数列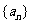 具有“
具有“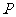 性质”;
性质”;
不论数列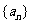 是否具有“
是否具有“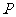 性质”,如果存在与
性质”,如果存在与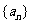 不是同一数列的
不是同一数列的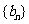 ,且
,且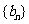 同时满足下面两个条件:①
同时满足下面两个条件:①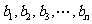 是
是 的一个排列;②数列
的一个排列;②数列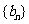 具有“
具有“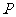 性质”,则称数列
性质”,则称数列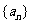 具有“变换
具有“变换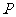 性质”.
性质”.
(Ⅰ)设数列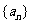 的前
的前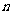 项和
项和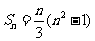 ,证明数列
,证明数列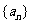 具有“
具有“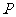 性质”;
性质”;
(Ⅱ)试判断数列 和数列
和数列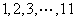 是否具有“变换
是否具有“变换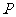 性质”,具有此性质的数列请写出相应的数列
性质”,具有此性质的数列请写出相应的数列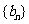 ,不具此性质的说明理由;
,不具此性质的说明理由;
(Ⅲ)对于有限项数列 ,某人已经验证当
,某人已经验证当 (
( )时,数列
)时,数列 具有“变换
具有“变换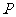 性质”,试证明:当
性质”,试证明:当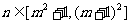 时,数列
时,数列 也具有“变换
也具有“变换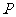 性质”.
性质”.
19.(本小题满分14分)
已知函数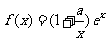 ,其中
,其中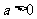 .
.
(Ⅰ)求函数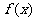 的零点;
的零点;
(Ⅱ)讨论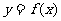 在区间
在区间 上的单调性;
上的单调性;
(Ⅲ)在区间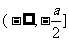 上,
上,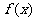 是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
18.(本小题满分14分)
椭圆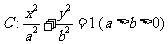 的离心率为
的离心率为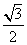 ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为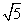 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点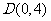 的直线
的直线 与椭圆
与椭圆 交于两点
交于两点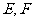 ,
, 为坐标原点,若
为坐标原点,若 为直角三角形,求直线
为直角三角形,求直线 的斜率.
的斜率.
17.(本小题满分14分)
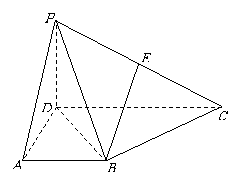
在四棱锥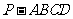 中,侧面
中,侧面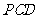
 底面
底面 ,
,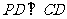 ,
,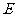 为
为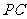 中点,底面
中点,底面 是直角梯形,
是直角梯形,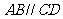 ,
,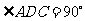 ,
,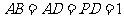 ,
,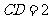 .
.
 (Ⅰ)求证:
(Ⅰ)求证: 平面
平面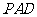 ;
;
(Ⅱ)求证: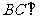 平面
平面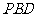 ;
;
(Ⅲ)设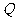 为侧棱
为侧棱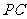 上一点,
上一点,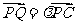 ,试确定
,试确定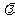 的值,使得二面角
的值,使得二面角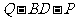 为
为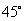 .
.
16.(本小题满分13分)
在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问题,能正确回答者进入下一轮考核,否则被淘汰. 已知某选手能正确回答第一、二、三、四轮问题的概率分别为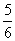 、
、 、
、 、
、 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
(Ⅲ)该选手在选拔过程中回答过的问题的个数记为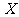 ,求随机变量
,求随机变量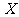 的分布列和期望.
的分布列和期望.
15.(本小题满分12分)
已知 为锐角,且
为锐角,且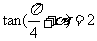 .
.
(Ⅰ)求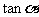 的值;
的值;
(Ⅱ)求 的值.
的值.
14. 设函数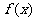 的定义域为
的定义域为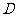 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意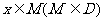 ,有
,有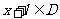 ,且
,且 ,则称
,则称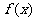 为
为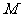 上的
上的 高调函数.
高调函数.
如果定义域是 的函数
的函数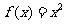 为
为 上的
上的 高调函数,那么实数
高调函数,那么实数 的取值范围是____________.
的取值范围是____________.
如果定义域为 的函数
的函数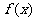 是奇函数,当
是奇函数,当 时,
时, ,且
,且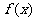 为
为 上的
上的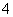 高调函数,那么实数
高调函数,那么实数 的取值范围是____________.
的取值范围是____________.
13. 已知双曲线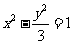 的左顶点为
的左顶点为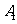 ,右焦点为
,右焦点为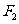 ,
,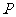 为双曲线右支上一点,则
为双曲线右支上一点,则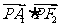 的最小值为___________.
的最小值为___________.
12. 如图,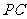 切
切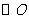 于点
于点 ,割线
,割线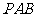 经过圆心
经过圆心 ,弦
,弦 于点
于点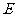 ,已知
,已知 的半径为
的半径为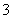 ,
,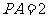 ,则
,则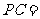 _________,
_________,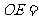 _________.
_________.
11. 极坐标方程
极坐标方程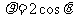 化成直角坐标方程为___________.
化成直角坐标方程为___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com