12.

由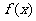在区间上为增，且图象过点，则在只有当时才满足，由偶函数的对称性可得在只有当时才满足，由函数图像的平移可得当时有.

11. 类比法：构造数列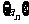，其中，则，逐步做差得：

累加求和得：

可得.

10.D 由可得：

则数列的周期为6，且，数列的前2010项从第一项起每六个作为一组，恰好可分为335组，所以.

9.Bƒ正确：二次不等式解集为，则.‚ƒ该概率为几何概型易得成立的概率为.

8.(文)D由于函数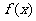为奇函数且在上为增，易知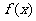在R上为增，则化为即得　　　　　 ，所以，则

(理)B.若即时，当，不等式化为不满足题意；当，不等式化为满足题意.

若，不等式恒成立即函数恒成立，则

解得，综合得.

7．A由解得为.

由可推得或者.

6．C曲线上的点到P最大、最小距离分别为6、2.

不妨将三点到点P的距离依次记为，则.

当取最大值(等于6)取最小值(等于2)时，取到最大值等于3，即q有最大值为.

当取最小值(等于2)取最大值(等于6)时，取到最小值等于，即q有最大值为.

　 因此.

5．B因为，所以tanA=d=2，，

则==12可得.

　 当时，，则为锐角三角形.

　 当时，则为钝角三角形.

4.(文)D 由可得解得.

　 因为，所以，则，

　 所以前20项和最大.

　(理)C由得，从而数列是以8为首项，为公比的等比数列.由此　　

　求出前n项和代入得，则.

3.(文)B要使得有意义，则即：

解得

(理)D 原不等式等价于或，可解得.