
13.(文)已知{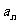 }是递增的数列,且对于任意的
}是递增的数列,且对于任意的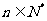 都
都
有 成立,则实数
成立,则实数 的取值范围是
的取值范围是
(理)数列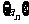 中,
中, ,且对于任意的正整数n,均有
,且对于任意的正整数n,均有 ,则实数a的取值范围是_
,则实数a的取值范围是_
12. 定义在R上的偶函数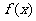 在区间
在区间 上为增函数,且函数
上为增函数,且函数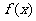 图象过点
图象过点 ,则不等式
,则不等式 的解集为
的解集为
11.在数列中, 是一个重要的公式,该公式的推导方法除了用等差数列求和公式和倒序相加法外,还可以运用如下的逐步做差,累加求和的方法:构造数列
是一个重要的公式,该公式的推导方法除了用等差数列求和公式和倒序相加法外,还可以运用如下的逐步做差,累加求和的方法:构造数列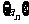 ,其中
,其中 ,则
,则 ,分别取
,分别取 逐步做差得:
逐步做差得:

累加求和得:
由此推得 。
。
类比上述方法可得
10.定义:(1)对于数列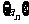 ,如果存在确定的自然数T和
,如果存在确定的自然数T和 ,使得对于一切
,使得对于一切 ,恒有
,恒有 成立,则称
成立,则称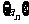 是从第
是从第 项起的周期为T的周期数列,当
项起的周期为T的周期数列,当 时,称
时,称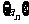 为纯周期数列;当
为纯周期数列;当 时,称
时,称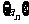 为混周期数列。(2)数列
为混周期数列。(2)数列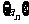 的前n项积记作
的前n项积记作 。已知纯周期数列
。已知纯周期数列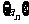 满足:
满足: ,则
,则 ( )
( )
A.  B.
B. C.
C. D.
D.
第Ⅱ卷 (非选择题,共100分)
9.给出下列四个命题:实系数二次不等式 解集为
解集为 ,则
,则 。‚
。‚ ƒ不等式
ƒ不等式 成立的概率为
成立的概率为 .其中真命题有(
)
.其中真命题有(
)
A.0 B.1 C.2 D.3
8.(文)函数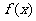 是定义在R上的奇函数,且在区间
是定义在R上的奇函数,且在区间 上为单调增函数已知不等式
上为单调增函数已知不等式 恒成立,则实数m的取值范围是( )
恒成立,则实数m的取值范围是( )
A. B.
B. C.
C. D.
D.
(理)若不等式 对任意
对任意 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A. B.
B. C.
C. D.
D.
7. 若 且
且 ,则
,则 是
是 的( )
的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件
6.曲线 上存在不同的三点到点P(4,0)的距离构成等比数列,则以下不可能成为公比q的数是( )
上存在不同的三点到点P(4,0)的距离构成等比数列,则以下不可能成为公比q的数是( )
A.  B.
B. C.
C.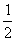 D.
D.
5.在 中,tanA是等差数列
中,tanA是等差数列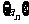 (其中
(其中 )的公差,tanB是
)的公差,tanB是 的等比中项,则
的等比中项,则 的形状是( )
的形状是( )
A. 锐角三角形 B.锐角三角形或钝角三角形
C. 钝角三角形 D.直角三角形
4.(文)等差数列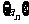 满足
满足 ,且
,且 ,前n项和为
,前n项和为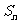 ,则
,则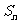 中最大的是( )
中最大的是( )
A. B.
B. C.
C. D.
D.
(理)已知数列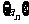 满足
满足 ,且
,且 ,前n项和为
,前n项和为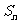 ,则满足不等式
,则满足不等式 的最小正整数n是(
)
的最小正整数n是(
)
A.5 B.6 C.7 D.8
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com