
1. 若函数 与
与 的定义域为分别为
的定义域为分别为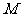 、
、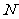 ,则
,则 等于
等于
A. B.
B. C.
C.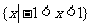 D.
D.
21.解:(1)由 可得
可得 , (1分,文科2分)
, (1分,文科2分)
所以数列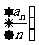 是以2为首项,
是以2为首项,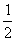 为公比的等比数列,
为公比的等比数列,
则 从而
从而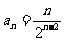 . (3分,文科5分)
. (3分,文科5分)
(2)由(1)知 是2为首项,
是2为首项,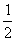 为公比的等比数列,
为公比的等比数列,
所以 ,
,
不等式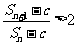 化为
化为 ,(4分,文科8分)
,(4分,文科8分)
即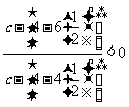 -------
-------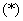 ,由于
,由于
所以 化简为
化简为 (6分,文科11分)
(6分,文科11分)
又 ,
,
所以 ,即存在这样的实数c满足要求.(8分,文科14分)
,即存在这样的实数c满足要求.(8分,文科14分)
(3)(理科做)由(1)得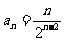 ,
,
代入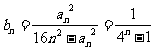 , (9分)
, (9分)
所以:
当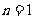 时,
时, (10分)
(10分)
当 时,
时,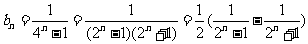
 (12分)
(12分)
又 且
且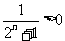
所以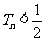 . (14分)
. (14分)
20.解:(1) 由 知
知 ,故当
,故当 时
时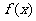 取得最小值为
取得最小值为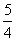 ,
,
即 (4分)
(4分)
⑵ 由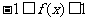 得
得 即
即 对于任意
对于任意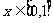 恒成立,
恒成立,
当 时,
时, ,则
,则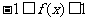 恒成立;
恒成立;
|
 时,有
时,有
对于任意的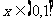 恒成立;
恒成立; ,则
,则 ,故要使①式恒成立,则有
,故要使①式恒成立,则有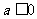 ,又
,又
 ;又
;又 ,则有
,则有 ,综上所述:
,综上所述: .(8分)
.(8分)
⑶ 当 时,
时, ,则此二次函数的对称轴为
,则此二次函数的对称轴为 ,开口向上,
,开口向上,
故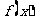 在
在 上为单调递增函数,且当
上为单调递增函数,且当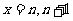 时,
时, 均为整数,
均为整数,
故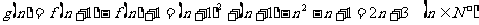 ,
,
则数列 的通项公式为
的通项公式为 ,故
,故 ①
①
又 ②
②
由①-②得 .
.
 ,∴
,∴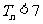 .(13分)
.(13分)
19.解:(1)因为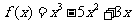 ,则
,则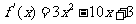 (1分)
(1分)
令 解得
解得 ,又
,又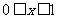 得
得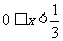 ,
,
同理:令 解得
解得 ,(4分)
,(4分)
从而函数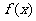 在区间
在区间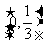 上递增,在区间
上递增,在区间 上递减.(5分)
上递减.(5分)
(2)因为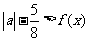 即
即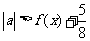 ,
,
令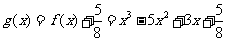 (7分)
(7分)
由(1)得函数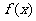 在区间
在区间 上递减,
上递减,
则函数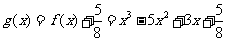 在区间
在区间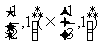 上
上
为减函数. (9分)
所以在 上,当
上,当 时有
时有 ,即总有
,即总有 成立,而
成立,而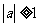 .
.
所以a的取值范围是 . (12分)
. (12分)
18.解:数列求和问题,先是递增数列然后是递减数列。 设第x天达到最大量,则第X天运送食品量为1000+100(x-1)(暂且用B表示该式)(4分)
最后一天运送量为B-100(15-X)=200X-600(暂且用C表示该式) (8分)
则等式为(1000+B)X/2+(B+C)(15-X)/2=21300 (10分)
然后把B,C代入即可解的X=9 (12分)
17.(文)当x>0,y=lnx为上凸函数,(6分)
就有
 (理)证明:取
(理)证明:取 (
(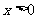 )
)
 ,
,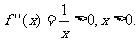 (6分)
(6分)
 . 由琴生不等式有
. 由琴生不等式有
即有 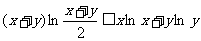 (12分)
(12分)
16. (文)解:当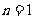 时,
时, (1分)
(1分)
当 时,
时,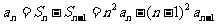 整理得:
整理得: (2分)
(2分)
则: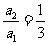 ,
,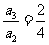 ,
, ,
, ,
,
累乘得:
所以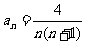 ,检验得
,检验得 也满足该式
也满足该式
所以数列的通项公式是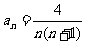 .(6分)
.(6分)
因为
所以:
 (12分)
(12分)
(理)解:(1)∵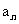 =4
=4 -4
-4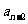
∴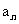 -2
-2 =2
=2 -4
-4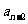 (1分)
(1分)
∴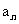 -2
-2 =2(
=2( -2
-2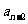 )即
)即 =2
=2
则{ }成以
}成以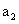 -2
-2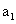 为首项,以2为公比的等比数列
为首项,以2为公比的等比数列
∴ =(
=(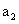 -2
-2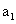 )*
)*
得 =
= ∴
∴ +
+
∴ =
= +1 (4分)
+1 (4分)
∴数列{ }成以
}成以 为首项,以1为公差的等差数列
为首项,以1为公差的等差数列
∴ =
= +(n-1)*1 即
+(n-1)*1 即 =n+1
=n+1
∴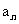 =(n+1)
=(n+1) (7分)
(7分)
(2)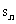 =2*
=2* +3*
+3*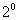 +4*
+4* +…+(n+1)
+…+(n+1)
2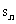 =2*
=2*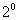 +3*
+3* +4*
+4* +……+n
+……+n +(n+1)
+(n+1)
上两式相减得:
-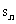 =2*
=2* +
+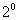 +
+ +…+
+…+ -(n+1)
-(n+1)
∴-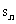 =2*
=2* +
+ -(n+1)
-(n+1)
∴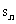 =n*
=n* (12分)
(12分)
15. 4
点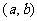 在区域
在区域 内,则
内,则 。
。
令P ,则
,则 代入上式可得
代入上式可得
在直角坐标系内作出点P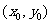 表示的区域,可求得面积为4.
表示的区域,可求得面积为4.
14.(文)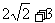
由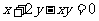 得
得 ,从而
,从而
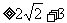 所以
所以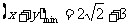 .
.
(理)4
因为:
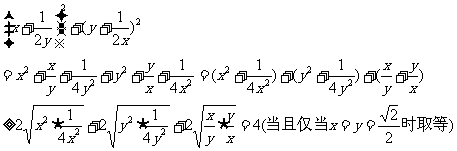
所以其最小值为4.
13.(文)
因为{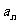 }是递增数列,则对
}是递增数列,则对 有
有 恒成立,即
恒成立,即 整理得:
整理得: ,所以
,所以 .
.
(理)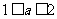 将式子平方再化简,舍去等差的情况,又递推求出通项公式,再利用恒成立即可
将式子平方再化简,舍去等差的情况,又递推求出通项公式,再利用恒成立即可
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com