
22、在平面直角坐标系中,已知矩形ABCD中,边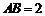 ,边
,边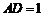 ,且AB、AD分别在x轴、y轴的正半轴上,点A与坐标原点重合.将矩形折叠,使点A落在边DC上,设点
,且AB、AD分别在x轴、y轴的正半轴上,点A与坐标原点重合.将矩形折叠,使点A落在边DC上,设点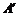 是点A落在边DC上的对应点.
是点A落在边DC上的对应点.
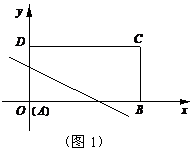 (1)当矩形ABCD沿直线
(1)当矩形ABCD沿直线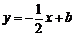 折叠时(如图1),
折叠时(如图1),
求点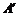 的坐标和b的值;
的坐标和b的值;
(2)当矩形ABCD沿直线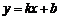 折叠时,
折叠时,
①求点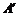 的坐标(用k表示);求出k和b之间的关系式;
的坐标(用k表示);求出k和b之间的关系式;
②如果我们把折痕所在的直线与矩形的位置分
为如图2、3、4所示的三种情形,
请你分别写出每种情形时k的取值范围.(将答案直接填在每种情形下的横线上)
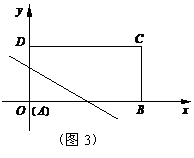
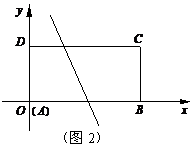
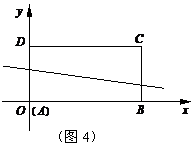
k的取值范围是 ; k的取值范围是 ;k的取值范围是 ;
21、如图10,已知抛物线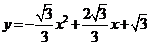 与
与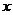 轴的两个交点为
轴的两个交点为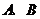 ,与y轴交于点
,与y轴交于点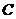 .
.
(1)求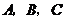 三点的坐标;
三点的坐标;
(2)求证: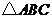 是直角三角形;
是直角三角形;
(3)若坐标平面内的点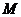 ,使得以点
,使得以点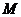 和三点
和三点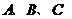 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点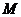 的坐标.(直接写出点的坐标,不必写求解过程)
的坐标.(直接写出点的坐标,不必写求解过程)
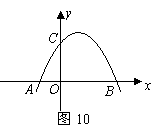
20、如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
(1)试找出一个与△AED全等的三角形,并加以证明.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.
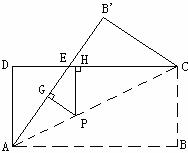
19、某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
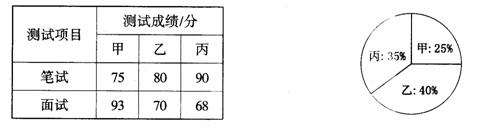
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如上图所示,每得一票记作1分.
(l)请算出三人的民主评议得分;
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到0.01)?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定个人成绩,那么谁将被录用?
18、某风景区对5个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变。有关数据如下表所示:
|
景点 |
A |
B |
C |
D |
E |
|
原价(元) |
10 |
10 |
15 |
20 |
25 |
|
现价(元) |
5 |
5 |
15 |
25 |
30 |
|
平均日人数(千人) |
1 |
1 |
2 |
3 |
2 |
(1)该风景区称调整前后这5个景点门票的平均收费不变,平均日总收入持平。问风景区是怎样计算的?
(2)另一方面,游客认为调整收费后风景区的平均日总收入相对于调价前,实际上增加了约9.4%。问游客是怎样计算的?
(3)你认为风景区和游客哪一个的说法较能反映整体实际?
17、如图所示:一次函数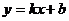 的图象与反比例函数
的图象与反比例函数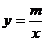 的图象交于A、B两点,
的图象交于A、B两点,
⑴ 利用图中的条件,求一次函数与反比例函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的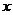 的取值范围;
的取值范围;
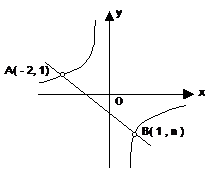
16、如图,已知△ABC,∠ACB=90º,AC=BC,点E、
F在AB上,∠ECF=45º,
(1)求证:△ACF∽△BEC(5分)
(2)设△ABC的面积为S,求证:AF·BE=2S(3)

15、某同学在A、B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元。
(1)求该同学看中的随身听和书包单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
14、作图证明
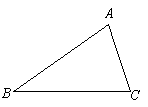 如图,在
如图,在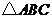 中,作
中,作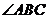 的平分线
的平分线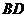 ,交
,交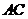 于
于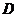 ,作线段
,作线段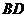 的垂直平分线
的垂直平分线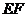 ,分别交
,分别交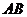 于
于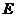 ,
,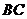 于
于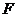 ,垂足为
,垂足为 ,连结
,连结 .在所作图中,寻找一对全等三角形,并加以证明.(不写作法,保留作图痕迹)
.在所作图中,寻找一对全等三角形,并加以证明.(不写作法,保留作图痕迹)
13、解不等式组,并把其解集在数轴上表示出来:
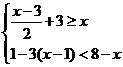
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com