
5.已知双曲线 的离心率为
的离心率为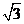 ,右准线方程为
,右准线方程为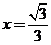 .
.
(Ⅰ)求双曲线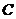 的方程;
的方程;
(Ⅱ)设直线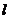 是圆
是圆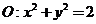 上动点
上动点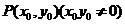 处的切线,
处的切线,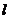 与双曲线
与双曲线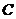 交于不同的两点
交于不同的两点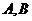 ,证明
,证明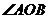 的大小为定值.
的大小为定值.
4.09,北京,理8.点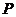 在直线
在直线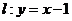 上,若存在过
上,若存在过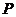 的直线交抛物线
的直线交抛物线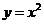 于
于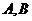 两点,且
两点,且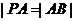 ,则称点
,则称点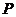 为“
为“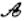 点”,那么下列结论中正确的是 ( )
点”,那么下列结论中正确的是 ( )
A.直线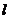 上的所有点都是“
上的所有点都是“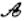 点”
B.直线
点”
B.直线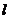 上仅有有限个点是“
上仅有有限个点是“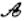 点”
点”
C.直线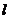 上的所有点都不是“
上的所有点都不是“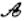 点” D.直线
点” D.直线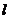 上有无穷多个点(点不是所有的点)是“
上有无穷多个点(点不是所有的点)是“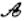 点”
点”
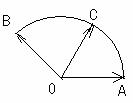
3.(2009,安徽,理14) 给定两个长度为1的平面向量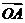 和
和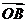 ,它们的夹角为
,它们的夹角为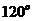 。如图所示,点C在以O为圆心的圆弧
。如图所示,点C在以O为圆心的圆弧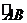 上变动。若
上变动。若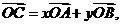 其中
其中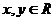 ,则
,则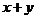 的最大值是________。
的最大值是________。
2.在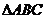 中,
中,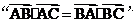 是
是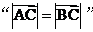 的
的
A充分非必要条件 B必要非充分条件
 C充分必要条件
D非充分非必要条件
C充分必要条件
D非充分非必要条件
1.过椭圆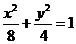 的焦点作两条互相垂直的直线分别交椭圆于
的焦点作两条互相垂直的直线分别交椭圆于 和
和 ,求四边形
,求四边形 的面积的最小值和最大值.
的面积的最小值和最大值.
1.(2007年高考安徽文科第18题)
设F是抛物线G:x2=4y的焦点.
(Ⅰ)过点P(0,-4)作抛物线G的切线,求切线方程;
(Ⅱ)设A、B为势物线G上异于原点的两点,且满足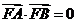 ,延长AF、BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值.
,延长AF、BF分别交抛物线G于点C,D,求四边形ABCD面积的最小值.
案例22 (2008年高考全国Ⅱ理科第21题、文22题)
设椭圆中心在坐标原点,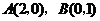 是它的两个顶点,直线
是它的两个顶点,直线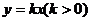 与
与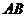 相交于点
相交于点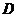 ,与椭圆相交于
,与椭圆相交于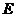 、
、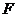 两点.
两点.
(Ⅰ)若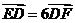 ,求
,求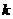 的值;
的值;
(Ⅱ)求四边形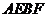 面积的最大值.
面积的最大值.
(以上可参见《高考大问题--动感设计轻松破解数学压轴题》第一章 )
命题3.过原点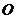 作双曲线
作双曲线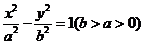 的两条相互垂直的弦AC,BD,且
的两条相互垂直的弦AC,BD,且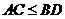 则四边形ABCD的面积的最大值不存在,最小值为取值范围为
则四边形ABCD的面积的最大值不存在,最小值为取值范围为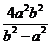 .
.
研究视角由面积转向弦长
命题4.若AC,BD为圆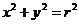 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为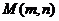 ,则
,则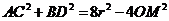 .
.
命题5.过原点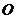 作椭圆
作椭圆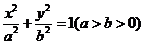 的两条相互垂直的弦AC,BD,则
的两条相互垂直的弦AC,BD,则
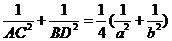 .
.
命题6.过原点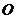 作椭圆
作椭圆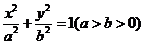 的两条相互垂直的弦AC,BD,则
的两条相互垂直的弦AC,BD,则
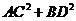 的最小值
的最小值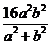 .
.
命题7.过原点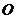 作双曲线
作双曲线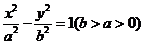 的两条相互垂直的弦AC,BD,则
的两条相互垂直的弦AC,BD,则
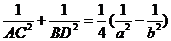 .
.
高考试题链接:
案例25 (2008年高考安徽文科第22题)
设椭圆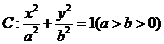 其相应于焦点
其相应于焦点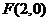 的准线方程为
的准线方程为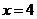 .
.
(Ⅰ)求椭圆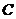 的方程;
的方程;
(Ⅱ)已知过点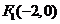 倾斜角为
倾斜角为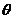 的直线交椭圆
的直线交椭圆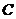 于
于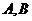 两点,求证:
两点,求证:
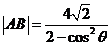 ;
;
(Ⅲ)过点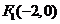 作两条互相垂直的直线分别交椭圆
作两条互相垂直的直线分别交椭圆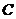 于
于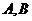 和
和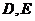 ,求
,求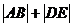 的最小值.
的最小值.
1.引例:(09,全国2,理16)
已知AC,BD为圆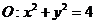 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为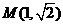 ,则四边形ABCD的面积的最大值为
.
,则四边形ABCD的面积的最大值为
.
命题1.若AC,BD为圆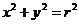 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为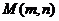 ,则四边形ABCD面积的取值范围为:
,则四边形ABCD面积的取值范围为: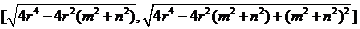 .
.
 命题2.过原点
命题2.过原点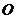 作椭圆
作椭圆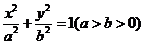 的两条相互垂直的弦AC,BD,则四边形ABCD的面积的取值范围为
的两条相互垂直的弦AC,BD,则四边形ABCD的面积的取值范围为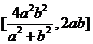 .当且仅当弦AC,BD分别是椭圆的长、短轴时,四边形ABCD的面积最大;当且仅当
.当且仅当弦AC,BD分别是椭圆的长、短轴时,四边形ABCD的面积最大;当且仅当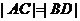 时,四边形ABCD的面积最小.
时,四边形ABCD的面积最小.
高考试题链接:
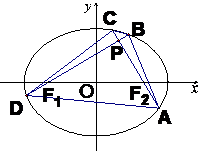
案例27 .(2007年高考全国Ⅰ理科第21题、文科第22题)
已知椭圆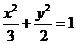 的左右焦点分别为
的左右焦点分别为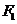 、
、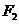 ,过
,过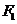 的直线交椭圆于B、D两点,过
的直线交椭圆于B、D两点,过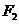 的直线交椭圆于A、C两点,且
的直线交椭圆于A、C两点,且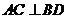 ,垂足为P
,垂足为P
(Ⅰ)设P点的坐标为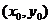 ,证明:
,证明: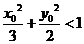 ;
;
(Ⅱ)求四边形ABCD的面积的最小值.
变式练习
5.在变化中求发展
4.重在过程--强调知识的来龙去脉
3.强化基础、加强主干,重点整合、构建网络
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com