
2.导数的几何意义
1.曲线的切线及切线的斜率;
2.求曲线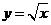 在点
在点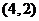 处的切线.
处的切线.
1.求曲线y=f(x)=x3在点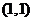 处的切线;
处的切线;
例1:(1)求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.
(2)求函数y=3x2在点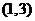 处的导数.
处的导数.
解:(1)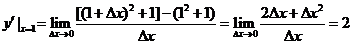 ,
,
所以,所求切线的斜率为2,因此,所求的切线方程为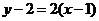 即
即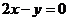
(2)因为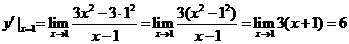
所以,所求切线的斜率为6,因此,所求的切线方程为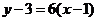 即
即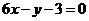
(2)求函数f(x)=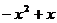 在
在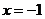 附近的平均变化率,并求出在该点处的导数.
附近的平均变化率,并求出在该点处的导数.
解: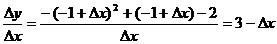
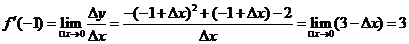
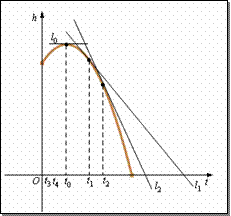 例2.(课本例2)如图3.1-3,它表示跳水运动中高度随时间变化的函数
例2.(课本例2)如图3.1-3,它表示跳水运动中高度随时间变化的函数
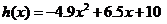 ,根据图像,请描述、比较曲线
,根据图像,请描述、比较曲线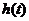 在
在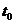 、
、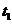 、
、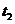 附近的变化情况.
附近的变化情况.
解:我们用曲线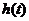 在
在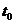 、
、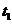 、
、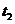 处的切线,刻画曲线
处的切线,刻画曲线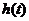 在上述三个时刻附近的变化情况.
在上述三个时刻附近的变化情况.
(1) 当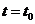 时,曲线
时,曲线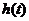 在
在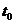 处的切线
处的切线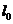 平行于
平行于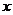 轴,所以,在
轴,所以,在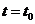 附近曲线比较平坦,几乎没有升降.
附近曲线比较平坦,几乎没有升降.
(2) 当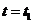 时,曲线
时,曲线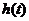 在
在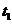 处的切线
处的切线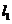 的斜率
的斜率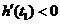 ,所以,在
,所以,在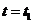 附近曲线下降,即函数
附近曲线下降,即函数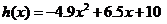 在
在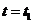 附近单调递减.
附近单调递减.
(3) 当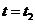 时,曲线
时,曲线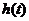 在
在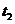 处的切线
处的切线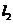 的斜率
的斜率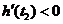 ,所以,在
,所以,在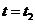 附近曲线下降,即函数
附近曲线下降,即函数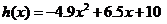 在
在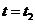 附近单调递减.
附近单调递减.
从图3.1-3可以看出,直线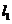 的倾斜程度小于直线
的倾斜程度小于直线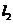 的倾斜程度,这说明曲线在
的倾斜程度,这说明曲线在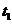 附近比在
附近比在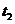 附近下降的缓慢.
附近下降的缓慢.
例3.(课本例3)如图3.1-4,它表示人体血管中药物浓度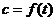 (单位:
(单位: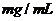 )随时间
)随时间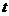 (单位:
(单位: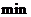 )变化的图象.根据图像,估计
)变化的图象.根据图像,估计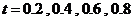 时,血管中药物浓度的瞬时变化率(精确到
时,血管中药物浓度的瞬时变化率(精确到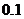 ).
).
 解:血管中某一时刻药物浓度的瞬时变化率,就是药物浓度
解:血管中某一时刻药物浓度的瞬时变化率,就是药物浓度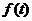 在此时刻的导数,从图像上看,它表示曲线
在此时刻的导数,从图像上看,它表示曲线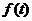 在此点处的切线的斜率.
在此点处的切线的斜率.
如图3.1-4,画出曲线上某点处的切线,利用网格估计这条切线的斜率,可以得到此时刻药物浓度瞬时变化率的近似值.
作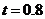 处的切线,并在切线上去两点,如
处的切线,并在切线上去两点,如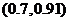 ,
,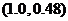 ,则它的斜率为:
,则它的斜率为: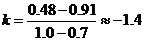
所以 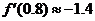
下表给出了药物浓度瞬时变化率的估计值:
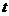 |
0.2 |
0.4 |
0.6 |
0.8 |
药物浓度瞬时变化率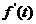 |
0.4 |
0 |
-0.7 |
-1.4 |
(三)函数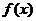 在点
在点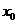 处的导数
处的导数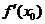 、导函数
、导函数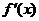 、导数 之间的区别与联系。
、导数 之间的区别与联系。
(1)函数在一点处的导数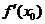 ,就是在该点的函数的改变量与自变量的改变量之比的极限,它是一个常数,不是变数。
,就是在该点的函数的改变量与自变量的改变量之比的极限,它是一个常数,不是变数。
(2)函数的导数,是指某一区间内任意点x而言的, 就是函数f(x)的导函数
(3)函数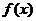 在点
在点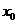 处的导数
处的导数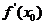 就是导函数
就是导函数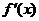 在
在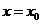 处的函数值,这也是 求函数在点
处的函数值,这也是 求函数在点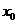 处的导数的方法之一。
处的导数的方法之一。
(二)导函数:
由函数f(x)在x=x0处求导数的过程可以看到,当时,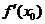 是一个确定的数,那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.记作:
是一个确定的数,那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.记作: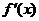 或
或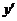 ,
,
即: 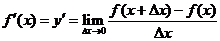
注:在不致发生混淆时,导函数也简称导数.
(二)导数的几何意义:
函数y=f(x)在x=x0处的导数等于在该点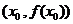 处的切线的斜率,
处的切线的斜率,
即 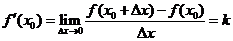
说明:求曲线在某点处的切线方程的基本步骤:
①求出P点的坐标;
②求出函数在点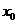 处的变化率
处的变化率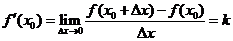 ,得到曲线在点
,得到曲线在点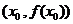 的切线的斜率;
的切线的斜率;
③利用点斜式求切线方程.
(一)曲线的切线及切线的斜率:如图3.1-2,当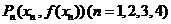 沿着曲线
沿着曲线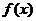 趋近于点
趋近于点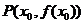 时,割线
时,割线 的变化趋势是什么?
的变化趋势是什么?
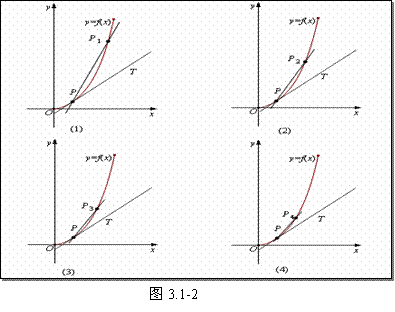
我们发现,当点 沿着曲线无限接近点P即Δx→0时,割线
沿着曲线无限接近点P即Δx→0时,割线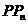 趋近于确定的位置,这个确定位置的直线PT称为曲线在点P处的切线.
趋近于确定的位置,这个确定位置的直线PT称为曲线在点P处的切线.
问题:⑴割线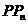 的斜率
的斜率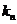 与切线PT的斜率
与切线PT的斜率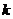 有什么关系?
有什么关系?
⑵切线PT的斜率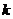 为多少?
为多少?
容易知道,割线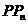 的斜率是
的斜率是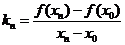 ,当点
,当点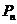 沿着曲线无限接近点P时,
沿着曲线无限接近点P时,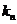 无限趋近于切线PT的斜率
无限趋近于切线PT的斜率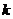 ,即
,即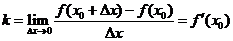
说明:(1)设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.
这个概念: ①提供了求曲线上某点切线的斜率的一种方法;
②切线斜率的本质-函数在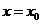 处的导数.
处的导数.
(2)曲线在某点处的切线:1)与该点的位置有关;2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.
(二)瞬时速度、导数
我们知道,导数表示函数y=f(x)在x=x0处的瞬时变化率,反映了函数y=f(x)在x=x0附近的变化情况,导数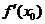 的几何意义是什么呢?
的几何意义是什么呢?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com