
5.正、余弦定理是解三角形的最主要工具;涉及三角形中的两个(或三个)角的问题常用正弦定理,只涉及三角形中的一个角常用余弦定理。关注两定理在解相关实际问题中的运用。
[举例1]已知⊿ABC中,角A、B、C所对的边分别为a,b,c,且BC边上的高为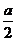 ,则
,则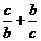 的最大值为:
的最大值为:
A.2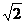 B.
B. 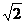 C. 2
D.4
C. 2
D.4
 解析:
解析: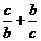 =
=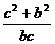 ,这个形式很容易联想到余弦定理:cosA=
,这个形式很容易联想到余弦定理:cosA=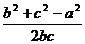 ①
①
而条件中的“高”容易联想到面积,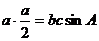
即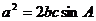 ②,将②代入①得:
②,将②代入①得:
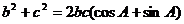
∴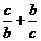 =2(cosA+sinA)=2
=2(cosA+sinA)=2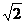 sin(A+
sin(A+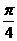 ),当A=
),当A=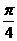 时取得最大值2
时取得最大值2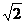 ,故选A。
,故选A。
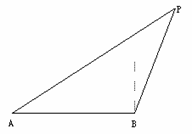
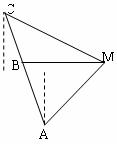 [举例2] 如图,已知A、B、C是一条直路上的三点,
[举例2] 如图,已知A、B、C是一条直路上的三点,
AB与BC各等于1千米,从三点分别遥望塔M,在
A处看见塔在北偏东450方向,在B处看见塔在正
东方向,在C处看见塔在南偏东600方向,求塔到
直路ABC的最短距离。
解析:已知AB=BC=1,∠AMB=450,∠CMB=300,∴∠CMA=750
易见⊿MBC与⊿MBA面积相等,∴AM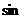 450= CM
450= CM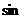 300
300
即CM=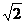 AM,记AM=
AM,记AM=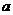 ,则CM=
,则CM=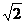
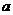 ,在⊿MAC中,AC=2,由余弦定理得:
,在⊿MAC中,AC=2,由余弦定理得:
4=3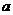 2-2
2-2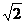
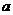 2cos750,∴
2cos750,∴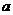 2=
2=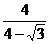 ,记M到AC的距离为
,记M到AC的距离为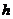 ,则
,则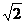
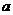 2sin750=2
2sin750=2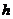
得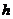 =
=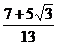 ,∴塔到直路ABC的最短距离为
,∴塔到直路ABC的最短距离为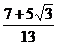 。
。
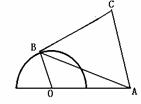 [巩固1] 如图,半圆O的直径为2,A为直径延长线上一点,且OA=2,B为半圆周长上任意一点,以AB为边作等边△ABC,问B点在什么位置时,四边形OACB的面积最大,并求出这个最大面积.
[巩固1] 如图,半圆O的直径为2,A为直径延长线上一点,且OA=2,B为半圆周长上任意一点,以AB为边作等边△ABC,问B点在什么位置时,四边形OACB的面积最大,并求出这个最大面积.
[巩固2] 一艘海岸缉私艇巡逻至A处时发现在其正东方向20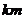 的海面B处有一艘走私船正以
的海面B处有一艘走私船正以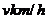 的速度向北偏东300的方向逃窜,缉私艇以
的速度向北偏东300的方向逃窜,缉私艇以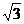
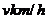 的速度沿
的方向追击,才能最快截获走私船?若
的速度沿
的方向追击,才能最快截获走私船?若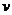 =40
=40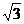 ,则追击时间至少为 分钟。
,则追击时间至少为 分钟。
简答
4.关注正弦定理中的“外接圆”直径,涉及三角形外接圆直径的问题多用正弦定理。
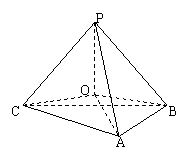 [举例] △ABC中,AB=9,AC=15,∠BAC=1200,它所在平面外一点P到△ABC三个顶点的距离是14,那么点P到平面ABC的距离是: 。
[举例] △ABC中,AB=9,AC=15,∠BAC=1200,它所在平面外一点P到△ABC三个顶点的距离是14,那么点P到平面ABC的距离是: 。
解析:记P在平面ABC上的射影为O,∵PA=PB=PC
∴OA=OB=OC,即O是△ABC的外心,只需求出OA(△ABC
的外接圆的半径),记为R,在△ABC中由余弦定理知:
BC=21,在由正弦定理知:2R=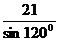 =14
=14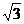 ,∴OA=7
,∴OA=7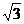
得:PO=7。
[巩固]已知⊙O的半径为R,若它的内接△ABC中,2R(sin2A-sin2C)=(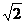 a-b)sinB,求(1)∠C的大小;(2)△ABC的面积的最大值。
a-b)sinB,求(1)∠C的大小;(2)△ABC的面积的最大值。
[迁移]直线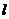 :
: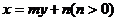 过点
过点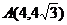 ,若可行域
,若可行域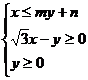 的外接圆直径为
的外接圆直径为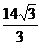 ,则实数
,则实数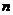 的值是______________
的值是______________
3.三角形内的三角函数问题中,既涉及到边又涉及到角时,往往需要进行边角转换,正、余弦定理是实现三角形边角转换的仅有的工具。对a、b、c(或sinA、sinB、sinC)的齐次式,可以直接用正弦定理转换;而对a、b、c平方的和差形式,常用余弦定理转换。
[举例1] ⊿ABC的三内角的正弦值的比为4:5:6,则三角形的最大角为 。
解析:由正弦定理得:⊿ABC三边的比为4:5:6,不妨设a=4k,b=5k,c=6k,(k>0)
则边c所对的角C为最大角,cosC=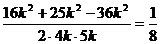 ,∴C=arccos
,∴C=arccos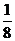 。
。
[举例2]在⊿ABC中,角A、B、C所对的边分别为a、b、c,若a2+b2=6c2,则
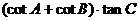 的值为
的值为
解析:对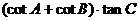 “切化弦”得:
“切化弦”得: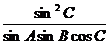 ,再由正弦定理得
,再由正弦定理得
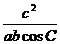 ,再对cosC使用余弦定理得:
,再对cosC使用余弦定理得: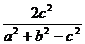 ,将a2+b2=6c2,代入接得原式等于
,将a2+b2=6c2,代入接得原式等于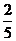 。
。
[巩固1] 若△ABC三边成等差数列,则B的范围是 ;若△ABC三边成等比数列,则B的范围是 ;
[巩固2]若三角形三边a、b、c满足a2+c2=b2+ac,且a:c=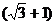 :2,求角C的大小。
:2,求角C的大小。
[迁移]已知⊿ABC中,sinA(sinB+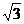 cocB)=
cocB)=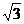 sinC,BC=3,则⊿ABC的周长的取值范围是
sinC,BC=3,则⊿ABC的周长的取值范围是
。
2.关注点、函数图象(曲线)按某向量平移导致的坐标、解析式(方程)的变化;点M(x,y)按向量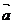 (m,n)平移得到点M‘(x+m,y+n);曲线C:f(x,y)=0按向量
(m,n)平移得到点M‘(x+m,y+n);曲线C:f(x,y)=0按向量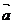 (m,n)平移得到曲线
(m,n)平移得到曲线
C/:f(x-m,y-n)=0。函数图象(曲线)按某向量平移的问题可以先“翻译”成向左(右)、向上(下)平移,再按函数图象变换的规律“图进标退”操作。[注意]:向量无论怎样平移,其坐标都不发生变化。
[举例] 将直线x-by+1=0按向量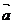 =(1,-1)平移后与圆x2-4x+y2+3=0相切,则k= 。
=(1,-1)平移后与圆x2-4x+y2+3=0相切,则k= 。
解析:思路一:直线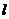 :x-by+1=0按向量
:x-by+1=0按向量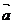 平移即“向右、向下各平移1个单位”,亦即:x变为x-1,y变为y+1,得直线
平移即“向右、向下各平移1个单位”,亦即:x变为x-1,y变为y+1,得直线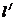 :x-by-b=0,圆:(x-2)2+ y2=1,
直线
:x-by-b=0,圆:(x-2)2+ y2=1,
直线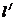 与圆相切,则有:
与圆相切,则有:
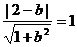 得b=
得b=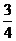 。思路二:圆M:(x-2)2+ y2=1按向量-
。思路二:圆M:(x-2)2+ y2=1按向量-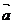 平移(x变成x+1,y变成y-1)后得:圆M/:(x-1)2+(y-1)2=1, 圆M/与直线
平移(x变成x+1,y变成y-1)后得:圆M/:(x-1)2+(y-1)2=1, 圆M/与直线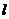 :x-by+1=0相切,有
:x-by+1=0相切,有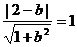 得b=
得b=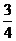 。
。
思路三:圆心M(2,0)按向量-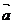 平移后得M/(1,1),M/到直线
平移后得M/(1,1),M/到直线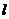 的距离为1。
的距离为1。
[巩固1]已知点A(1,2)、B(4,2),向量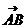 按
按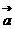 =(1,3)平移后所得向量的坐标为( )
=(1,3)平移后所得向量的坐标为( )
(A)(3,0) (B)(4,3) (C)(-4,-3) (D)(-4,3)
[巩固2]若把一个函数的图象按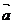 =(-
=(-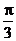 ,-2)平移后得到函数y=cosx的图象,则原图象的函数解析式为
: A.y=cos(x+
,-2)平移后得到函数y=cosx的图象,则原图象的函数解析式为
: A.y=cos(x+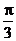 )-2;
B.y=cos(x-
)-2;
B.y=cos(x-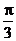 )-2;
)-2;
C.y=cos(x+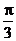 )+2;
D.y=cos(x-
)+2;
D.y=cos(x-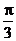 )+2
)+2
[迁移]已知函数f(x)= -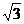 sinxcosx+3cos2x-
sinxcosx+3cos2x-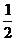 ,x∈R
,x∈R
(1)
将f(x)表示成Asin(2x+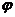 )+B的形式(其中A>0,0<
)+B的形式(其中A>0,0<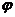 <2
<2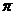 )
)
(2)
将y=f(x)的图象按向量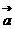 平移后,所得到的图象关于原点对称,求使|
平移后,所得到的图象关于原点对称,求使|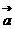 | 得最小的向量
| 得最小的向量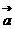 。
。
1.若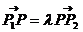 ,则称点
,则称点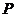 分有向线段
分有向线段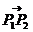 所成的比为λ。注意:“定比”不是“比”,点分有向线段所成的比,是用数乘向量定义的,而不是两个向量的比。当
所成的比为λ。注意:“定比”不是“比”,点分有向线段所成的比,是用数乘向量定义的,而不是两个向量的比。当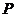 为外分点时λ为负,内分点时λ为正,
为外分点时λ为负,内分点时λ为正,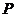 为中点时λ=1,若起点
为中点时λ=1,若起点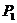 (x1,y1),终点
(x1,y1),终点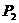 (x2,y2),则分点
(x2,y2),则分点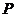 (x0,y0)的坐标为:x0=
(x0,y0)的坐标为:x0=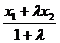 ,y0=
,y0=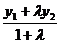 。由此推出:中点公式及三角形的重心公式:在⊿ABC中,若A(x1,y1)、B(x2,y2)、C(x3,y3),则⊿ABC的重心G(
。由此推出:中点公式及三角形的重心公式:在⊿ABC中,若A(x1,y1)、B(x2,y2)、C(x3,y3),则⊿ABC的重心G(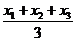 ,
,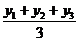 )。
)。
[举例1]设O(0,0),A(1,0),B(0,1),点P是线段AB上的一个动点,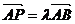 ,若
,若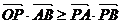 ,则λ的去值范围是:
,则λ的去值范围是:
A.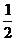 ≤λ≤1 B.1-
≤λ≤1 B.1-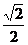 ≤λ≤1 C.
≤λ≤1 C.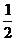 ≤λ≤1+
≤λ≤1+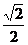 D.1-
D.1-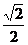 ≤λ≤1+
≤λ≤1+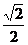
解析:思路一: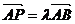
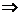
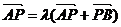
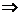
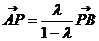 ,即P分有向线段
,即P分有向线段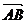 所成的比为
所成的比为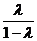 ,由定比分点坐标公式得:P(1-λ,λ),于是有
,由定比分点坐标公式得:P(1-λ,λ),于是有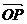 =(1-λ,λ),
=(1-λ,λ),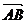 =(-1,1),
=(-1,1),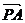 =(λ,-λ),
=(λ,-λ),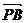 =(λ-1,1-λ),∴λ-1+λ≥λ(λ-1)- λ(1-λ)
=(λ-1,1-λ),∴λ-1+λ≥λ(λ-1)- λ(1-λ)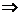
2λ2-4λ+1≤0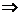 1-
1-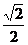 ≤λ≤1+
≤λ≤1+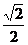 。思路二:记P(x,y),由
。思路二:记P(x,y),由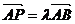 得:
得:
(x-1,y)=(-λ, λ)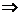 x=1-λ,y=λ即P(1-λ,λ),以下同“思路一”。
x=1-λ,y=λ即P(1-λ,λ),以下同“思路一”。
思路三: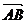 =(-1,1),
=(-1,1),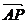 =(-λ,λ),
=(-λ,λ),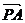 =(λ,-λ),
=(λ,-λ),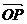 =
=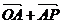 =(1-λ,λ),
=(1-λ,λ),
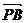 =
=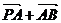 =(λ-1,1-λ),以下同“思路一”。
=(λ-1,1-λ),以下同“思路一”。
[举例2]已知⊿ABC中,点B(-3,-1),C(2,1)是定点,顶点A在圆(x+2)2+(y-4)2=4上运动,求⊿ABC的重心G的轨迹方程。
解析:记G(x,y),A(x0,y0),由重心公式得:x=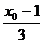 ,y=
,y=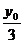 ,于是有:x0=3x+1,y0=3y,
,于是有:x0=3x+1,y0=3y,
而A点在圆(x+2)2+(y-4)2=4上运动,∴(3x+1+2)2+(3y-4)2=4,化简得:
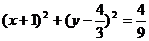 。
。
[巩固]已知P是曲线C:y=xn(n∈N﹡)上异于原点的任意一点,过P的切线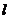 分别交X轴,Y轴于Q、R两点,且
分别交X轴,Y轴于Q、R两点,且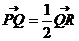 ,求n的值。
,求n的值。
[迁移]已知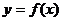 是定义在R上的单调函数,实数
是定义在R上的单调函数,实数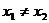 ,
,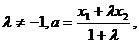
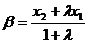 ,若
,若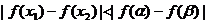 ,则 ( )
,则 ( )
A.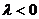 B.
B.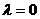 C.
C.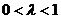 D.
D.
18.下列两篇作文题,任选其中的一篇,按要求写作。
(1)以“灵魂高于行走的双脚”为题,写一篇的文章。(70分)
要求:明确立意,文体自选(诗歌除外);不得抄袭;字数不少于800字。
(2)近年来,临近岁末腊月,汉字文化圈就流行对“年度汉字”的评选,即:借汉字的言简意赅、具有高度概括性的特点,评选出一个最能代表该年度的大众心情、象征该年度世态变化、反映该年度社会焦点的汉字。在2009年岁末,《羊城晚报》《重庆晨报》《厦门商报》等报纸以及网络媒体纷纷举行“年度汉字”的评选,“被”“牛”“生”“拆”等汉字分别被评为2000年“年度汉字”。
请你从“被”“牛”“生”“拆”四个2009年“年度汉字”中选择一个汉字,写一篇作文。
要求:①理解你选择的这个汉字作为“年度汉字”的内涵;②题目自拟;③文体自定;④字数不少于800字。
16.根据提供的两个例句,写出新词语“半糖”的意思。(3分)
例1:半糖哲学之一:一半成熟一半幼稚,做人才有意思。
半糖哲学之二:一半聪明一半愚笨,大智若愚最好。
例2:写程序的时候也要注意劳逸结合,入迷了也不好,不入迷也不好,要有所入迷,还能迅速退出,尝到甜头就走,所以叫半糖程序。
“半糖”的意思是:_ 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com