
2.已知函数f(x)=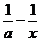 (a>0,x>0).
(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是增函数;
(2)若f(x)≤2x在(0,+∞)上恒成立,求a的取值范围;
(3)若f(x)在[m,n]上的值域是[m,n](m≠n),求a的取值范围.
1.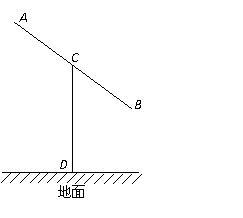 某建筑的金属支架如图所示,根据要求
某建筑的金属支架如图所示,根据要求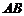 至少长2.8m,
至少长2.8m,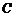 为
为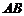 的中点,
的中点,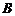 到
到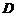 的距离比
的距离比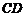 的长小0.5m,
的长小0.5m,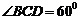 ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计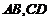 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?
3.(1) 函数和方程是密切相关的,对于函数y=f(x),当y=0时,就转化为方程f(x)=0,也可以把函数式y=f(x)看做二元方程y-f(x)=0。函数问题(例如求函数的值域等)可以转化为方程问题来求解,方程问题也可以转化为函数问题来求解,如解方程f(x)=0,就是求函数y=f(x)的零点。
(2) 函数与不等式也可以相互转化,对于函数y=f(x),当y>0时,就转化为不等式f(x)>0,借助于函数图像与性质解决有关问题,而研究函数的性质,也离不开解不等式。
(3) 数列的通项或前n项和是自变量为正整数的函数,用函数的观点处理数列问题十分重要。
(4) 解析几何中的许多问题,例如直线和二次曲线的位置关系问题,需要通过解二元方程组才能解决,涉及到二次方程与二次函数的有关理论。
(5) 立体几何中有关线段、角、面积、体积的计算,经常需要运用布列方程或建立函数表达式的方法加以解决。
[思想方法]
[例1](2009年高考山东卷理科第20题)
等比数列{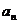 }的前n项和为
}的前n项和为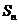 ,已知对任意的
,已知对任意的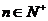 ,点
,点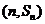 ,均在函数
,均在函数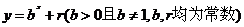 的图像上.
的图像上.
(Ⅰ)求r的值;
(Ⅱ)当b=2时,记 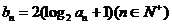
证明:对任意的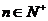 ,不等式
,不等式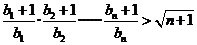 成立
成立
[解析](Ⅰ) 由题意知: 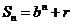 ,
,
当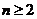 时,
时,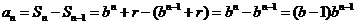 ,
,
由于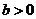 且
且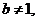 所以当
所以当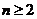 时, {
时, {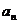 }是以
}是以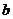 为公比的等比数列,
为公比的等比数列,
又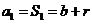 ,
,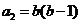 ,
,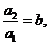 即
即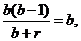 解得
解得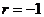 .
.
(Ⅱ)∵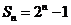 ,∴当
,∴当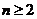 时,
时,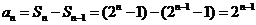 ,
,
又当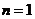 时,
时, 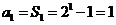 ,适合上式,∴
,适合上式,∴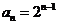 ,
,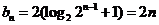 ,
,
∴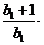
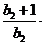
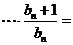
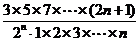 ,
,
下面用数学归纳法来证明不等式: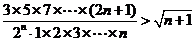
证明:(1)当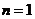 时,左边=
时,左边=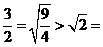 右边,不等式成立.
右边,不等式成立.
(2)假设当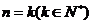 时,不等式成立,即
时,不等式成立,即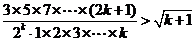 ,
,
则当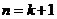 时,
时,
不等式左边=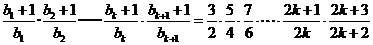
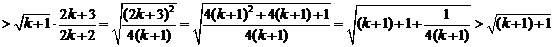
所以当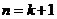 时,不等式也成立,
时,不等式也成立,
综上(1)(2)可知:当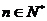 时,不等式
时,不等式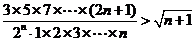 恒成立,
恒成立,
所以对任意的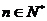 ,不等式
,不等式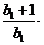
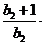
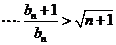 成立.
成立.
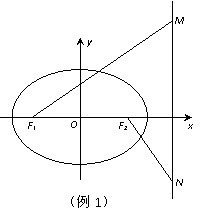 [例2]如图,椭圆
[例2]如图,椭圆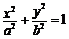 (a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,且
(a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,且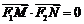 .
.
(1)设C是以MN为直径的圆,试判断原点O与圆C的位置关系;
(2)设椭圆的离心率为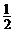 ,MN的最小值为
,MN的最小值为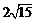 ,求椭圆方程.
,求椭圆方程.
[解](1)设椭圆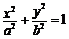 的焦距为2c(c>0),
的焦距为2c(c>0),
则其右准线方程为x=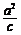 ,且F1(-c, 0), F2(c, 0). 、
,且F1(-c, 0), F2(c, 0). 、
设M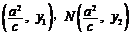 ,
,
则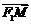 =
=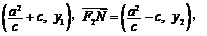
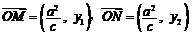 .
.
因为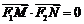 ,所以
,所以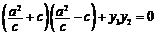 ,即
,即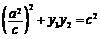 .
.
于是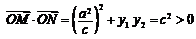 ,故∠MON为锐角.
,故∠MON为锐角.
所以原点O在圆C外.
(2)因为椭圆的离心率为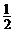 ,所以a=2c,
,所以a=2c,
于是M 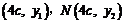 ,且
,且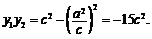
MN2=(y1-y2)2=y12+y22-2y1y2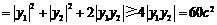 .
.
当且仅当
y1=-y2=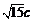 或y2=-y1=
或y2=-y1=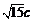 时取“=”号,
时取“=”号,
所以(MN)min= 2c=2,于是c=1, 从而a=2,b=,
故所求的椭圆方程是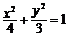 .
.
[例3]已知函数f(x)=x2–(m+1)x+m(m∈R)
(1)若tanA,tanB是方程f(x)+4=0的两个实根,A、B是锐角三角形ABC的两个内角.求证:m≥5;
(2)对任意实数α,恒有f(2+cosα)≤0,证明m≥3;
(3)在(2)的条件下,若函数f(sinα)的最大值是8,求m.
解析:(1)证明:f(x)+4=0即x2–(m+1)x+m+4=0.依题意:
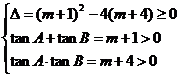 又A、B锐角为三角形内两内角
又A、B锐角为三角形内两内角
∴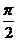 <A+B<π
<A+B<π
∴tan(A+B)<0,即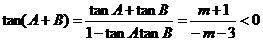
∴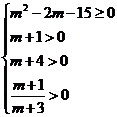 ∴m≥5
∴m≥5
(2)证明:∵f(x)=(x–1)(x–m)
又–1≤cosα≤1,∴1≤2+cosα≤3,恒有f(2+cosα)≤0
即1≤x≤3时,恒有f(x)≤0即(x–1)(x–m)≤0
∴m≥x但xmax=3,∴m≥xmax=3
(3)解:∵f(sinα)=sin2α–(m+1)sinα+m=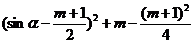
且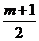 ≥2,∴当sinα=–1时,f(sinα)有最大值8.
≥2,∴当sinα=–1时,f(sinα)有最大值8.
即1+(m+1)+m=8,∴m=3
[例4]某厂家拟在2009年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)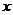 万件与年促销费用
万件与年促销费用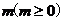 万元满足
万元满足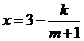 (
(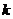 为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2009年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2009年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2009年该产品的利润y万元表示为年促销费用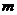 万元的函数;
万元的函数;
(2)该厂家2009年的促销费用投入多少万元时,厂家的利润最大?
解:(1)由题意可知,当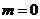 时,
时,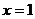 ,∴
,∴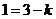 即
即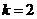 ,
,
∴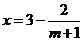 ,每件产品的销售价格为
,每件产品的销售价格为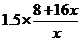 元.
元.
∴2009年的利润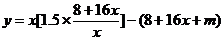
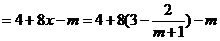
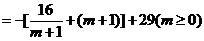
(2)∵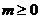 时,
时,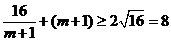 .
.
∴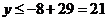 ,当且仅当
,当且仅当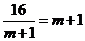 ,即
,即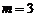 时,
时,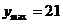 .
.
答:该厂家2009年的促销费用投入3万元时,厂家的利润最大,最大为21万元.
[专题演练]
2.方程的思想,就是分析数学问题中变量间的等量关系,建立方程或方程组,或者构造方程,通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决。方程的数学是对方程概念的本质认识,用于指导解题就是善于利用方程或方程组的观点观察处理问题。方程思想是动中求静,研究运动中的等量关系.
1.函数的思想,是用运动和变化的观点,分析和研究数学中的数量关系,建立函数关系或构造函数,运用函数的图像和性质去分析问题、转化问题,从而使问题获得解决。函数思想是对函数概念的本质认识,用于指导解题就是善于利用函数知识或函数观点观察、分析和解决问题。
21.(本小题满分14分)已知数列 的相邻两项
的相邻两项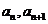 是关于
是关于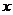 的方程
的方程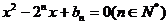 的两实根,且
的两实根,且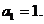
(1)求证:数列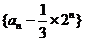 是等比数列;
是等比数列;
(2)设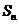 是数列
是数列 的前
的前 项和,求
项和,求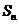 ;
;
(3)问是否存在常数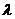 ,使得
,使得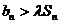 对
对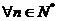 都成立,若存在,求出
都成立,若存在,求出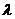 的取值范围,若不存在,请说明理由。
的取值范围,若不存在,请说明理由。
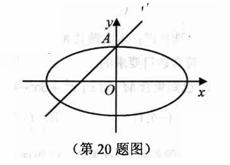
20.(本小题满分14分)如图所示,椭圆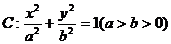 的离心率为
的离心率为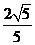 ,且A(0,1)是椭圆C的顶点。
,且A(0,1)是椭圆C的顶点。
(1)求椭圆C的方程;
(2)过点A作斜率为1的直线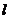 ,在直线
,在直线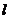 上求一点M,使得以椭圆C的焦点为焦点,且过点M的双曲线E的实轴最长,并求此双曲线E的方程。
上求一点M,使得以椭圆C的焦点为焦点,且过点M的双曲线E的实轴最长,并求此双曲线E的方程。
19.(本题满分14分)已知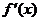 是
是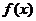 的导函数,
的导函数,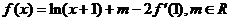 ,且函数
,且函数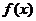 的图象过点(0,-2)。
的图象过点(0,-2)。
(1)求函数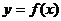 的表达式;
的表达式;
(2)设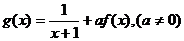 ,若
,若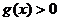 在定义域内恒成立,求实数
在定义域内恒成立,求实数 的取值范围。
的取值范围。
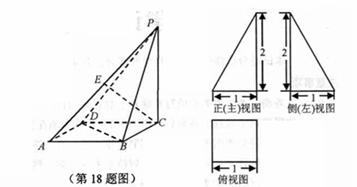
18.(本小题满分14分)已知四棱锥P-ABCD的三视图如下右图所示,其中正(主)视图与侧(左)视为直角三角形,俯视图为正方形。
(1)求四棱锥P-ABCD的体积;
 (2)若E是侧棱
(2)若E是侧棱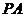 上的动点。问:不论点E在PA的任何位置上,是否都有
上的动点。问:不论点E在PA的任何位置上,是否都有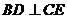 ?请证明你的结论?
?请证明你的结论?
(3)求二面角D-PA-B的余弦值。
17.(本小题满分12分)第16届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下2×2列联表:
|
|
喜爱运动 |
不喜爱运动 |
总计 |
|
男 |
10 |
|
16 |
|
女 |
6 |
|
14 |
|
总计 |
|
|
30 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)从女志原者中抽取2人参加接待工作,若其中喜爱运动的人数为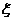 ,求
,求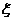 的分布列和均值。
的分布列和均值。
参考公式: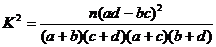 ,其中
,其中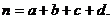
参考数据:
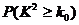 |
0.40 |
0.25 |
0.10 |
0.010 |
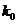 |
0.708 |
1.323 |
2.706 |
6.635 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com