误解：因为共有人民币10张，每张人民币都有取和不取2种情况，减去全不取的1种情况，共有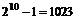种.

错因分析：这里100元面值比较特殊有两张，在误解中被计算成 4 种情况，实际上只有不取、取一张和取二张3种情况.

正解：由分析，共有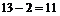个解集不同的一元二次方程.

6未考虑特殊情况出错

在排列组合中要特别注意一些特殊情况，一有疏漏就会出错.

例9 现有1角、2角、5角、1元、2元、5元、10元、50元人民币各一张，100元人民币2张，从中至少取一张，共可组成不同的币值种数是（    ）

(A)1024种   (B)1023种   (C)1536种   (D)1535种

错因分析：误解中没有注意到题设中：“求解集不同的……”所以在上述解法中要去掉同解情况，由于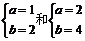同解、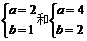同解，故要减去2个。

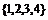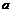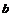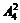误解：从集合中任意取两个元素作为、，方程有个，当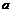、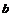取同一个数时方程有1个，共有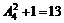个.

例8 已知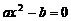是关于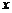的一元二次方程，其中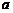、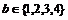，求解集不同的一元二次方程的个数.

正解：当使用四种颜色时，由前面的误解知有48种着色方法；当仅使用三种颜色时：从4种颜色中选取3种有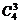种方法，先着色第一区域，有3种方法，剩下2种颜色涂四个区域，只能是一种颜色涂第2、4区域，另一种颜色涂第3、5区域，有2种着色方法，由乘法原理有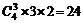种.综上共有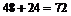：种.

误解：先着色第一区域，有4种方法，剩下3种颜色涂四个区域，即有一种颜色涂相对的两块区域，有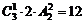种，由乘法原理共有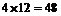：种.

错因分析：据报导，在高考中有很多考生填了48种.这主要是没有看清题设“有4种颜色可供选择”，不一定需要4种颜色全部使用，用3种也可以完成任务.

在解决排列组合问题时一定要注意题目中的每一句话甚至每一个字和符号，不然就可能多解或者漏解.

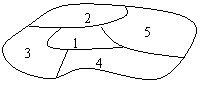
例7  (2003全国高考题)如图，一个

地区分为5个行政区域，现给地图着色，

要求相邻区域不得使用同一颜色，现有4

种颜色可供选择，则不同的着色方法共有          种.（以数字作答）

正解：任一个五位的奇数都符合要求，共有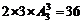个，再由前面分析四位数个数和五位数个数之和共有72个，选D.

5忽视题设条件出错

法，剩下3个数排中间两个位置有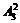种排法，共有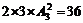个.

错因分析：误解只考虑了四位数的情况，而比1000大的奇数还可能是五位数.