
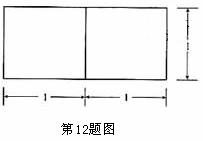
12.若一个底面是正三角形的三棱柱的正 视图如图所示,则其表面积等于
.
视图如图所示,则其表面积等于
.
[答案]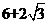
[解析]由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以底面积为
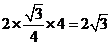 ,侧面积为
,侧面积为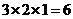 ,所以其表面积为
,所以其表面积为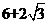 。K^S*5U.C#O%
。K^S*5U.C#O%
[命题意图]本题考查立体几何中的三视图,考查同学们识图的能力、空间想象能力等基本能力。
13.[答案]4
[解析]设球半径为r,则由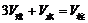 可得
可得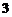
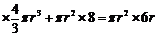 ,解得r=4.
,解得r=4.
(2010福建理数)
13.(2010湖北理数)圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm。
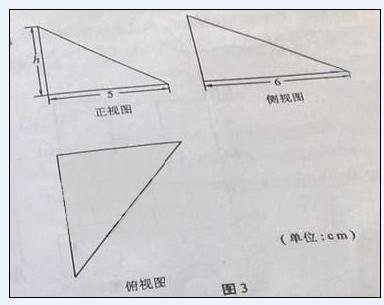
13.(2010湖南理数)图3中的三个直角三角形是 一个体积为20
一个体积为20 的几何体的三视图,则
的几何体的三视图,则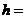
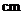 .
.


14.(2010湖北文数)圆柱形容器内盛有高度为3cm的水,若放入三个相同的珠(球的半么与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是____cm.
[答案]4
[解析]设球半 径为r,则由
径为r,则由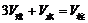 可得
可得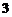
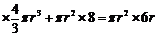 ,解得r=4.
,解得r=4.
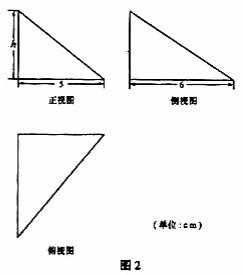
13.(2010湖南文数)图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= 4 cm
(2010浙江理数)(12)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是___________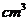 .
.
 解析:图为一四棱台和长方体的组合体的三视图,由卷中所给公式计算得体积为144,本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算,属容易题
解析:图为一四棱台和长方体的组合体的三视图,由卷中所给公式计算得体积为144,本题主要考察了对三视图所表达示的空间几何体的识别以及几何体体积的计算,属容易题
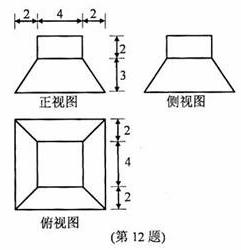
 (2010辽宁文数)(16)如图,网格纸的小正方形的边长是1,在其上用粗线画
(2010辽宁文数)(16)如图,网格纸的小正方形的边长是1,在其上用粗线画
出了某多面体的三视图,则这个多面体最长的一条棱的
长为 .
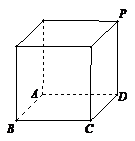 解析:填
解析:填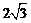 画出直观图:图中四棱锥
画出直观图:图中四棱锥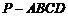 即是,
即是,
所以最长的一条棱的长为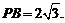
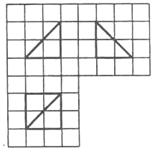 (2010辽宁理数)(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为_____
(2010辽宁理数)(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为_____ _.
_.
[答案]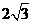
[命题立意]本题考查了三视图视角下 多面体棱长的最值问题,考查了同
多面体棱长的最值问题,考查了同 学们的识图能力以及由三视图还原物体的能力。
学们的识图能力以及由三视图还原物体的能力。
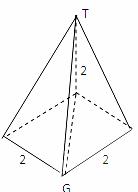
[解析]由三视图可知,此多面体是一个底面边长为2的正方形且有一条长为2的侧棱垂直于底面的四棱锥,所以最长棱长为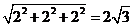
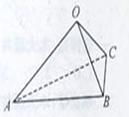 (2010江西理数)16.如图,在三棱锥
(2010江西理数)16.如图,在三棱锥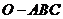 中,三条棱
中,三条棱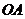 ,
,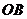 ,
,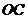 两两垂直,且
两两垂直,且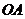 >
>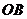 >
>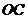 ,分别经过三条棱
,分别经过三条棱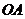 ,
,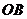 ,
,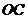 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为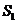 ,
,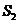 ,
,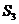 ,则
,则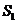 ,
,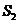 ,
,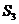 的大小关系为
。
的大小关系为
。
[答案] 
[解析]考查立体图形的空间感和数学知识的运用能力,通过补形,借助长方体验证结论,特殊化,令边长为1,2,3得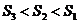 。
。
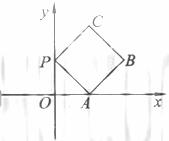
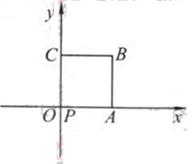 (2010北京文数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
(2010北京文数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的纵坐标与横坐标的函数关系是
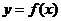 ,则
,则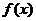 的最小正周期为
;
的最小正周期为
;
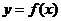 在其两个相邻零点间的图像与x轴
在其两个相邻零点间的图像与x轴
所围区域的面积为 。
说明:“正方形PABC沿x轴滚动”包含沿x轴正方向和沿x轴负方向滚动。沿x轴正方向滚动是指以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续,类似地,正方形PABC可以沿着x轴负方向滚动。
答案:4 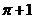
 (2010北京理数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
(2010北京理数)(14)如图放置的边长为1的正方形PABC沿x轴滚动。
设顶点p(x,y)的轨迹方程是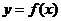 ,则
,则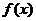 的最小正周期为
;
的最小正周期为
;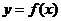 在其两个相邻零点间的图像与x轴所围区域的面积为
在其两个相邻零点间的图像与x轴所围区域的面积为
说明:“正方形PABC沿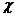 轴滚动”包括沿
轴滚动”包括沿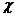 轴正方向和沿
轴正方向和沿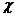 轴负方向
轴负方向 滚动。沿
滚动。沿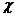 轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在
轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在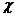 轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿
轴上时,再以顶点B为中心顺时针旋转,如此继续。类似地,正方形PABC可以沿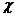 轴负方向滚动。
轴负方向滚动。
答案:4 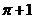
(2010四川理数)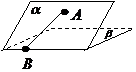 (15)如图,二面角
(15)如图,二面角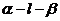 的大小是60°,线段
的大小是60°,线段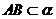 .
.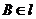 ,
,
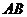 与
与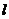 所成的角为30°.则
所成的角为30°.则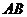 与平面
与平面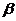 所成的角的正弦值是
.
所成的角的正弦值是
.
解析:过点A作平面β的垂线,垂足为C,在 β内过C作l的垂线.垂足为D
β内过C作l的垂线.垂足为D
连结AD,有三垂线定理可知AD⊥l,
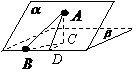 故∠ADC为二面角
故∠ADC为二面角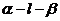 的平面角,为60°
的平面角,为60°
又由已知,∠ABD=30°
连结CB,则∠ABC为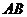 与平面
与平面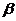 所成的
所成的 角
角
设AD=2,则AC=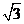 ,CD=1
,CD=1
AB=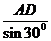 =
= 4
4
∴sin∠ABC=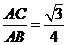
答案: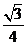
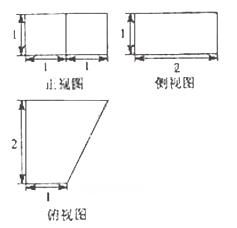 (2010天津文数)(12)一个几何体的三视图如图所示,则这个几何体的体积为
。
(2010天津文数)(12)一个几何体的三视图如图所示,则这个几何体的体积为
。
[答案]3
[解析]本题主要考查三视图的 基础知识,和主题体积的计算,属于容易题。
基础知识,和主题体积的计算,属于容易题。
由俯视图可知该几何体的底面为直角梯形,则正视图和俯视图可知该几何体的高为1,结合三个试图可知该几何体是底面为直角梯形的直四棱柱,所以该几何题的体积为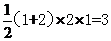
[温馨提示]正视图和侧视图的高是几何体的高,由俯视图可以确定几何体底面的形状,本题也可以将几何体看作是底面是长为3,宽为2,高为1的长方体的一半。
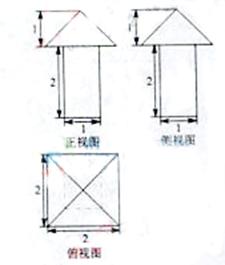 (2010天津理数)(12)一个几何体的三视图如图所示,则这个几何体的体积为
(2010天津理数)(12)一个几何体的三视图如图所示,则这个几何体的体积为
[答案]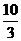
[解析]本题主要考查三视图的概念与柱体、椎体体积的计算,属于容易题。
由三视图可知,该几何体为一个底面边长为1,高为2的正四棱柱与一个 底面边长为2,高为1的正四棱锥组成的组合体,因为正巳灵珠的体积为2,正四棱锥的体积为
底面边长为2,高为1的正四棱锥组成的组合体,因为正巳灵珠的体积为2,正四棱锥的体积为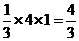 ,所以该几何体的体积V=2+
,所以该几何体的体积V=2+ 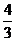 =
= 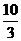
[温馨提示]利用俯视图可以看出几何体底面的形状,结合正视图与侧视图便可得到几何体的形状,求锥体体积时不要丢掉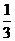 哦。
哦。
(2010四川文数)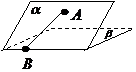 (15)如图,二面角
(15)如图,二面角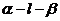 的大小是60°,线段
的大小是60°,线段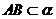 .
.
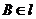 ,
,
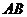 与
与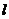 所成的角为30°.则
所成的角为30°.则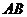 与平面
与平面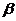 所成的角的正弦值是
.
所成的角的正弦值是
.
解析:过点A作平面β的垂线,垂足为C,在β内过C作l的垂线.垂足为D
连结AD,有三垂线定理可知AD⊥l,
故∠ADC为二面角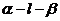 的平面角,为60°
的平面角,为60°
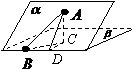 又由
又由 已知,∠ABD=30°
已知,∠ABD=30°
连结CB,则∠ABC为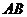 与平
与平 面
面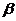 所成的角
所成的角
设AD=2,则AC=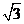 ,CD=1
,CD=1
AB=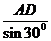 =4
=4
∴sin∠ ABC=
ABC=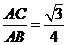
答案: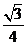

6.(2010上海文数)已知四棱椎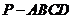 的底面是边长为6 的正方形,侧棱
的底面是边长为6 的正方形,侧棱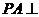 底面
底面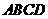 ,且
,且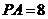 ,则该四棱椎的体积是 96 。
,则该四棱椎的体积是 96 。
解析:考查棱锥体积公式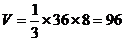
14.(2010湖南文数)若不同两点P,Q的坐标分别为(a,b),(3-b,3-a),则线段PQ的垂直平分线l的斜率为 -1 ,圆(x-2)2+(y-3)2=1关于直线对称的圆的方程为
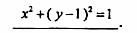
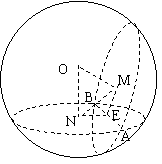
(2010全国卷2理数)(16)已知球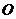 的半径为4,圆
的半径为4,圆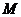 与圆
与圆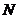 为该球的两个小圆,
为该球的两个小圆,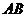 为圆
为圆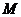 与圆
与圆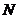 的公共弦,
的公共弦,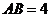 .若
.若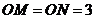 ,则两圆圆心的距离
,则两圆圆心的距离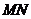
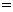 .
.
[答案]3
[命题意图]本试题主要考查球的截面圆的性质,解三角形问题.
[解析]设E为AB的中点,则O,E,M,N四点共面,如图,∵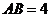 ,所以
,所以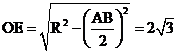 ,∴
,∴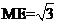 ,由球的截面性质,有
,由球的截面性质,有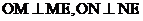 ,∵
,∵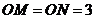 ,所以
,所以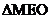 与
与 全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,
全等,所以MN被OE垂直平分,在直角三角形中,由面积相等,可得,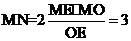
 (2010全国卷2文数)(16)已知球
(2010全国卷2文数)(16)已知球 的半径为4,圆
的半径为4,圆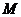 与圆
与圆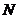 为该球的两个小圆,
为该球的两个小圆,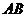 为圆
为圆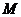 与圆
与圆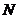 的公共弦,
的公共弦,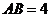 ,若
,若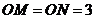 ,则两圆圆心的距离
,则两圆圆心的距离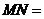 。
。
[解析]3:本题考查球、直线与圆的基础知识
∵ ON=3,球半径为4,∴小圆N的半径为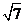 ,∵小圆N中弦长AB=4,作NE垂直于AB,∴ NE=
,∵小圆N中弦长AB=4,作NE垂直于AB,∴ NE=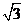 ,同理可得
,同理可得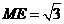 ,在直角三角形ONE中,∵
NE=
,在直角三角形ONE中,∵
NE=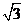 ,ON=3,∴
,ON=3,∴ 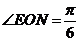 ,∴
,∴ 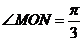 ,∴ MN=3
,∴ MN=3
(2010山东文数)(16) 已知圆C过点(1,0),且圆心在x轴的正半轴上,直线l: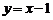 被该圆所截得的弦长为
被该圆所截得的弦长为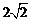 ,则圆C的标准方程为
.
,则圆C的标准方程为
.
4. (2010江苏卷)4、某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的 长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有_▲___根在棉花纤维的长度小于20mm。
长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有_▲___根在棉花纤维的长度小于20mm。
[解析]考查频率分布直方图的知识。
100×(0.001+0.001+0.004)×5=30
3. (2010江苏卷)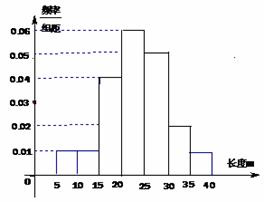 3、盒子中有大小相同的3只白球,1只黑球,若从中随机地摸出两只球,两只球颜色不同的概率是_ ▲__.
3、盒子中有大小相同的3只白球,1只黑球,若从中随机地摸出两只球,两只球颜色不同的概率是_ ▲__.
[解析]考查古典概型知识。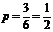
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com