2．从高为5 m处以某一初速度竖直向下抛一小球，在与地面相碰后弹起，上升到高为2 m处被接住，则这段过程中　　　　　　　　　　　　　　　　　　　　　 (　)

A．小球的位移为3 m，方向竖直向下，路程为7 m

B．小球的位移为7 m，方向竖直向下，路程为7 m

C．小球的位移为3 m，方向竖直向下，路程为3 m

D．小球的位移为7 m，方向竖直向下，路程为3 m

解析：路程是标量，是物体运动轨迹的路线长度，s＝5 m+2 m＝7 m；位移是矢量，是由起点指向末点的有向线段，位移方向为起点指向末点，大小为有向线段长度Δx＝3 m，方向竖直向下．A选项正确．

答案：A

1．2008年的奥运圣火经珠穆朗玛峰传至北京，观察图1中的旗帜和甲、乙两火炬手所传递的圣火火焰，关于甲、乙两火炬手相对于静止旗杆的运动情况，下列说法正确的是(旗杆和甲、乙火炬手在同一地区)　　　　　　　　　　　　　　　　 (　)

图1

A．甲、乙两火炬手一定向左运动

B．甲、乙两火炬手一定向右运动

C．甲火炬手可能运动，乙火炬手向右运动

D．甲火炬手可能静止，乙火炬手向左运动

解析：由静止旗杆上旗帜的展向可知，此地区风向向左，火炬甲的火焰向左，甲火炬手可能静止不动，也可能向右运动，还有可能向左运动，但向左运动的速度小于风速，火炬乙的火焰向右，则乙一定向左运动，且向左运动的速度大于风速，故只有D正确．

答案：D

22、(本小题满分10分)

圆χ²+y²=8内有一点P_o(－1，2)，AB为过点P_o且倾斜角为α的弦，

(1)当α=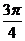时，求AB的长。

(2)当弦AB被点P_o平分时，写出直线AB的方程。

09-10学年度开原高中高二第三次月考考试

21、(本小题满分12分)

已知函数f(χ)= χ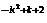(k∈Z)满足f(2)＜f(3)

(1)求k的值并求出相应的f(χ)的解析式。

(2)对于(1)中得到的函数f(χ)，试判断是否存在q，使得g(χ)=1－qf(χ)+(2q－1)χ　　　

在[－1，2]上值域为[－4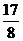，]？若存在，求出q；若不存在，请说明理由。

20、(本小题满分12分)

已知函数f(χ)=χ³+(1－a)χ²－a(a+2)χ +b(a.b∈R)

(1)若函数f(χ)的图象过原点，且在原点处的切线斜率是－3，求a、b的值。

(2)若函数f(χ)在区间(－1，1)上不单调，求a的取值范围。

19、(本小题满分12分)

设f(χ)=cos(2χ+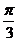)+sin²χ

求(1)求函数f(χ)的最大值和最小正周期

(2)设A, B, C为△ABC的三个内角，若cosB=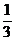, f(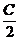)=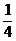－ ，且C为锐角，求sinA。

18、(本小题满分12分)

一台机器使用的时候较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，下表为抽样试验的结果：

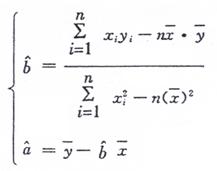
(1)画出散点图，并通过散点图确定变量y对χ是否线性相关；

(2)如果y对χ有线性相关关系，求回归直线方程；

(3)若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么机器的运转速度应控制在什么范围内？(精确到0.0001)

参考公式：线性回归方程的系数公式：

17、(本题满分12分)

已知复数z=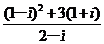 若z²+az+b=1－i

(1)求z;

(2)求实数a、b的值.

16、Rt△ABC中，∠CAB=90度，AD⊥BC于D，AB:AC=3:2，则CD:BD=_____________

15、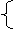曲线C： χ=cosθ　　　 (θ为参数，且0≤θ≤π)的普通方程为　　　　　　　 ，

y=－1+sinθ　 　

如果曲线C与直线χ+y+a=0有公共点，那么a的取值范围是