
9.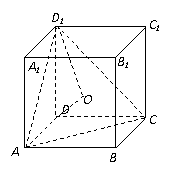 D [命题意图]本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面AC
D [命题意图]本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法,利用等体积转化求出D到平面AC 的距离是解决本题的关键所在,这也是转化思想的具体体现.
的距离是解决本题的关键所在,这也是转化思想的具体体现.
[解析1]因为BB1//DD1,所以B 与平面AC
与平面AC 所成角和DD1与平面AC
所成角和DD1与平面AC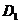 所成角相等,设DO⊥平面AC
所成角相等,设DO⊥平面AC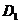 ,由等体积法得
,由等体积法得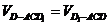 ,即
,即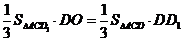 .设DD1=a,
.设DD1=a,
则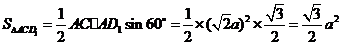 ,
,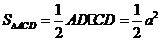 .
.
所以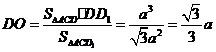 ,记DD1与平面AC
,记DD1与平面AC 所成角为
所成角为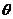 ,则
,则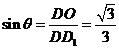 ,所以
,所以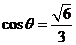 .
.
[解析2]设上下底面的中心分别为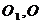 ;
;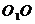 与平面AC
与平面AC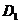 所成角就是B
所成角就是B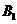 与平面AC
与平面AC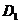 所成角,
所成角,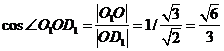
(2010全国卷1文数)(6)直三棱柱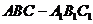 中,若
中,若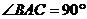 ,
,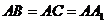 ,则异面直线
,则异面直线
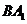 与
与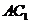 所成的角等于
所成的角等于
(A)30° (B)45°(C)60° (D)90°
12.B[命题意图]本小题主要考查几何体的体积的计算、球的性质、异面直线的 距离,通过球这个载体考查考生的空间想象能力及推理运算能力.
距离,通过球这个载体考查考生的空间想象能力及推理运算能力.
[解析]过CD作平面PCD,使AB⊥平面PCD,交AB与P,设点P到CD的距离为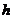 ,则有
,则有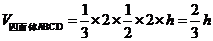 ,当直径通过AB与CD的中点时,
,当直径通过AB与CD的中点时,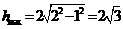 ,故
,故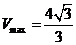
(2010全国卷1文数)(9)正方体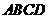 -
-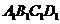 中,
中,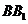 与平面
与平面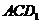 所成角的余弦值为
所成角的余弦值为
(A) 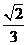 (B)
(B)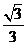 (C)
(C)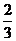 (D)
(D)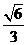
6.D.
(2010广东文数)
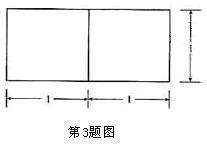 (2010福建文数)3.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )
(2010福建文数)3.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )
A.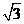 B.2
B.2
C.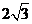 D.6
D.6
[答案]D
[解析]由正视图知:三棱柱是以底面边长为2,高为1的正三棱柱,所以底面积为
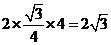 ,侧面积为
,侧面积为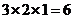 ,选D.
,选D.
[命题意图]本题考查立体几何中的三视图,考查同学们识图的能力、空间想象能力等基本能力。
(2010全国卷1文数)(12)已知在半径为2的球面上有A、B、C、D四点,若AB=CD=2,则四面体ABCD的体积的最大值为
(A) 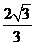 (B)
(B)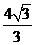 (C)
(C) 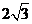 (D)
(D) 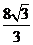
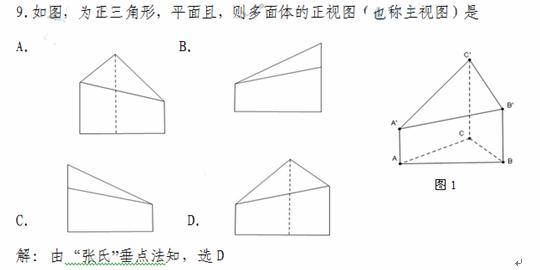
6.(2010广东理数)如图1,△ ABC为三角形,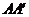 //
//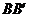 //
//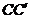 ,
, 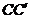 ⊥平面ABC 且3
⊥平面ABC 且3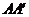 =
=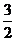
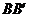 =
=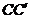 =AB,则多面体△ABC -
=AB,则多面体△ABC -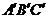 的正视图(也称主视图)是
的正视图(也称主视图)是
9.B
[解析]该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和。
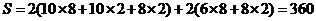 .
.
[方法技巧]把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体,画出直观图,得出各个棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
(2010重庆文数)(9)到两互相垂直的异面直线的距离相等的点
(A)只有1个 (B)恰有3个
(C)恰有4个 (D)有无穷多个
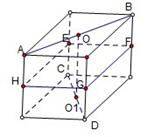 解析:放在正方体中研究,显然,线段
解析:放在正方体中研究,显然,线段 、EF、FG、GH、
、EF、FG、GH、
HE的中点到两垂直异面直线AB、CD的距离都相等,
所以排除A、B、C,选D
亦可在四条侧棱上找到四个点到两垂直异面直线AB、CD的距离相等
 (2010浙江文数)
(2010浙江文数)
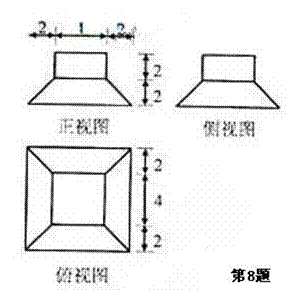
(8)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是
(A)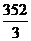 cm3
cm3
(B)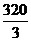 cm3
cm3
(C)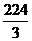 cm3
cm3
(D)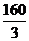 cm3
cm3
解析:选B,本题主要考察了对三视图所表达示的空间几何体的识别以及几 何体体积的计算,属容易题
何体体积的计算,属容易题
(2010山东文数)(4)在空间,下列命题正确的是
A.平行直线的平行投影重合
B.平行于同一直线的两个平面平 行
行
C.垂直于同一平面的两个平面平行
D.垂直于同一平面的两条直线平行
答案:D
 (201
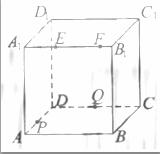
(201 0北京文数)(8)如图,正方体
0北京文数)(8)如图,正方体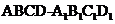 的棱长为2,
的棱长为2,
动点E、F在棱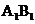 上。点Q是CD的中点,动点
上。点Q是CD的中点,动点
P在棱AD上,若EF=1,DP=x,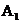 E=y(x,y大于零),
E=y(x,y大于零),
则三棱锥P-EFQ的体积:
(A)与x,y都有关; (B)与x,y都无关;
(C)与x有关,与y无关; (D)与y有关,与x无关;
答案:C
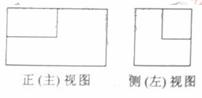
(2010北京文数)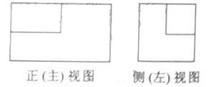 (5)一个长方体去掉一个小长方体,所得几何体的
(5)一个长方体去掉一个小长方体,所得几何体的
正(主)视图与侧(左)视图分别如右图所示,则该
集合体的俯视图为:
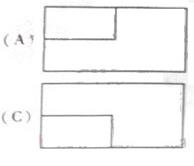

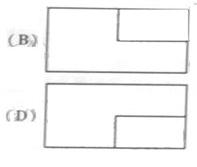
答案:C
 (201
(201 0北京理数)(8)如图,正方体ABCD-
0北京理数)(8)如图,正方体ABCD- 的棱长为2,动点E、F在棱
的棱长为2,动点E、F在棱 上,动点P,Q分别在棱AD,CD上,若EF=1,
上,动点P,Q分别在棱AD,CD上,若EF=1, E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
E=x,DQ=y,DP=z(x,y,z大于零),则四面体PEFQ的体积
(A)与x,y,z都有关
(B)与x有关,与y,z无关
(C)与y有关,与x,z无关
(D)与z有关,与x,y无关
答案:D
 (2010北京理数)(3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为
(2010北京理数)(3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为
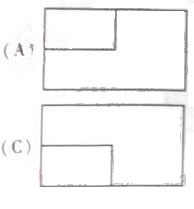
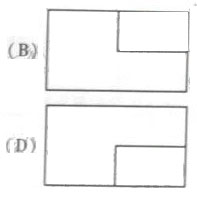
答案:C
(2010四川理数)(11)半径为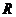 的球
的球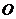 的直径
的直径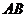 垂直于平面
垂直于平面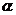 ,垂足为
,垂足为 ,
,
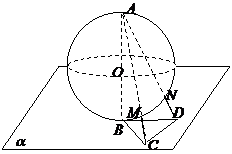
 是平面
是平面 内边长为
内边长为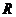 的正三角形,线段
的正三角形,线段
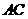 、
、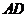 分别
分别
与球面交于点M,N,那么M、N两点 间的球面距离是
间的球面距离是
(A)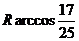 (B)
(B)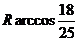
(C)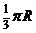 (D)
(D)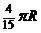
解析:由已知,AB=2R,BC=R,故tan∠BAC=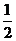
cos∠BAC=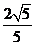
连结OM,则△OAM为等腰三角形
AM=2AOcos∠BAC=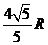 ,同理AN=
,同理AN=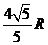 ,且MN∥CD
,且MN∥CD
而AC=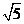 R,CD=R
R,CD=R
故MN:CD=AN:AC
Þ MN=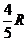 ,
,
连结OM、ON,有OM=ON=R
于是cos∠MON=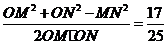
所以M、N两点间的球面距离是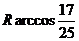
答案:A
2. (山东卷理7)由曲线
(山东卷理7)由曲线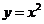 ,
,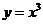 围城的封闭图形面积为
围城的封闭图形面积为
(A) 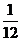 (B)
(B)
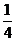 (C)
(C) 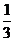 (D)
(D) 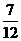
[答案]A
[解析]由题意得:所求封闭图形的面积为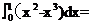
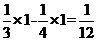 ,故选A。
,故选A。
[命题意图]本题考查定积分的基础知识,由定积分求曲线围成封闭图形的面积。
1.(湖南卷理5)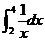 等于
等于
A、 B、
B、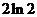 C、
C、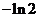 D、
D、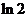
9.D
[解析]画出图形,设动点A与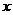 轴正方向夹角为
轴正方向夹角为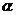 ,则
,则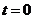 时
时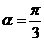 ,每秒钟旋转
,每秒钟旋转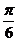 ,在
,在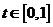 上
上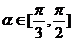 ,在
,在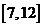 上
上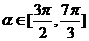 ,动点
,动点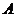 的纵坐标
的纵坐标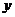 关于
关于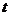 都是单调递增的。
都是单调递增的。
[方法技巧]由动点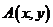 在圆
在圆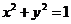 上绕坐标原点沿逆时针方向匀速旋转,可知与三角函数的定义类似,由12秒旋转一周能求每秒钟所转的弧度,画出单位圆,很容易看出,当t在
上绕坐标原点沿逆时针方向匀速旋转,可知与三角函数的定义类似,由12秒旋转一周能求每秒钟所转的弧度,画出单位圆,很容易看出,当t在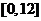 变化时,点
变化时,点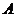 的纵坐标
的纵坐标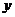 关于
关于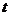 (单位:秒)的函数的单调性的变化,从而得单调递增区间.
(单位:秒)的函数的单调性的变化,从而得单调递增区间.
1. (2010安徽理数)9、动点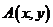 在圆
在圆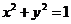 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间
上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周。已知时间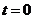 时,点
时,点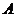 的坐标是
的坐标是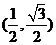 ,则当
,则当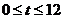 时,动点
时,动点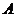 的纵坐标
的纵坐标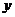 关于
关于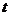 (单位:秒)的函数的单调递增区间是
(单位:秒)的函数的单调递增区间是
A、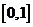 B、
B、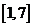 C、
C、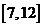 D、
D、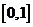 和
和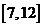
4.A
[解析]设直线方程为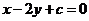 ,又经过
,又经过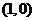 ,故
,故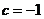 ,所求方程为
,所求方程为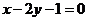 .
.
[方法技巧]因为所求直线与与直线x-2y-2=0平行,所以设平行直线系方程为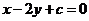 ,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
(2010重庆文数)(8)若直线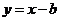 与曲线
与曲线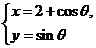 (
(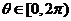 )有两个不同的公共点,则实数
)有两个不同的公共点,则实数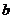 的取值范围为
的取值范围为
(A)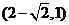 (B)
(B)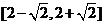
 (C)
(C)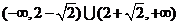 (D)
(D)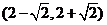
解析: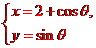 化为普通方程
化为普通方程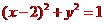 ,表示圆,
,表示圆,
因为直线与圆有两个不同的交点,所以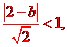 解得
解得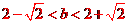
法2:利用数形结合进行分析得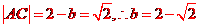
同理分析,可知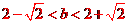
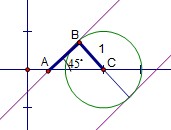
(2010重庆理数)(8) 直线y=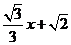 与圆心为D的圆
与圆心为D的圆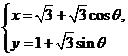
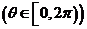 交与A、B两点,则直线AD与BD的倾斜角之和为
交与A、B两点,则直线AD与BD的倾斜角之和为
 A.
A. 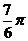 B.
B. 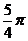 C.
C. 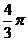 D.
D. 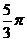
解析:数形结合
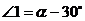
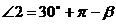
由圆的性质可知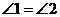
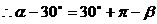
故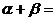
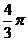
(2010广东文数)

(2010全国卷1理数)(11)已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么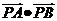 的最小值为
的最小值为
(A) 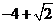 (B)
(B)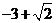 (C)
(C) 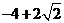 (D)
(D)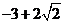

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com