
5、由绝对值的定义引发的讨论
例8.(2008山东省郓城一中)已知等比数列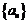 中,
中,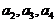 分别是某等差数列的第5项,第3项,第2项,且
分别是某等差数列的第5项,第3项,第2项,且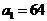 ,公比
,公比 ;
;
(1)求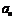 (2)设
(2)设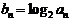 ,求数列
,求数列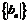 的前n项和
的前n项和 。
。
分析:由已知条件求得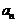 ,从而得到
,从而得到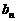 ,在求数列
,在求数列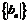 的前n项和
的前n项和 时,要根据绝对值的定义将绝对值的符号去掉,再求和。
时,要根据绝对值的定义将绝对值的符号去掉,再求和。
解:(Ⅰ)依题意得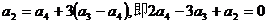
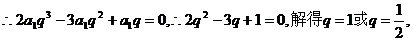
又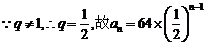
(Ⅱ)
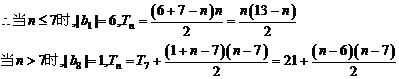
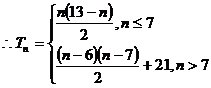
评注:本题为由绝对值的定义引发的分类讨论,注意最后要整合所求的答案。即用分段函数表示出数列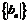 的前n项和
的前n项和 的解析式。
的解析式。
例9.(2008江苏卷20)已知函数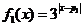 ,
,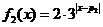 (
(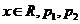 为常数).函数
为常数).函数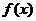 定义为:对每个给定的实数
定义为:对每个给定的实数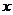 ,
,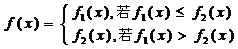
(1)求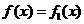 对所有实数
对所有实数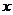 成立的充分必要条件(用
成立的充分必要条件(用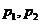 表示);
表示);
(2)设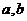 是两个实数,满足
是两个实数,满足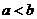 ,且
,且 .若
.若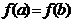 ,求证:函数
,求证:函数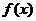 在区间
在区间 上的单调增区间的长度之和为
上的单调增区间的长度之和为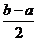 (闭区间
(闭区间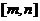 的长度定义为
的长度定义为 )
)
分析:由于题目所给的条件就是分段函数,注意到其使用的前提条件,就可以进行转化,根据(1)的结论在解答(2)时,就要注意满足和不满足(1)的结论,从而选择具体使用哪一个解析式,并进行分类讨论。
解:(1)由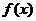 的定义可知,
的定义可知,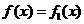 (对所有实数
(对所有实数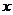 )等价于
)等价于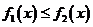 (对所有实数
(对所有实数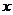 )这又等价于
)这又等价于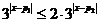 ,即
,即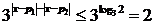 对所有实数
对所有实数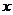 均成立. (*) 由于
均成立. (*) 由于 的最大值为
的最大值为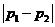 ,
,
故(*)等价于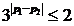 ,即
,即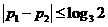 ,这就是所求的充分必要条件。
,这就是所求的充分必要条件。
(2)分两种情形讨论
(i)当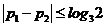 时,由(1)知
时,由(1)知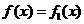 (对所有实数
(对所有实数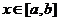 )
)
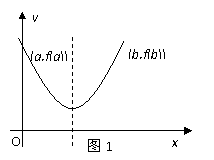 则由
则由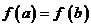 及
及 易知
易知 ,
,
再由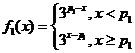 的单调性可知,
的单调性可知,
函数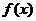 在区间
在区间 上的单调增区间的长度
上的单调增区间的长度
为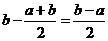 (参见示意图1)
(参见示意图1)
(ii)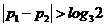 时,不妨设
时,不妨设 ,则
,则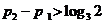 ,于是
,于是
当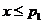 时,有
时,有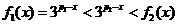 ,从而
,从而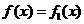 ;
;
当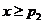 时,有
时,有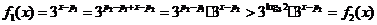
 从而
从而
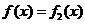 ;当
;当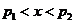 时,
时,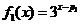 ,及
,及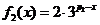 ,由方程
,由方程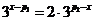 解得
解得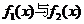 图象交点的横坐标为
图象交点的横坐标为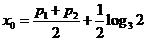 ⑴
⑴
显然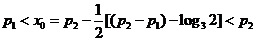 ,
,
这表明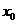 在
在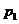 与
与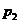 之间。由⑴易知
之间。由⑴易知 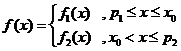
综上可知,在区间 上,
上,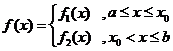 (参见示意图2)
(参见示意图2)
故由函数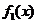 及
及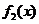 的单调性可知,
的单调性可知,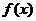 在区间
在区间 上的单调增区间的长度之和为
上的单调增区间的长度之和为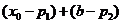 ,由于
,由于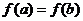 ,即
,即 ,得
,得
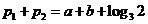 ⑵
⑵
故由⑴、⑵得 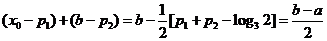
综合(i)(ii)可知,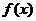 在区间
在区间 上的单调增区间的长度和为
上的单调增区间的长度和为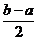 。
。
评注:本题的条件比较复杂,题目中解析式需要自己根据条件确定,进行分类讨论。解决本题的障碍在于有可能读不懂题意,条件比较抽象,从而对问题的转化产生障碍,不能够做到善始善终地解决彻底。
4、两个实数大小关系的确定
例6.(2008宁夏银川一中)设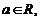 且
且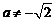 ,比较
,比较 与
与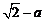 的大小.
的大小.
分析:用作差法比较两个实数的大小,当情况不定时需要分类讨论。
解: 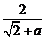 -(
-(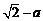 )=
)=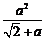 ,
,
当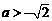 且
且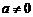 时,∵
时,∵ 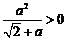 ,∴
,∴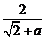
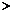
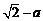 .
.
当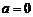 时, ∵
时, ∵ 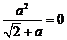 ,∴
,∴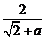 =
=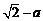 .
.
当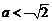 时,∵
时,∵ 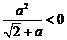 ,∴
,∴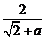
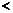
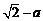 。
。
评注:在比较两个数的大小关系时,要注意参数的取值范围和不同的取值所得到的结果不同。
例7.(2008南通四县)已知函数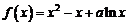
(1)当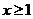 时,
时,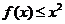 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)讨论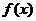 在定义域上的单调性;
在定义域上的单调性;
分析:(1)中不等式恒成立问题可以分离出参数 ,但在分离过程中,由于
,但在分离过程中,由于 的系数的不同取值会产生分类讨论,分别转化为函数研究最值,(2)在利用导数研究函数的单调性时,由于导函数值为0时的根不定而引发分类讨论。
的系数的不同取值会产生分类讨论,分别转化为函数研究最值,(2)在利用导数研究函数的单调性时,由于导函数值为0时的根不定而引发分类讨论。
解:(1):由 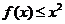 恒成立,得:
恒成立,得: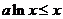 在
在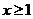 时恒成立
时恒成立
当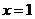 时
时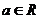 ,当
,当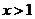 时即
时即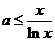 ,令
,令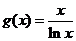 ,
,
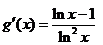
由于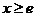 时
时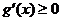 ,
,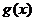 在
在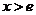 时为增函数,
时为增函数,
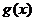 在
在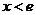 时为减函数
时为减函数
∴ 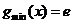 ∴
∴ 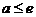
(2):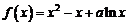 ,
,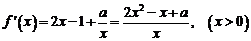
(Ⅰ)当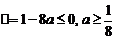 时,
时,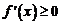 恒成立,
恒成立,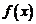 在
在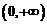 上为增函数.
上为增函数.
(Ⅱ)当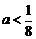 时,①当
时,①当 时,
时,
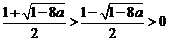 ,
,
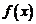 在
在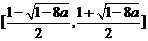 上为减函数,
上为减函数,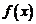 在
在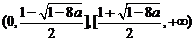 上为增函数。②当
上为增函数。②当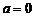 时,
时,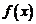 在
在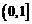 上为减函数,
上为减函数,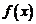 在
在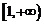 上为增函数.
上为增函数.
③当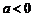 时,
时,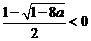 ,故
,故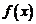 在
在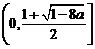 ]上为减函数,
]上为减函数,
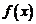 在[
在[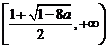 上为增函数.
上为增函数.
评注:在进行分类讨论时,要注意分类的标准的划分,做到不重不漏。.
3、变量对不等式变形的影响
例5.(2008江苏卷14).设函数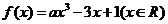 ,若对于任意的
,若对于任意的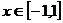 都有
都有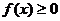 成立,则实数
成立,则实数 的值为
的值为
分析:若对于任意的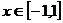 都有
都有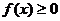 成立,不等式恒成立求参数的范围,可将参数
成立,不等式恒成立求参数的范围,可将参数 分化出来,在分离
分化出来,在分离 时需要对其系数
时需要对其系数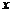 的正负进行讨论,转为
的正负进行讨论,转为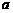 的不等式,然后可以通过求导研究右边关于
的不等式,然后可以通过求导研究右边关于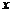 的函数,判断其单调性并求出其最值。
的函数,判断其单调性并求出其最值。
解:若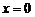 ,则不论
,则不论 取何值,
取何值,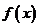 ≥0显然成立;当
≥0显然成立;当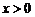 即
即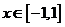 时,
时, ≥0可化为:
≥0可化为: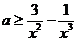
设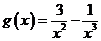 ,则
,则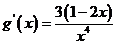 ,
所以
,
所以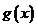 在区间
在区间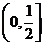 上单调递增,在区间
上单调递增,在区间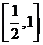 上单调递减,因此
上单调递减,因此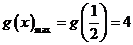 ,从而
,从而 ≥4;
≥4;
当x<0 即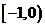 时,
时, ≥0可化为
≥0可化为
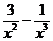 ,
,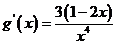

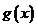 在区间
在区间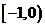 上单调递增,因此
上单调递增,因此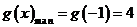 ,从而
,从而 ≤4,综上
≤4,综上 =4
=4
答案:4
评注:本小题考查不等式的转化和函数单调性的综合运用。对于不等式恒成立问题常常要将参数分离出来,转化为研究函数的最值。通过求导研究函数的单调性和最值,在情况不定时对其取值进行分类讨论。
2、函数的零点(或方程的根)与所给区间关系的讨论
例3.(2007广东) 已知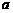 是实数,函数
是实数,函数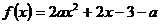 ,如果函数
,如果函数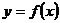 在区间
在区间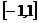 上有零点,求
上有零点,求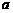 的取值范围.
的取值范围.
分析:先确定函数的类型,函数的零点即为方程的根,对于二次方程的实根情况要结合其对称轴和区间进行分类讨论。
解:若 ,
, 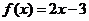 ,显然在
,显然在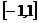 上没有零点, 所以
上没有零点, 所以 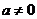 .
.
令  , 解得
, 解得 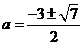
①当 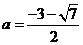 时,
时, 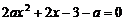 的解为
的解为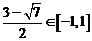 ,
,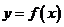 恰有一个零点在
恰有一个零点在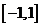 上;
上;
②当 ,即
,即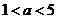 时,
时,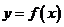 在
在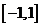 上也恰有一个零点.
上也恰有一个零点.
③当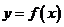 在
在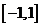 上有两个零点时, 则
上有两个零点时, 则
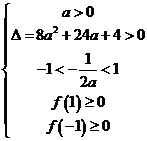 或
或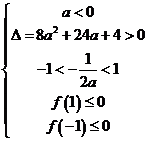
解得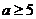 或
或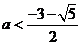 ,综上所求实数
,综上所求实数 的取值范围是
的取值范围是 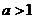 或
或 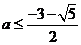 .
.
评注:二次方程的实根分布要结合二次函数的图象对其所给的区间与其对称轴之间的相对位置关系进行分类讨论,可从四个角度考虑①开口方向②对称轴③判别式④端点。
例4.(2008天津卷,文21)已知 是实数,函数
是实数,函数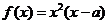 。
。
(Ⅰ)若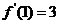 ,求
,求 的值及曲线
的值及曲线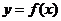 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求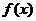 在区间
在区间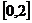 上的最大值。
上的最大值。
分析:本题为三次函数在闭区间上研究最大,可以通过求导,其导函数含有参数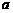 ,在求解方程时,方程的根与区间的位置关系不定而引发的分类讨论。
,在求解方程时,方程的根与区间的位置关系不定而引发的分类讨论。
解:(Ⅰ)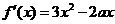 ,因为
,因为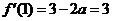 ,所以
,所以 .又当
.又当 时,
时,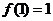 ,
,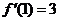 ,所以曲线
,所以曲线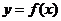 在
在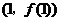 处的切线方程为
处的切线方程为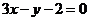 .
.
(Ⅱ)令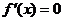 ,解得
,解得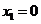 ,
,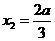 .
.
当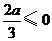 ,即
,即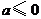 时,
时,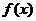 在
在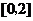 上单调递增,从而
上单调递增,从而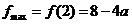 .
.
当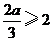 ,即
,即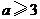 时,
时,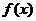 在
在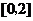 上单调递减,从而
上单调递减,从而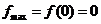 .
.
当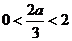 ,即
,即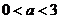 时,
时,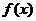 在
在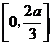 上单调递减,在
上单调递减,在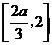 上单调递增,从而
上单调递增,从而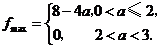 综上所述,
综上所述, 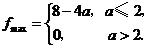
评注:本题主要考查函数的基本性质、导数的应用等基础知识,以及运用分类整合的数学思想和综合运用所学知识分析问题和解决问题的能力.
1、方程、不等式、函数的类型的确定
例1.(山东文登三中2009)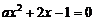 至少有一个正的实根的充要条件是 ( )
至少有一个正的实根的充要条件是 ( )
A.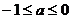 B.
B.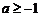 C.
C.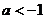 D.
D.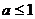
分析:先确定方程的类型,需要按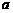 的取值分类,对于二次方程研究根的情况,一般要转化为二次函数和二次不等式(组)解出。
的取值分类,对于二次方程研究根的情况,一般要转化为二次函数和二次不等式(组)解出。
解:当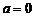 时,方程为
时,方程为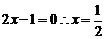 ,满足。当
,满足。当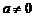 时,
时,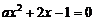 至少有一个正的实根,设
至少有一个正的实根,设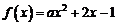 ,当
,当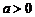 时,∵
时,∵ ,∴
,∴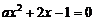 一定有一个正的实根;当
一定有一个正的实根;当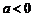 时,∵
时,∵ ,∴
,∴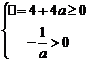 即
即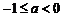 ,综上
,综上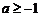 ,故选B
,故选B
答案:B
评注:对于函数、方程、不等式问题,要先判断其类型,而对于二次函数、二次方程、二次不等式之间常常相互转化,并借助函数的图象,得到方程或不等式(组)解出。
例2.(2008山东省泰安市)已知函数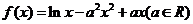 .
.
(1)当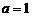 时,证明函数
时,证明函数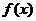 只有一个零点;
只有一个零点;
(2)若函数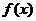 在区间
在区间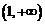 上是减函数,求实数
上是减函数,求实数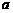 的取值范围.
的取值范围.
分析:要证此类函数只有一个零点,就要通过求导,研究函数的单调性,求导后由于函数中含有参数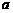 ,那么它的导数要与参数
,那么它的导数要与参数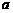 的取值有关,所以单调性的判断要随参数
的取值有关,所以单调性的判断要随参数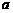 的变化而变化,需要对其去值进行分类讨论。
的变化而变化,需要对其去值进行分类讨论。
解:(1)当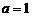 时,
时,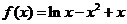 ,其定义域是
,其定义域是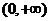 ,
,
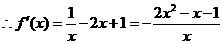 令
令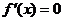 ,即
,即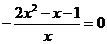 ,
,
解得 或
或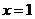 .
. 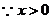 ,
,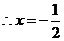 舍去.
舍去.
当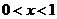 时,
时,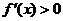 ;当
;当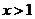 时,
时,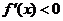 .
.
∴函数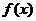 在区间
在区间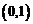 上单调递增,在区间
上单调递增,在区间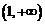 上单调递减
上单调递减
∴当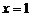 时,函数
时,函数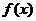 取得最大值,其值为
取得最大值,其值为 .
.
当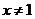 时,
时,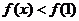 ,即
,即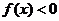 . ∴函数
. ∴函数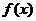 只有一个零点.
只有一个零点.
(2)法一:因为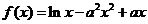 其定义域为
其定义域为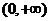 ,
,
 所以
所以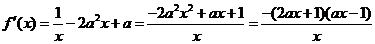
①当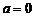 时,
时,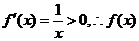 在区间
在区间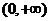 上为增函数,不合题意
上为增函数,不合题意
②当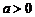 时,
时,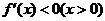 等价于
等价于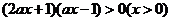 ,即
,即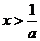 .
.
此时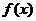 的单调递减区间为
的单调递减区间为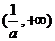 .依题意,得
.依题意,得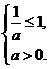 解之得
解之得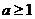 .
.
③当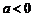 时,
时,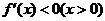 等价于
等价于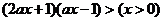 ,即
,即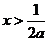 ·
·
此时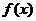 的单调递减区间为
的单调递减区间为 ,
,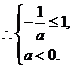 得
得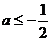
综上,实数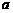 的取值范围是
的取值范围是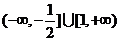
法二: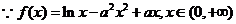
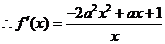
由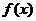 在区间
在区间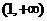 上是减函数,可得
上是减函数,可得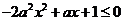 在区间
在区间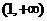 上恒成立.
上恒成立.
① 当 时,
时,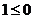 不合题意
不合题意
② 当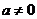 时,可得
时,可得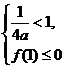 即
即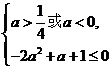
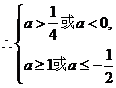
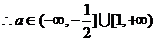
评注:对于函数、不等式、方程的类型不确定时,就要对其参数进行讨论。而对于二次不等式恒成立问题可以借助的图象进行分类转化。
8.预测题
(1).(原创)向量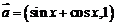 ,
,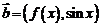 ,其中
,其中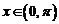 ,
,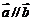 ,则函数
,则函数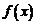 的值域为( )
的值域为( )
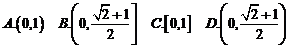
分析:先由已知求出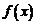 的解析式,再由定义域结合函数的图象求出值域
的解析式,再由定义域结合函数的图象求出值域
解:∵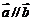 ,
,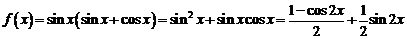
 ,∵
,∵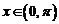 ∴选
∴选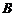
评注:求函数的值域一定要在函数的定义域内结合函数的图象和性质解决。
(2).(原创)已知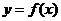 是顶点在原点的二次函数,且方程
是顶点在原点的二次函数,且方程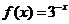 有一个根
有一个根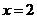 ,则不等式
,则不等式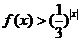 的解集是(
)
的解集是(
)
A.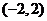 B.
B.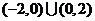 C.
C.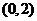 D.
D.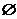
分析:可以根据函数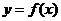 的图象和对称性,以及函数
的图象和对称性,以及函数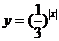 的图象和对称性解答问题。
的图象和对称性解答问题。
解:已知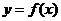 是顶点在原点的二次函数知其图象关于原点对称,又
是顶点在原点的二次函数知其图象关于原点对称,又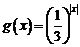 为偶函数,其图象也关于原点对称,又方程
为偶函数,其图象也关于原点对称,又方程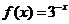 即
即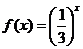 有一个根
有一个根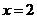 ,所以不等式
,所以不等式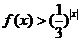 的解集是
的解集是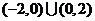 ,故选B
,故选B
评注:在解决函数问题时,要结合函数的图象和性质解答问题。
(3).(原创)当 时,不等式
时,不等式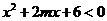 恒成立,则
恒成立,则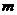 的取值范围是
的取值范围是
分析:不等式、方程、函数可以相互转化,可以通过构造函数,借助函数的图象来解答。
解:构造函数: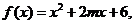
 .由于当
.由于当 时,不等式
时,不等式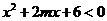 恒成立,等价于在区间
恒成立,等价于在区间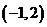 上函数
上函数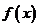 的图象位于
的图象位于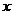 轴下方,由于函数
轴下方,由于函数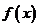 的图象是开口向上的抛物线,故只需
的图象是开口向上的抛物线,故只需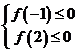 即
即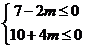 ,解得
,解得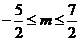 .
.
评注:结合函数图象,根据题目的要求列出参数所满足的条件是解决这类问题的另一个有效方法.特别是对参数以外的另一个变量是一次的情况,这个方法更有效.
(4).(原创) 正方体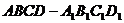 棱长为1,
棱长为1,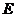 为棱
为棱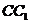 上的动点.
上的动点.
⑴求证: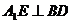 ;
;
⑵当点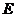 为棱
为棱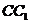 上的中点时,求证:平面
上的中点时,求证:平面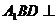 平面
平面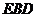 ;
;
⑶在棱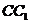 上是否存在一点
上是否存在一点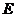 ,使二面角
,使二面角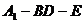 的大小为
的大小为 ?若存在,确定其位置,若不存在,说明理由.
?若存在,确定其位置,若不存在,说明理由.
 分析:利用有关垂直的判定定理判定,在此基础上解决(3),可以设为
分析:利用有关垂直的判定定理判定,在此基础上解决(3),可以设为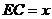 ,求的
,求的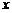 的方程解出。
的方程解出。
证明:⑴连结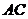 ,则
,则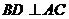 ,
,
∵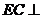 平面
平面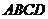 ,
,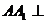 平面
平面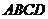 ,
,
∴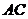 是
是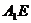 在平面
在平面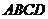 的上的射影,由三垂线定理知,
的上的射影,由三垂线定理知,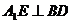 .
.
⑵设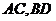 交于点O,连结
交于点O,连结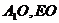 ,
,
∵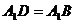 ,∴
,∴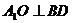 ,同理可证
,同理可证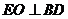 ,
,
∴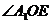 是二面角
是二面角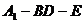 的平面角.
的平面角.
∵正方体棱长为1,∴ ,
,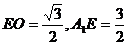 ,∴
,∴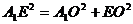 ,
,
∴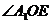
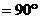 ,∴平面
,∴平面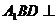 平面
平面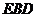 .
.
⑶(理科做)假设在棱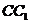 上存在一点
上存在一点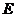 ,使二面角
,使二面角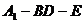 的大小为
的大小为 ,
,
由⑵知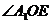
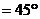 .设
.设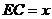 ,则
,则
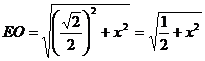 ,
,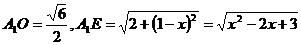 ,
,
∴在 中,由余弦定理得:
中,由余弦定理得: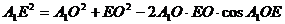 ,
,
∴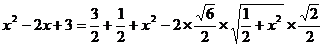 ,可化为
,可化为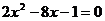 ,
,
解得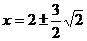 ,由于
,由于
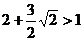 ,
,
∴在棱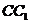 上不存在满足条件的点
上不存在满足条件的点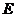 .(说明:理科学生也可用空间向量解决此题.)
.(说明:理科学生也可用空间向量解决此题.)
评注:在确定点的位置时,可以先设出,再解方程求出。
(5).(原创)在直线 :
: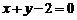 上任取一点M,使过M且以双曲线
上任取一点M,使过M且以双曲线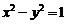 的焦点为焦点的椭圆C的长轴最短
的焦点为焦点的椭圆C的长轴最短
(1)求椭圆C的方程
(2)若一直线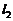 :
: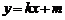 与椭圆C相交于A、B两点(A、B不是椭圆的顶点),以
与椭圆C相交于A、B两点(A、B不是椭圆的顶点),以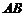 为直径的圆过椭圆的上顶点,求证:直线
为直径的圆过椭圆的上顶点,求证:直线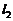 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
分析:由已知条件判断出所求的椭圆的方程形式,再根据图形和椭圆的定义解决定量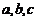 的值,从而求得椭圆方程,并通过解方程组研究直线与椭圆的位置关系, 以
的值,从而求得椭圆方程,并通过解方程组研究直线与椭圆的位置关系, 以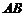 为直径的圆过椭圆的上顶点,说明有互相垂直的关系,从而由韦达定理解答问题即可.
为直径的圆过椭圆的上顶点,说明有互相垂直的关系,从而由韦达定理解答问题即可.
解:(1)∵双曲线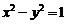 的焦点为
的焦点为 ,∴椭圆C的焦点为
,∴椭圆C的焦点为 ,设椭圆的方程为
,设椭圆的方程为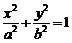 ,
,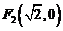 关于直线
关于直线 :
: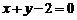 的对称点为
的对称点为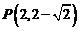 ,连接
,连接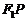 交直线
交直线 :
: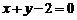 于点M,则
于点M,则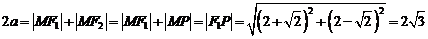 ,∴
,∴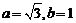 ∴椭圆的方程为
∴椭圆的方程为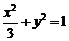 ,椭圆的上顶点为
,椭圆的上顶点为
(2)由方程组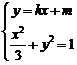 得
得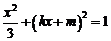 ,即
,即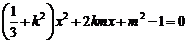 ,
,
△=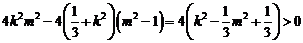 ,即
,即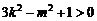 ,
,
设A、B两点的坐标分别为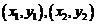 ,则
,则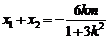 ,
,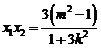 ,
,
∴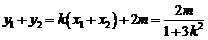 ,
,
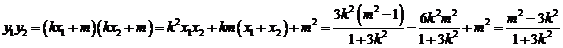 ∵以
∵以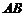 为直径的圆过椭圆的上顶点
为直径的圆过椭圆的上顶点 ,∴
,∴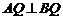 ∴
∴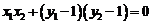 ,
,
即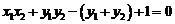 ,∴
,∴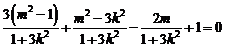 ,化简得
,化简得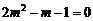 ,∴
,∴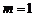 或
或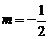 .当
.当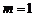 时,直线
时,直线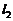 :
: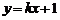 过定点
过定点 与已知矛盾. 当
与已知矛盾. 当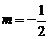 时, 满足
时, 满足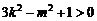 ,此时直线
,此时直线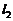 为:
为: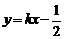 过定点
过定点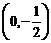 ,∴直线
,∴直线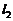 过定点
过定点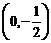 .
.
评注:解决圆锥曲线问题,要注重圆锥曲线的基础知识的考查, 从定义、标准方程、性质,到直线与圆锥曲线位置关系的讨论,做到熟悉常规解法,要注重数形结合的思想和解方程的思想的渗透.要求思维要严密,运算精湛.
(6) (2008年潍坊市,改编)定义在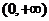 的两个函数
的两个函数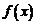 和
和 ,已知
,已知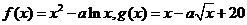 ,且
,且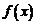 在
在 处取极值.
处取极值.
(I)求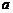 的值及
的值及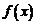 和
和 的单调区间;
的单调区间;
(Ⅱ)求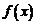 和
和 的图象的交点个数,并说明道理.(其中
的图象的交点个数,并说明道理.(其中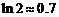 )
)
分析: 由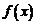 在
在 处取极值,可求得
处取极值,可求得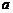 的值,,求导确定其单调区间,(3)可构造函数由函数的单调性研究方程的解,即曲线的交点.
的值,,求导确定其单调区间,(3)可构造函数由函数的单调性研究方程的解,即曲线的交点.
解(Ⅰ)由题意: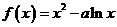 ,∴
,∴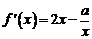 ,∵
,∵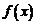 在
在 处取极值.
处取极值.
∴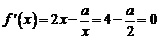 ∴
∴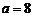 …………………………………………… 2分
…………………………………………… 2分
∴ ∴
∴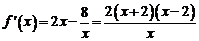
∵定义域为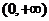 ,∴当
,∴当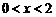 时,
时,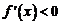 ,
, 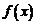 为减函数;
为减函数;
当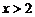 时,
时, 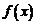 为增函数. ∴
为增函数. ∴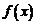 的减区间为
的减区间为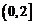 , 增区间为
, 增区间为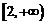 .………4分
.………4分
而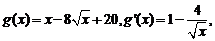
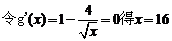 .
.
当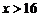 时,
时, 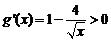 ∴
∴ 在
在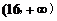 上为增函数;
上为增函数;
当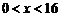 时,
时, , ∴
, ∴ 在
在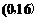 上为减函数.
上为减函数.
∴ 的减区间为
的减区间为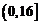 , 增区间为
, 增区间为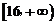
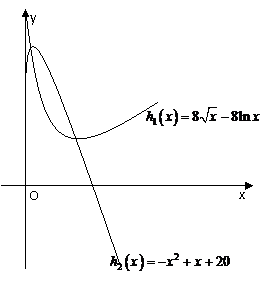 (Ⅱ)
(Ⅱ) 与
与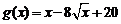 的图象的交点个数,
的图象的交点个数,
即求方程: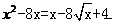
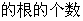
即: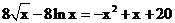 ,设
,设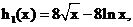
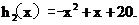
则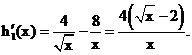
∴当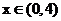 时,
时, 为减函数.
为减函数.
当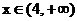 时,
时,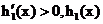 为增函数.
为增函数.
当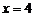 时
时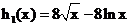 最小,
最小,
最小为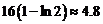 而
而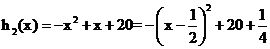 的
的
图象开口向下的抛物线.当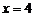 时,
时,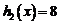
∴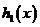 与
与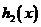 的大致图象如图:
的大致图象如图:
∴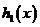 与
与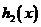 的交点个数为2个,即
的交点个数为2个,即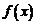 和
和 的图象的交点个数为2个.
的图象的交点个数为2个.
评注:本题中的(3)研究两条曲线的交点,解方程(组)比较麻烦,需要转为函数,利用函数的单调性进一步判断出交点的个数.
7.函数与方程在数列中的应用
例11.(2008陕西卷,理22)已知数列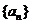 的首项
的首项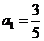 ,
,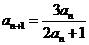 ,
,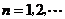 .
.
(Ⅰ)求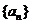 的通项公式;
的通项公式;
(Ⅱ)证明:对任意的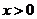 ,
,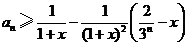 ,
,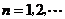 ;
;
(Ⅲ)证明: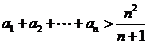 .
.
分析:(1)由递推关系求通项,可以进行变形,构造一个特殊数列求出;(2)不等式的左边只含有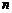 ,右边含有
,右边含有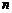 和
和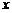 ,可以看作是关于
,可以看作是关于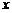 的函数,可证此函数的最大值
的函数,可证此函数的最大值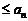 。
。
解法一:(Ⅰ)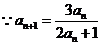 ,
,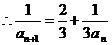 ,
,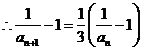 ,
,
又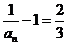 ,
, 是以
是以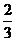 为首项,
为首项,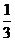 为公比的等比数列.
为公比的等比数列.
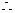
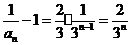 ,
, .
.
(Ⅱ)由(Ⅰ)知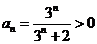 ,
,
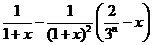
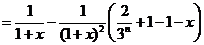
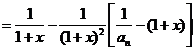
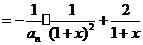
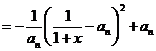
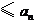 ,
,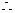 原不等式成立.
原不等式成立.
(Ⅲ)由(Ⅱ)知,对任意的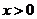 ,有
,有
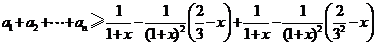
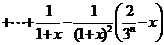
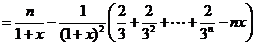 .
.
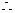 取
取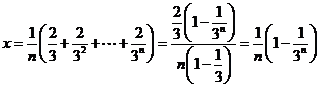 ,
,
则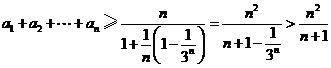 .
.
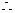 原不等式成立.
原不等式成立.
解法二:(Ⅰ)同解法一.
(Ⅱ)设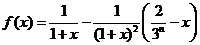 ,
,
则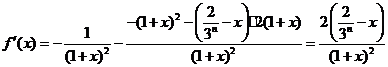
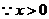 ,
,
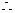 当
当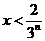 时,
时,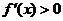 ;当
;当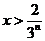 时,
时, ,
,
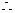 当
当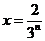 时,
时,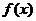 取得最大值
取得最大值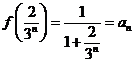 .
.
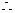 原不等式成立.
原不等式成立.
(Ⅲ)同解法一.
评注:本题为利用函数与方程的思想解答数列问题,在求右边函数的最值时,可以用配方法,也可以用导函数求得函数的单调性求其最值。
6、函数与方程在导数中的应用
例9.(2008湖南卷,理21)已知函数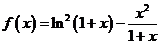 .
.
(I) 求函数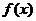 的单调区间;
的单调区间;
(Ⅱ)若不等式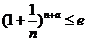 对任意的
对任意的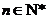 都成立(其中e是自然对数的底数).
都成立(其中e是自然对数的底数).
求 的最大值.
的最大值.
分析:由导数研究函数的单调性,求得函数的单调区间,不等式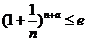 对任意的
对任意的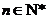 都成立可等价转化为不等式
都成立可等价转化为不等式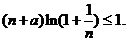 进而分离出
进而分离出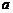 来,不等式恒成立转为函数研究最值问题,可构造函数利用导数研究函数的单调性,从而求出最值。
来,不等式恒成立转为函数研究最值问题,可构造函数利用导数研究函数的单调性,从而求出最值。
解: (Ⅰ)函数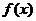 的定义域是
的定义域是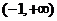 ,
,
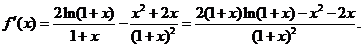
设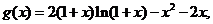 则
则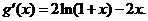
令 则
则
当 时,
时, 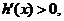
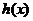 在(-1,0)上为增函数,
在(-1,0)上为增函数,
当x>0时,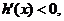
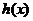 在
在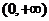 上为减函数.
上为减函数.
所以h(x)在x=0处取得极大值,而h(0)=0,所以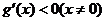 ,
,
函数g(x)在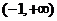 上为减函数.
上为减函数.
于是当 时,
时,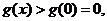
当x>0时,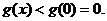
所以,当 时,
时,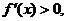
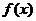 在(-1,0)上为增函数.
在(-1,0)上为增函数.
当x>0时,
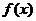 在
在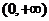 上为减函数.
上为减函数.
故函数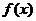 的单调递增区间为(-1,0),单调递减区间为
的单调递增区间为(-1,0),单调递减区间为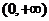 .
.
(Ⅱ)不等式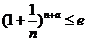 等价于不等式
等价于不等式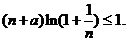 由
由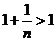 知,
知,
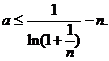 设
设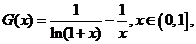 则
则
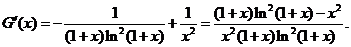
由(Ⅰ)知,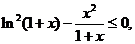 即
即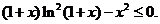
所以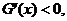
 于是G(x)在
于是G(x)在 上为减函数.
上为减函数.
故函数G(x)在 上的最小值为
上的最小值为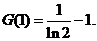
所以a的最大值为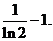
评注:第(1)问是为第二问铺垫的,在解答问题(2)时,不等式恒成立问题转化为函数研究最值,利用导数研究单调性,进而研究最值是解决函数最值问题的常用方法。理科的题目常常是超越方程或不等式,要利用导数解答问题。而文科的题基本上是含有参数的三次函数,如下一例题
例10.(2008北京卷,文17)已知函数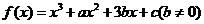 ,且
,且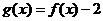 是奇函数.(Ⅰ)求
是奇函数.(Ⅰ)求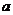 ,
, 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数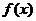 的单调区间.
的单调区间.
分析:本题从函数的性质入手,利用奇函数的定义,确定函数的解析式,,再由导数研究函数的单调性。
解:(Ⅰ)因为函数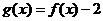 为奇函数,
为奇函数,
所以,对任意的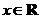 ,
,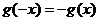 ,即
,即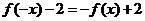 .
.
又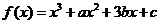
所以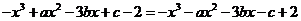 .
.
所以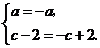
解得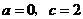 .
.
(Ⅱ)由(Ⅰ)得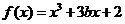 .
.
所以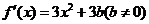 .
.
当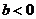 时,由
时,由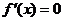 得
得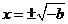 .
.
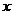 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
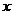 |
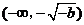 |
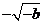 |
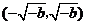 |
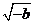 |
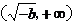 |
 |
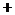 |
0 |
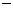 |
0 |
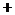 |
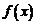 |
单调递增 |
极大值 |
单调递减 |
极小值 |
单调递增 |
所以,当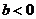 时,函数
时,函数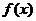 在
在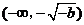 上单调递增,在
上单调递增,在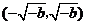 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
当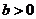 时,
时,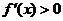 ,所以函数
,所以函数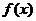 在
在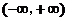 上单调递增.
上单调递增.
评注: 为奇函数是对任意的
为奇函数是对任意的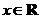 ,
,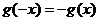 都成立来说的,也就是恒等式,对应项的系数相等,从而确定系数。在研究含有参数的函数的单调性时往往要对参数在分界值处进行分类讨论。
都成立来说的,也就是恒等式,对应项的系数相等,从而确定系数。在研究含有参数的函数的单调性时往往要对参数在分界值处进行分类讨论。
5、函数与方程在解析几何中的应用
例6.(2008山东淄博)若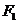 、
、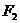 分别是椭圆
分别是椭圆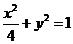 的左、右焦点.
的左、右焦点.
(Ⅰ)若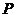 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求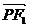
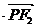 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点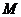
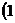 ,
,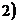 的直线
的直线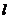 与椭圆交于两不同的点
与椭圆交于两不同的点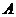 、
、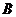 ,且
,且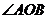 为锐角(其中
为锐角(其中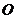 为坐标原点),求直线
为坐标原点),求直线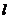 的斜率
的斜率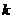 的取值范围.
的取值范围.
分析:(Ⅰ)中可以设出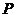 点的坐标,用坐标表示出
点的坐标,用坐标表示出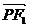
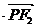 ,得到函数求最值。(Ⅱ)中研究直线与椭圆的交点,需要解方程组,由韦达定理解答即可。
,得到函数求最值。(Ⅱ)中研究直线与椭圆的交点,需要解方程组,由韦达定理解答即可。
解:(Ⅰ)解法一:由椭圆方程知
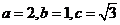
所以 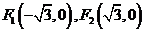 ,设
,设
则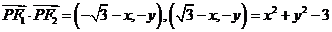
又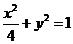 ∴
∴ 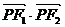
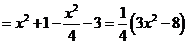
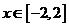 ,故当
,故当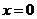 ,即点
,即点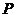 为椭圆短轴端点时,
为椭圆短轴端点时,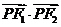 有最小值
有最小值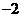
当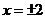 ,即点
,即点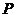 为椭圆长轴端点时,
为椭圆长轴端点时,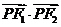 有最大值
有最大值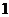 .
.
解法二:易知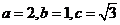 ,所以
,所以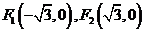 ,设
,设
则
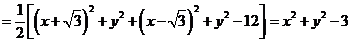
(以下同解法一)
(Ⅱ)显然当直线的斜率不存在即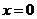 时,不满足题设条件
时,不满足题设条件
可设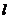 的方程为
的方程为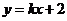 ,设
,设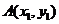 ,
,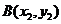
联立 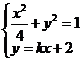 得
得
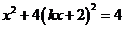
即 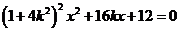
∴ 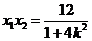 ,
,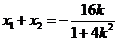
由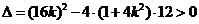
即 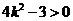 解得
解得
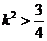 ①
①
又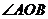 为锐角
为锐角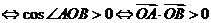
∴ 
∴ 
∴ 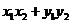
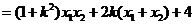
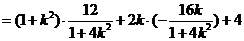
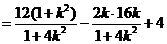

∴ 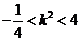 ②
②
综①、②可知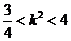
∴ 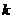 的取值范围是
的取值范围是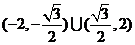 .
.
评注:解析几何中点的坐标,线的方程都与函数、方程是相通的,可以利用函数与方程的思想解答问题。在解方程组时要注意保证方程组有两不同的解,求得参数的取值范围。
例7.(2008广东卷,理18)设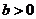 ,椭圆方程为
,椭圆方程为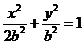 ,抛物线方程为
,抛物线方程为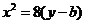 .如图4所示,过点
.如图4所示,过点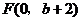 作
作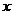 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为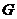 ,已知抛物线在点
,已知抛物线在点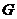 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点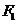 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点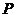 ,使得
,使得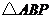 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
分析:本题中的抛物线可以看作为二次函数,抛物线在点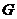 的切线的斜率就是该点处的函数的导数,由此可以写出此切线方程,从而得到椭圆的右焦点
的切线的斜率就是该点处的函数的导数,由此可以写出此切线方程,从而得到椭圆的右焦点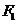 的坐标,进而求出椭圆和抛物线的方程,(2)为探索结论问题,
的坐标,进而求出椭圆和抛物线的方程,(2)为探索结论问题,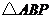 为直角三角形自然要考虑谁是直角,所以需要分类讨论,并转为方程确定其解的个数。
为直角三角形自然要考虑谁是直角,所以需要分类讨论,并转为方程确定其解的个数。
解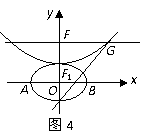 :(1)由
:(1)由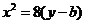 得
得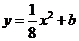 ,当
,当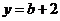 得
得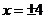 ,
,
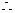 G点的坐标为
G点的坐标为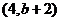 ,
,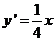 ,
,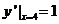 ,
,
过点G的切线方程为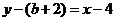 即
即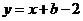 ,
,
令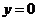 得
得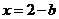 ,
,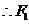 点的坐标为
点的坐标为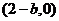 ,由椭圆方程得
,由椭圆方程得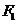 点的坐标为
点的坐标为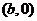 ,
,
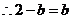 即
即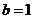 ,即椭圆和抛物线的方程分别为
,即椭圆和抛物线的方程分别为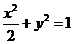 和
和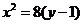 ;
;
(2)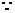 过
过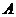 作
作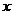 轴的垂线与抛物线只有一个交点
轴的垂线与抛物线只有一个交点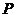 ,
, 以
以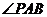 为直角的
为直角的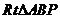 只有一个,同理
只有一个,同理 以
以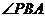 为直角的
为直角的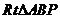 只有一个。若以
只有一个。若以 为直角,设
为直角,设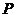 点坐标为
点坐标为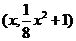 ,
,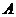 、
、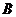 两点的坐标分别为
两点的坐标分别为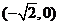 和
和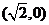 ,
,
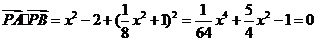 。关于
。关于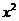 的二次方程有一大于零的解,
的二次方程有一大于零的解,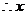 有两解,即以
有两解,即以 为直角的
为直角的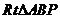 有两个,因此抛物线上存在四个点使得
有两个,因此抛物线上存在四个点使得 为直角三角形。
为直角三角形。
评注:本题较好地把圆锥曲线问题和函数的导函数结合起来解答问题,一般地,对于已经曲线的某一点处的切线,就要转为函数求导,从而求出其切线。另外,还要注意方程的解的个数的探讨。
例8.(2008湖南,理20)若A、B是抛物线y2=4x上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点P,则称弦AB是点P的一条“相关弦”。已知当x>2时,点P(x,0)存在无穷多条“相关弦”。给定x0>2.
(I)证明:点P(x0,0)的所有“相关弦”的中点的横坐标相同;
(II) 试问:点P(x0,0)的“相关弦”的弦长中是否存在最大值?
若存在,求其最大值(用x0表示):若不存在,请说明理由.
分析:本题(1)研究中点弦问题,可以用点差法,求得中点的坐标从而证明;(2)可用中点的坐标表示出弦长,得到关于中点的纵坐标的函数,再求出函数的值域。
解: (I)设AB为点P(x0,0)的任意一条“相关弦”,且点A、B的坐标分别是
(x1,y1)、(x2,y2)(x1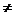 x2),则y21=4x1, y22=4x2,
x2),则y21=4x1, y22=4x2,
两式相减得(y1+y2)(y1-y2)=4(x1-x2).因为x1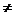 x2,所以y1+y2
x2,所以y1+y2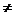 0.
0.
设直线AB的斜率是k,弦AB的中点是M(xm, ym),则
k=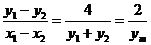 .从而AB的垂直平分线l的方程为
.从而AB的垂直平分线l的方程为 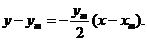
又点P(x0,0)在直线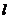 上,所以
上,所以 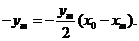
而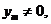 于是
于是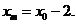 故点P(x0,0)的所有“相关弦”的中点的横坐标都是x0-2.
故点P(x0,0)的所有“相关弦”的中点的横坐标都是x0-2.
(Ⅱ)由(Ⅰ)知,弦AB所在直线的方程是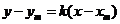 ,代入
,代入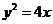 中,
中,
整理得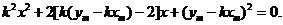 (·)
(·)
则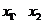 是方程(·)的两个实根,且
是方程(·)的两个实根,且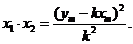
设点P的“相关弦”AB的弦长为l,则
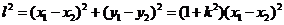
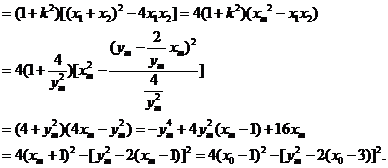
因为0<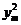 <4xm=4(xm-2)
=4x0-8,于是设t=
<4xm=4(xm-2)
=4x0-8,于是设t=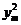 ,则t
,则t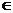 (0,4x0-8).
(0,4x0-8).
记l2=g(t)=-[t-2(x0-3)]2+4(x0-1)2.
若x0>3,则2(x0-3) 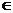 (0,
4x0-8),所以当t=2(x0-3),即
(0,
4x0-8),所以当t=2(x0-3),即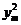 =2(x0-3)时,
=2(x0-3)时,
l有最大值2(x0-1).
若2<x0<3,则2(x0-3)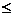 0,g(t)在区间(0,4 x0-8)上是减函数,
0,g(t)在区间(0,4 x0-8)上是减函数,
所以0<l2<16(x0-2),l不存在最大值.
综上所述,当x0>3时,点P(x0,0)的“相关弦”的弦长中存在最大值,且最大值
为2(x0-1);当2< x0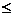 3时,点P(x0,0)的“相关弦”的弦长中不存在最大值.
3时,点P(x0,0)的“相关弦”的弦长中不存在最大值.
评注:本题中需要解方程组求弦长,弦长用弦的中点坐标表示出来,可用配方法求得函数的值域。直线与圆锥曲线的位置关系中渗透着函数与方程的思想,在解决解析几何问题时常常运用函数与方程的思想来解答。
4、函数与方程在立体几何中的应用
例5.(2008北京卷,理,8)如图,动点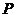 在正方体
在正方体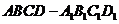 的对角线
的对角线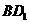 上.过点
上.过点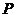 作垂直于平面
作垂直于平面 的直线,与正方体表面相交于
的直线,与正方体表面相交于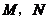 .设
.设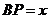 ,
,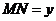 ,
,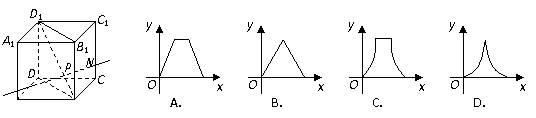 则函数
则函数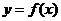 的图象大致是( )
的图象大致是( )

分析:本题是立体几何与函数的交汇题,可以先观察题目并进行空间想象加以判断,再由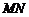 的特殊性与平面
的特殊性与平面 垂直,可以把
垂直,可以把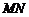 向平面
向平面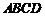 内作正投影,保持其长度不变,从而把空间问题转为平面问题,在平面内研究函数关系即可顺利完成。
内作正投影,保持其长度不变,从而把空间问题转为平面问题,在平面内研究函数关系即可顺利完成。
 解:设正方体的棱长为
解:设正方体的棱长为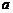 ,由图形的对称性知
,由图形的对称性知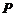 点始终是
点始终是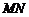 的中点,
的中点,
而且随着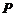 点从
点从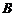 点向
点向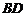 的中点滑动,
的中点滑动,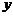 值逐渐增大到最大,再由中
值逐渐增大到最大,再由中
点向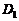 点滑动,而逐渐变小,排除
点滑动,而逐渐变小,排除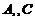 ,把
,把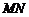 向平面
向平面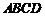 内正投
内正投
影得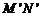 ,则
,则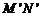 =
=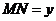 ,由于
,由于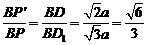 ,
,
∴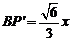 ,所以当
,所以当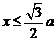 时,
时,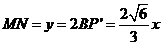 为一次函数,故选
为一次函数,故选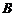
答案: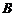
评注:本题为函数的变化趋势问题,通过观察进行理性地分析,再从数值上加以运算。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com