
10. 椭圆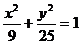 上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
上的一点P到两焦点的距离的乘积为m,则当m取最大值时,点P的坐标是_____________________.
讲解
记椭圆的二焦点为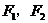 ,有
,有
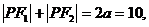
则知
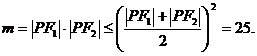
显然当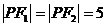 ,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
,即点P位于椭圆的短轴的顶点处时,m取得最大值25.
故应填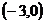 或
或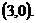
9.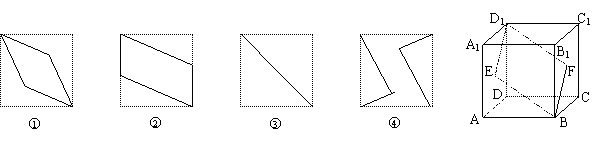 如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
如右图,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 .(要求:把可能的图的序号都填上)
讲解 因为正方体是对称的几何体,所以四边形BFD1E在该正方体的面上的射影可分为:上下、左右、前后三个方向的射影,也就是在面ABCD、面ABB1A1、面ADD1A1上的射影.
四边形BFD1E在面ABCD和面ABB1A1上的射影相同,如图2所示;
四边形BFD1E在该正方体对角面的ABC1D1内,它在面ADD1A1上的射影显然是一条线段,如图3所示. 故应填23.
8. 过长方体一个顶点的三条棱长为3、4、5, 且它的八个顶点都在同一球面上,这个球的表面积是________.
讲解 长方体的对角线就是外接球的直径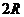 , 即有
, 即有
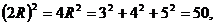
从而 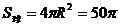 ,故应填
,故应填
7. 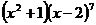 的展开式中
的展开式中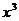 的系数是
的系数是
讲解 由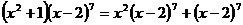 知,所求系数应为
知,所求系数应为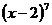 的x项的系数与
的x项的系数与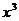 项的系数的和,即有
项的系数的和,即有
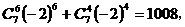
故应填1008.
6.某商场开展促销活动,设计一种对奖券,号码从000000到999999. 若号码的奇位数字是不同的奇数,偶位数字均为偶数时,为中奖号码,则中奖面(即中奖号码占全部号码的百分比)为 .
讲解 中奖号码的排列方法是: 奇位数字上排不同的奇数有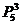 种方法,偶位数字上排偶数的方法有
种方法,偶位数字上排偶数的方法有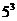 ,从而中奖号码共有
,从而中奖号码共有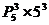 种,于是中奖面为
种,于是中奖面为
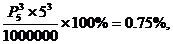
故应填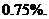
5.以下四个命题:
①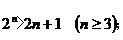
②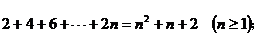
③凸n边形内角和为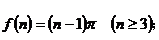 ④凸n边形对角线的条数是
④凸n边形对角线的条数是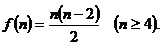
其中满足“假设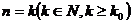 时命题成立,则当n=k+1时命题也成立’’.但不满足“当
时命题成立,则当n=k+1时命题也成立’’.但不满足“当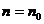 (
(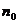 是题中给定的n的初始值)时命题成立”的命题序号是 .
是题中给定的n的初始值)时命题成立”的命题序号是 .
讲解 ①当n=3时,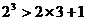 ,不等式成立;
,不等式成立;
②
当n=1时,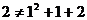 ,但假设n=k时等式成立,则
,但假设n=k时等式成立,则
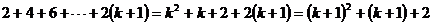 ;
;
③ 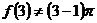 ,但假设
,但假设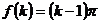 成立,则
成立,则
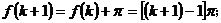
④ 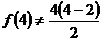 ,假设
,假设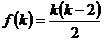 成立,则
成立,则
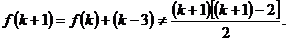
故应填②③.
4. 如果函数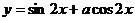 的图象关于直线
的图象关于直线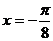 对称,那么
对称,那么
讲解 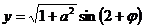 ,其中
,其中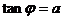 .
.
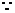
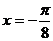 是已知函数的对称轴,
是已知函数的对称轴,
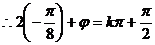 ,
,
即 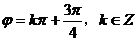 ,
,
于是 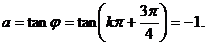 故应填
故应填
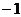 .
.
3.如果函数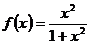 ,那么
,那么 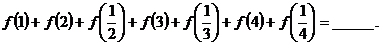
讲解 容易发现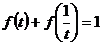 ,这就是我们找出的有用的规律,于是
,这就是我们找出的有用的规律,于是
原式=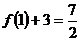 ,应填
,应填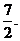
当全部情况为有限种时,也可采用淘汰法。
例18. 已知,则与同时成立的充要条件是____________。
解:按实数b的正、负分类讨论。
当b>0时,而等式不可能同时成立;
当b=0时,无意义;
当b<0时,若a<0,则两不等式不可能同时成立,以上三种情况均被淘汰,故只能为a>0,b<0,容易验证,这确是所要求的充要条件。
跟踪训练:
1已知函数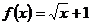 ,则
,则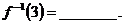
讲解 由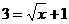 ,得
,得
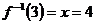 ,应填4.
,应填4.
2. 集合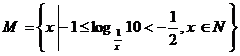 的真子集的个数是
的真子集的个数是
讲解 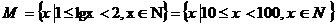 ,显然集合M中有90个元素,其真子集的个数是
,显然集合M中有90个元素,其真子集的个数是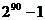 ,应填
,应填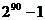 .
.
通过“化复杂为简单、化陌生为熟悉”,将问题等价地转化成便于解决的问题,从而得出正确的结果。
例14(08湖南理)设函数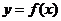 存在反函数
存在反函数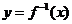 ,且函数
,且函数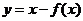 的图象过点(1,2),
的图象过点(1,2),
则函数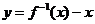 的图象一定过点 .
的图象一定过点 .
解:由函数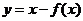 的图象过点(1,2)得:
的图象过点(1,2)得: 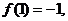 即函数
即函数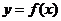 过点
过点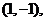 则其反函数过点
则其反函数过点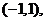 所以函数
所以函数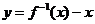 的图象一定过点
的图象一定过点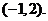
例15 不等式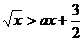 的解集为(4,b),则a=
,b=
。
的解集为(4,b),则a=
,b=
。
解:设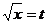 ,则原不等式可转化为:
,则原不等式可转化为: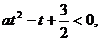 ∴a > 0,且2与
∴a > 0,且2与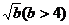 是方程
是方程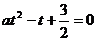 的两根,由此可得:
的两根,由此可得: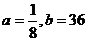 。
。
例16 不论k为何实数,直线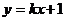 与曲线
与曲线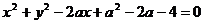 恒有交点,则实数a的取值范围是 。
恒有交点,则实数a的取值范围是 。
解:题设条件等价于点(0,1)在圆内或圆上,或等价于点(0,1)到圆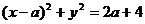 ,
,
∴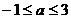 。
。
例17 函数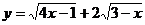 单调递减区间为
。
单调递减区间为
。
解:易知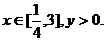 ∵y与y2有相同的单调区间,而
∵y与y2有相同的单调区间,而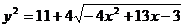 ,∴可得结果为
,∴可得结果为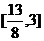 。
。
总之,能够多角度思考问题,灵活选择方法,是快速准确地解数学填空题的关键。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com