
6. (2009山东文)已知定义在R上的奇函数 ,满足
,满足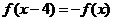 ,且在区间[0,2]上是增函数,则 ( D
).
,且在区间[0,2]上是增函数,则 ( D
).
A. B.
B. 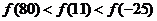
C. 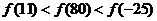 D.
D.
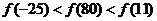
二 填空题
5.(2009浙江文)若函数 ,则下列结论正确的是(
C )
,则下列结论正确的是(
C )
A.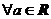 ,
, 在
在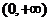 上是增函数21世纪教育网
上是增函数21世纪教育网
B.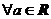 ,
, 在
在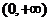 上是减函数
上是减函数
C. ,
, 是偶函数
是偶函数
D. ,
, 是奇函数
是奇函数
4. (2009广东文)函数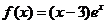 的单调递增区间是 ( D )
的单调递增区间是 ( D )
A. 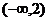 B. (0,3) C. (1,4) D.
B. (0,3) C. (1,4) D. 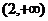 21世纪教育网
21世纪教育网
3.(2006年天津卷)已知函数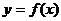 的图象与函数
的图象与函数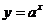 (
(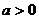 且
且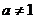 )的图象关于直线
)的图象关于直线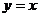 对称,记
对称,记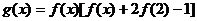 .若
.若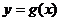 在区间
在区间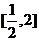 上是增函数,则实数
上是增函数,则实数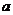 的取值范围是( D )
的取值范围是( D )
A.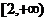 B.
B.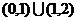 C.
C.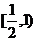 D.
D.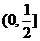
2.(2006陕西)已知函数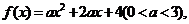 若
若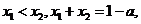 则( A )
则( A )
A.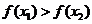 B.
B.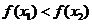
C.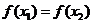 D.
D.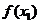 与
与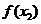 的大小不能确定
的大小不能确定
1.( 2006年湖南)“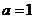 ”是“函数
”是“函数 在区间[1, +∞)上为增函数”的( A
)
在区间[1, +∞)上为增函数”的( A
)
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.
如果二次函数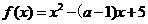 在区间
在区间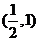 上是增函数,求
上是增函数,求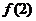 的取值范围.
的取值范围.
[解析]二次函数 在区间
在区间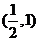 上是增函数,由于其图象(抛物线)开口向上,故其对称轴
上是增函数,由于其图象(抛物线)开口向上,故其对称轴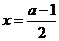 或与直线
或与直线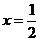 重合或位于直线
重合或位于直线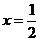 的左侧,于是
的左侧,于是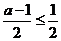 ,解之得
,解之得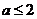 ,故
,故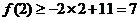 ,即
,即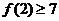 .
.
能力训练
2.(2004广东)设函数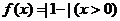 ,证明:当
,证明:当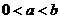 ,且
,且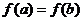 时,
时,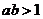 .
.
[证明] 在
在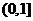 上是减函数,在
上是减函数,在 上是增函数.由
上是增函数.由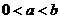 且
且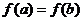 ,得
,得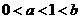 且
且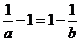 ,即
,即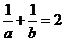

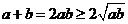 ,
,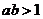 .
.
[题型3] 函数的值域或最值
[例3](2006江苏)设a为实数,记函数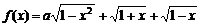 的最大值为
的最大值为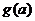 .
.
(1)设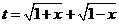 ,求t的取值范围,并把
,求t的取值范围,并把 表示为t的函数
表示为t的函数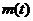 ;
;
(2)求g(a);
(3)试求满足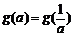 的所有实数a.
的所有实数a.
[解析](1)∵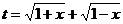 ,
,
∴要使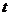 有意义,必须
有意义,必须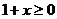 且
且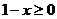 ,即
,即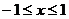 .
.
∵ ,且
,且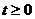 ……① ∴
……① ∴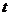 的取值范围是
的取值范围是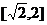 .
.
由①得: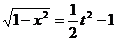 ,∴
,∴
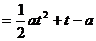 ,
,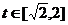 .
.
(2)由题意知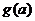 即为函数
即为函数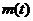
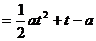 ,
,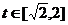 的最大值,
的最大值,
∵直线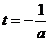 是抛物线
是抛物线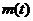
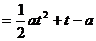 的对称轴,∴可分以下几种情况进行讨论:
的对称轴,∴可分以下几种情况进行讨论:
(1)当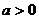 时,函数
时,函数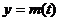 ,
,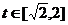 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由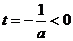 知
知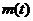 在
在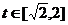 上单调递增,故
上单调递增,故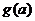
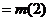
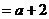 ;
;
(2)当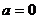 时,
时, ,
,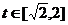 ,有
,有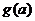 =2;
=2;
(3)当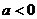 时,,函数
时,,函数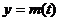 ,
,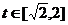 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若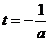
 即
即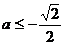 时,
时,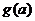
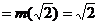 ,
,
若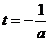
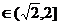 即
即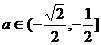 时,
时,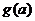
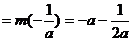 ,
,
若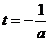
 即
即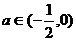 时,
时,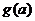
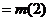
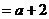 .
.
综上所述,有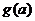 =
= .
.
(3)当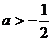 时,
时,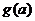
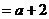
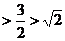 ;
;
当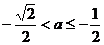 时,
时,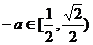 ,
,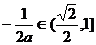 ,∴
,∴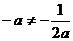 ,
,
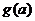
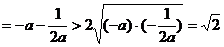 ,故当
,故当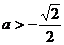 时,
时,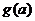
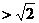 ;
;
当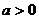 时,
时,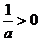 ,由
,由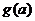
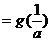 知:
知:
 ,故
,故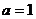 ;
;
当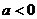 时,
时,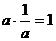 ,故
,故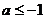 或
或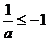 ,从而有
,从而有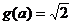 或
或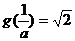 ,
,
要使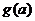
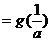 ,必须有
,必须有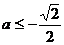 ,
,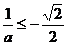 ,即
,即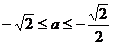 ,
,
此时,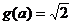
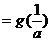 。
。
综上所述,满足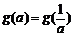 的所有实数a为:
的所有实数a为: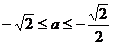 或
或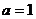 .
.
[点评]本题主要考查函数、方程等基本知识,考查分类讨论的数学思想方法和综合运用数学知识分析问题和解决问题的能力.
[变式与拓展]
1. 设函数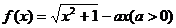 ,求证:当且仅当
,求证:当且仅当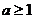 时,
时, 在
在 内为单调函数;
内为单调函数;
[解析]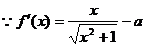 ,
,
①当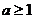 时,∵
时,∵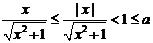 ,∴
,∴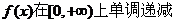 ,
,
②当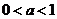 时,由
时,由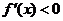 ,得
,得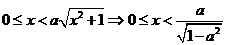 ;
;
由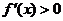 得
得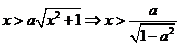 ;
;
∴当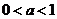 时,
时, 在
在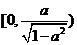 上为减函数,在
上为减函数,在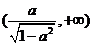 上为增函数,
上为增函数,
∴当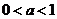 时,
时, 在
在
 上不是单调函数.
上不是单调函数.
综上,当且反当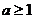 时,
时, 在
在 上为单调函数.
上为单调函数.
[题型2] 利用单调性讨论参数的范围
[例2]已知函数 )的图象与函数
)的图象与函数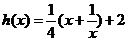 的图象关于点
的图象关于点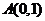 对称.
对称.
(1)求m的值;
(2)若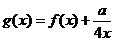 在区间
在区间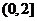 上为减函数,求实数a的取值范围.
上为减函数,求实数a的取值范围.
[解析](1)设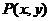 为函数
为函数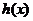 图象上一点,点
图象上一点,点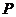 关于
关于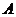 的对称点为
的对称点为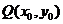 ,
,
则有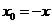 ,且
,且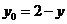 .
.
∵点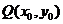 在
在 上,
上,
∴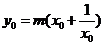 .
.
消去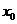 、
、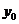 代入,得
代入,得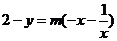 ,
,
整理,得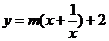 ,∴m=
,∴m= .
.
(2)∵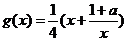 ,设
,设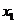 、
、 ,且
,且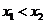 ,
,
则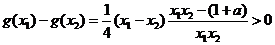 对一切x1、x2∈(0,2]恒成立.
对一切x1、x2∈(0,2]恒成立.
∴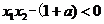 对一切
对一切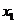 、
、 恒成立.
恒成立.
∴由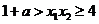 ,得
,得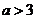 .
.
[变式与拓展]
4.函数的最值:函数的最值是是函数值域中的特殊值,故求函数最值的方法与求值域的方法差不多,要考虑取“=”的条件是否满足.
典例剖析
[题型1]函数单调性的判断与证明
[例1]定义在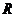 上的函数
上的函数 ,
, ,当
,当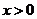 时,
时,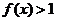 ,且对任意的
,且对任意的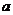 、
、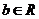 ,有
,有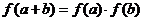 .
.
(1)求证: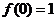 ;
(2)求证:对任意的
;
(2)求证:对任意的 ,恒有
,恒有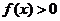 ;
;
(3)求证: 是
是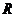 上的增函数;
(4)若
上的增函数;
(4)若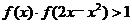 ,求x的取值范围.
,求x的取值范围.
[解析](1)证明:令 ,则
,则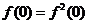 ,又
,又 ,∴
,∴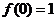 .
.
(2)证明:当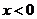 时,
时,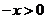 ,∴
,∴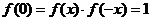 ,
,
∴f(-x)= ,又
,又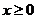 时,
时,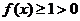 ,
,
∴ 时,恒有
时,恒有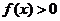 .
.
(3)证明:设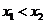 ,则
,则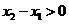 ,
,
∴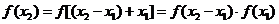 .
.
∵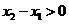 ,∴
,∴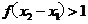 ,
,
又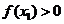 ,∴
,∴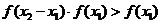 ,
,
∴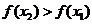 ,∴
,∴ 是
是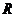 上的增函数.
上的增函数.
(4)解:由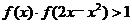 ,
,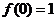 ,得
,得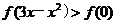 ,又
,又 是
是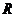 上的增函数,∴
上的增函数,∴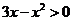 ,∴
,∴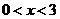 .
.
[点评]解本题的关键是灵活应用题目条件,尤其是(3)中“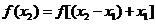 ”是证明单调性的关键,这里体现了向条件化归的策略.
”是证明单调性的关键,这里体现了向条件化归的策略.
[变式与拓展]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com