
8.若函数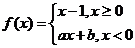 为偶函数,则
为偶函数,则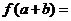
 .
.
7.(2007年宁夏)设函数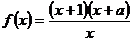 为奇函数,则实数
为奇函数,则实数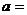
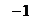 .
.
6. (2007年全国Ⅰ)设 ,
,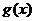 是定义在R上的函数,
是定义在R上的函数,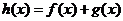 ,则“
,则“ ,
,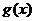 均为偶函数”是“
均为偶函数”是“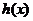 为偶函数”的( B )
为偶函数”的( B )
A.充要条件 B.充分而不必要的条件
C.必要而不充分的条件 D.既不充分也不必要的条件
5.(2008年福建)函数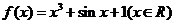 ,若
,若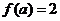 ,则
,则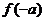 的值为( B )
的值为( B )
A.3 B. 0 C. -1 D.-2
4. 定义在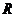 上的奇函数
上的奇函数 的最小正周期为3,则下列关系中恒成立的是( B )
的最小正周期为3,则下列关系中恒成立的是( B )
A.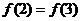 B.
B.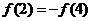
C.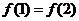 D.
D. 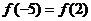
3. (2008全国Ⅱ)函数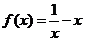 的图像关于( C )
的图像关于( C )
A.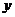 轴对称 B.
直线
轴对称 B.
直线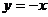 对称
对称
C. 坐标原点对称
D. 直线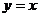 对称
对称
2.下列函数中为奇函数的是 ( C )
A. 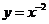 B.
B. 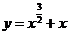
C. 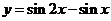 D.
D. 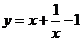
1.二次函数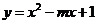 是偶函数,则函数的增区间为 ( A )
是偶函数,则函数的增区间为 ( A )
A.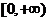 B.
B.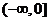 C.
C.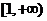 D.
D.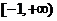
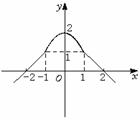
2.设 为定义在
为定义在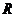 上的偶函数,当
上的偶函数,当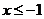 时,
时,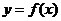 的图象是经过点
的图象是经过点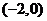 ,斜率为
,斜率为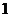 的射线,又在
的射线,又在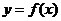 的图象中有一部分是顶点在
的图象中有一部分是顶点在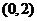 ,且过点
,且过点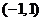 的一段抛物线
的一段抛物线 .试写出函数
.试写出函数 的表达式,并作出其图象.
的表达式,并作出其图象.
[解析]当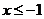 时,设
时,设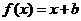 ,则由
,则由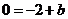 ,即
,即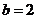 ,得
,得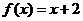 ;
;
 当
当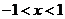 时,设
时,设 ,
,
则由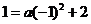 ,即
,即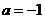 ,得
,得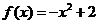 ;
;
当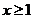 时,
时,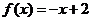 .
.
故f(x)= .
.
[题型3] 函数的周期问题
[例3] 求下列函数的周期:
(1)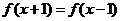 (2)
(2)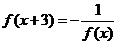
[解析](1)由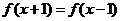 得,
得,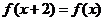 ,所以函数周期为
,所以函数周期为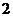
(2)由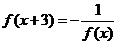 得,
得,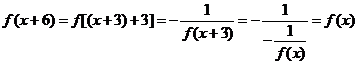 ,所以函数的周期为
,所以函数的周期为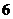 .
.
[点评]这是一个抽象函数的周期问题,注意已知等式中变量的替换,再与周期的定义结合,就可以得出周期.
[变式与拓展]
已知偶函数 是定义在
是定义在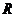 上的周期函数,其最小正周期为4.
上的周期函数,其最小正周期为4.
(1)若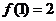 ,求
,求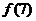 的值;
的值;
(2)若 在
在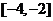 上递增,则下列关系中正确的是( )
上递增,则下列关系中正确的是( )
A.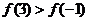 B.
B. 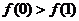
C.  D.
D. 
[解析](1)∵4是函数的周期,∴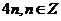 也是函数的周期.
也是函数的周期.
于是,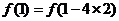
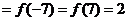 .
.
(2)偶函数在在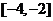 上递增,则在[2,4]上递减。由函数的最小正周期为4知,
上递增,则在[2,4]上递减。由函数的最小正周期为4知, 在[0,2]上递增。排除(B),又
在[0,2]上递增。排除(B),又 ,排除(D).
,排除(D).
∵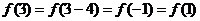 ,∴选(C).
,∴选(C).
能力训练
1.判断下列函数的奇偶性
(1)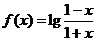
(2)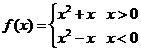
[解析](1)由 ,得
,得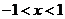 ,定义域关于原点对称,
,定义域关于原点对称,
又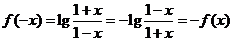 ,所以
,所以 是定义域上的奇函数.
是定义域上的奇函数.
(2)定义域为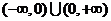 ,关于原点对称,
,关于原点对称,
又当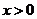 时,
时,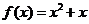 ,则
,则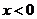 时,
时,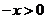 ,
,
∴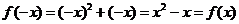 ,
,
又当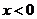 时,
时,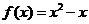 ,则
,则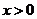 时,
时,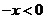 ,
,
∴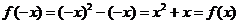 ,
,
故原函数为偶函数.
[题型2]函数奇偶性的应用
[例2]设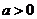 ,
,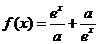 是R上的偶函数.
是R上的偶函数.
(1)求a的值;
(2)证明 在
在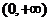 上是增函数.
上是增函数.
[解析](1)∵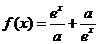 是
是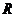 上的偶函数,∴
上的偶函数,∴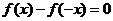 .
.
∴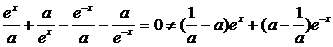
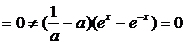
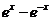 不可能恒为“
不可能恒为“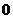 ”,∴当
”,∴当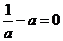 时等式恒成立,∴a=1.
时等式恒成立,∴a=1.
(2)在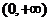 上任取
上任取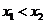 ,
,
f(x1)-f(x2)=
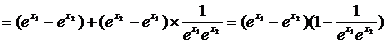
∵e>1,∴0<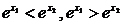 >1,∴
>1,∴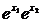 >1
>1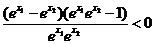 ,
,
∴ ,∴
,∴ 是在
是在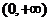 上的增函数.
上的增函数.
[点评]本题主要考查了函数的奇偶性以及单调性的基础知识.
[变式与拓展]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com