
1. (2006福建卷)已知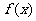 是周期为2的奇函数,当
是周期为2的奇函数,当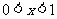 时,
时,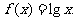 设
设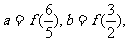
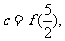 则( )
则( )
(A)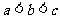 (B)
(B)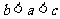 (C)
(C)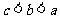 (D)
(D)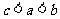
5.
设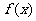 是R上的任意函数,则下列叙述正确的是
A)
是R上的任意函数,则下列叙述正确的是
A)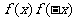 是奇函数 B)
是奇函数 B)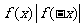 是奇函数
C)
是奇函数
C) 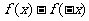 是偶函数 (D)
是偶函数 (D)  是偶函数
是偶函数
[例题讲解]
例1:判断下列函数的奇偶性(先看定义域,后看f(x)与f(-x)关系)
1)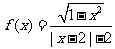 2)
2)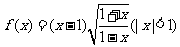
3)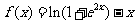
例2:设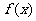 是
是 上的奇函数,
上的奇函数,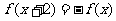 ,当
,当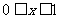 时,
时,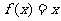 ,则
,则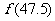 等于_______
等于_______
[变题]设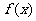 是定义在实数集R上的函数,且满足
是定义在实数集R上的函数,且满足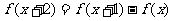 ,如果
,如果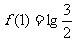 ,
,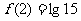 ,求
,求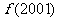
例3:设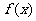 是定义在
是定义在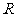 上的奇函数,且
上的奇函数,且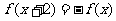 ,又当
,又当 时,
时,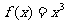 ,(1)证明:直线
,(1)证明:直线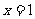 是函数
是函数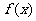 图象的一条对称轴:(2)当
图象的一条对称轴:(2)当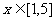 时,求
时,求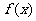 的解析式。
的解析式。
[变题]设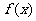 是定义在
是定义在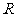 上的奇函数,且它的图象关于直线
上的奇函数,且它的图象关于直线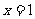 对称,求证:
对称,求证: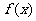 是周期函数.
是周期函数.
[命题展望]
4.
若函数f(x)是定义在R上的偶函数,在 上是减函数,且f(2)=0,则使得f(x)<0的x的取值范围是_______
上是减函数,且f(2)=0,则使得f(x)<0的x的取值范围是_______
3.
若函数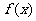 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当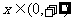 时,
时,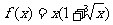 ,那么当x∈(-∞,0)时,f(x) =_______
,那么当x∈(-∞,0)时,f(x) =_______
2.
若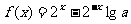 为奇函数,则实数
为奇函数,则实数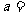 _______;
_______;
1. 如果定义在区间 上的函数
上的函数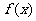 为奇函数,则
为奇函数,则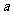 =______;
=______;
3、 注意点: 判断函数奇偶时,应先看定义域是否关于原点对称,后看f(x)与f(-x)关系
[课前预习]
2、
有关结论:
①若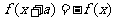 ,则
,则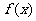 是__②若
是__②若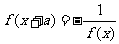 ,则
,则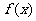 是__
③若
是__
③若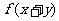 =
=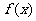 +
+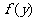 ,则
,则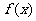 是____
④奇函数的图象关于______对称,偶函数的图象关于______对称
⑤若f(x)是定义在R上的奇函数,则有f(0)=_______;(★)
⑥若函数
是____
④奇函数的图象关于______对称,偶函数的图象关于______对称
⑤若f(x)是定义在R上的奇函数,则有f(0)=_______;(★)
⑥若函数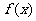 有两条对称轴x=a,x=b,则
有两条对称轴x=a,x=b,则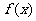 是周期函数,其周期为___
是周期函数,其周期为___
1、 相关概念: 1)对于函数f(x)中定义域中的任意x,恒有____,则f(x)为奇函数; 对于函数f(x)中定义域中的任意x,恒有____,则f(x)为偶函数;
2)若存在一个非零常数T,使函数f(x)中定义域中的任意x,恒有___,则f(x)是周期函数,T是它的一个周期;
2. 能运用函数的奇偶性与周期性解决有关函数问题;
[基本知识]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com