
14. 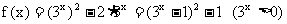
令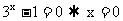 , 所以当
, 所以当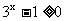 或
或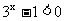 时存在反函数,
时存在反函数,
即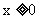 或
或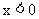 时(或它的子集)存在反函数,
时(或它的子集)存在反函数,
①当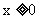 时, 即
时, 即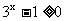

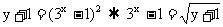
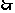
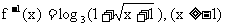
②当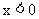 时, 即
时, 即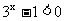


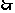
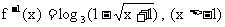
13. (1)
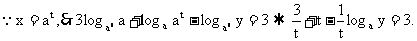
 .
.
(2) 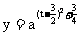
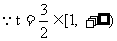
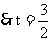 时,
时, 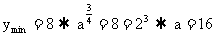
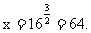
12. (1)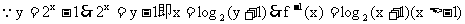
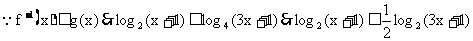
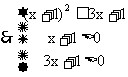
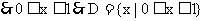
(2) 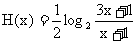
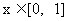 ,
, 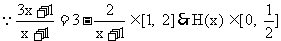
11. 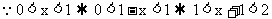 ,
,
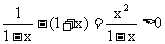 ,
, 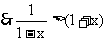
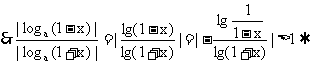 |
|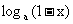 |
|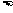 |
|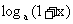 |.
|.
7. 110 ; 8.  9.
9. 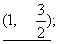 10.
10. 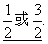
(二) 专题测试与练习
(一) 典型例题
例1 (1) 因为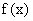 在R上是奇函数, 所以
在R上是奇函数, 所以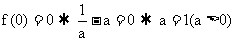 ,
,
(2) 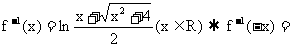
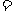
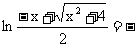
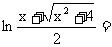
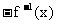 ,
, 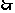
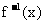 为奇函数.
为奇函数.
用定义法可证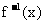 为单调增函数.
为单调增函数.
(也可用原函数证明)
例2 设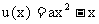 , 对称轴
, 对称轴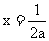 .
.
(1) 当 时,
时, 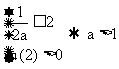 ;
;
(2) 当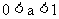 时,
时, 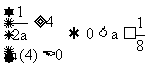 . 综上所述:
. 综上所述:

例3 由

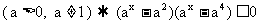
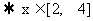
由y=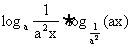
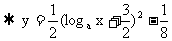
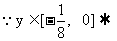
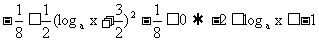 ,
, 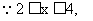
①
当 时, 为
时, 为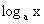 单调增函数,
单调增函数, 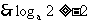 且
且
②
当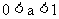 时, 为
时, 为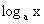 单调减函数,
单调减函数, 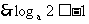 且
且
11. 设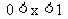 , 试比较|
, 试比较|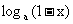 |与|
|与|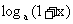 |的大小.
|的大小.
12. 已知函数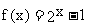 的反函数为
的反函数为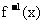 ,
, 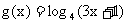 .
.
(1) 若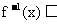
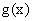 ,求
,求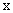 的取值范围D;
的取值范围D;
(2) 设函数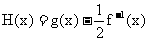 ,当
,当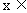 D时, 求函数
D时, 求函数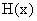 的值域.
的值域.
13. 已知常数 , 变数x、y有关系
, 变数x、y有关系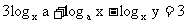 .
.
(1)若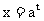
 , 试以a、t表示y ;
, 试以a、t表示y ;
(2)若t在 内变化时, y有最小值8, 求此时a和x的值各为多少?
内变化时, y有最小值8, 求此时a和x的值各为多少?
14. 已知函数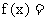
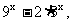 判断f (x)是否有反函数? 若有, 求出反函数; 若没有, 怎么改变
判断f (x)是否有反函数? 若有, 求出反函数; 若没有, 怎么改变
定义域后就有反函数了?
指数函数和对数函数解答
10.函数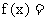
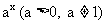 在
在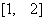 上的最大值比最小值大
上的最大值比最小值大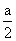 , 则a的值为
.
, 则a的值为
.
9. 已知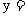
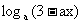 在
在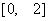 上是x的减函数, 则a的取值范围是
.
上是x的减函数, 则a的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com