
16、(12分)已知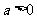 ,设命题
,设命题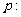 函数
函数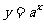 在
在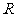 上单调递增,命题
上单调递增,命题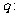 不等式
不等式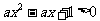 对
对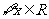 恒成立。若“
恒成立。若“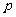 且
且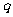 ”为假,“
”为假,“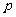 或
或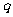 ”为真,求
”为真,求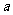 的取值范围。
的取值范围。
解:由函数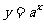 在
在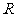 上单调递增,可得
上单调递增,可得 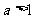
再由不等式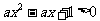 对
对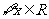 恒成立,可得
恒成立,可得
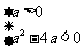
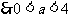
由于“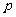 且
且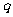 ”为假,“
”为假,“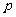 或
或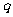 ”为真,故有
”为真,故有
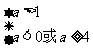 或
或 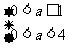

15、(12分)已知集合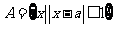 ,
,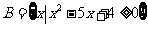 ,若
,若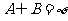 ,求实
,求实
数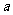 的取值范围。
的取值范围。
解:
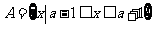 ,
,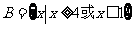
又
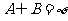 ,故有
,故有
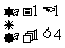
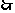
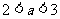
14、 3
11、 c>b>a 12、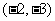 13、
13、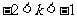 或
或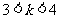
14、某工程由A,B,C,D四道工序组成,完成它们需用时间依次为2,5,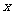 ,4天。四
,4天。四
道工序的先后顺序及相互关系是:A,B可以同时开工;A完成后,C可以开工;B,C完
成后,D可以开工。若该工程总时数为9天,则完成工序C需要的天数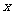 最大是
最大是
2010~2011年度汕头市金山中学
高三第一学期期中考数学(文)试卷
班级 姓名 座号 评分
13、已知方程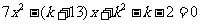 有2个不等实根
有2个不等实根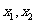 ,且
,且
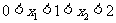 ,则实数
,则实数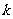 的取值范围是
的取值范围是
12、函数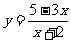 的图象关于点
对称
的图象关于点
对称
11、已知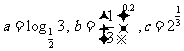 ,则
,则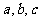 的大小关系是
的大小关系是
10、已知非负函数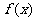 在
在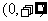 上满足
上满足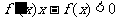 ,且
,且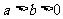 则
则
A、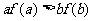 B、
B、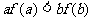 C、
C、 D、
D、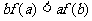
9. 已知 ,则函数
,则函数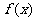 的最小值是
的最小值是
A. 2 B. 3 C.  D.
D. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com