
4. (最后)决定(为)[+to-v][+that]
He concluded that he would wait a little longer.
他决定再等一会儿。
He concluded to quit on pay day.
他决定在发薪水这天辞职。
vi.
结束,终了[(+with)]
The meeting concluded after two hours.
两小时后会议结束了。
Impressive as the record is, it fades next to the story of Armstrong’s struggle against disease.
as引导让步状从,句子倒装。
Angry as he was, he listened to me patiently.
他很恼怒,却能耐心地听我说话。
Strange as it seems, it is so.
看似不可思议,事实却是如此。
fade
vi.
3. 缔结(条约)[(+with)]
2. 推断出,断定 [+that]
What can you conclude from these observations?
你从这些观察中能得出什么结论?
1. 结束[(+by/with)]
We concluded our meeting at 9 o’clock.
我们九点钟结束了会议。
22.(本题满分14分)
解:(Ⅰ)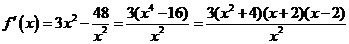 , …………2分
, …………2分
由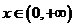 ,得,
,得,
当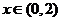 时,
时,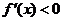 ,
,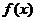 单调递减;
单调递减;
当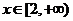 时,
时,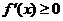 ,
,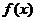 单调递增. …………………………4分
单调递增. …………………………4分
∴ 当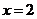 时,
时,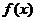 取得最小值
取得最小值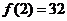 ,
,
即对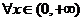 ,
,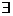 常数
常数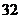 ,都有
,都有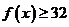 成立,
成立,
所以,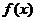 在
在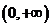 上有下界. ……………………………………………6分
上有下界. ……………………………………………6分
(Ⅱ)由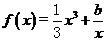 ,知
,知
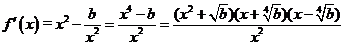 …………………8分
…………………8分
由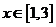 ,知
,知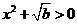 ,
,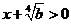 ,
,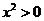
所以,当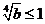 ,即
,即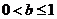 时,
时,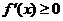 ,
,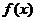 在
在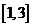 上单调递增;
上单调递增;
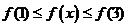 ,即
,即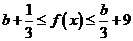 恒成立,
恒成立,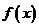 在
在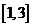 上是有界函数;
上是有界函数;
当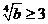 ,即
,即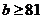 时,
时,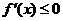 ,
,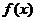 在
在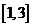 上单调递减;
上单调递减;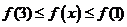 ,即
,即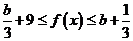 恒成立,
恒成立,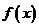 在
在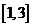 上是有界函数;………………11分
上是有界函数;………………11分
当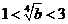 ,即
,即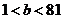 时,有
时,有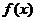 在
在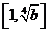 上单调递减;在
上单调递减;在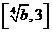 上单调递增,且
上单调递增,且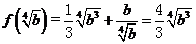 ,
,
从而当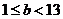 时,
时,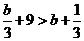 ,
,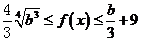 恒成立,
恒成立,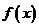 在
在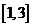 上是有界函数;
上是有界函数;
当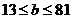 时,
时,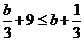 ,
,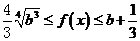 恒成立,
恒成立,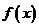 在
在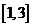 上是有界函数.
……………………………………………………………13分
上是有界函数.
……………………………………………………………13分
综上可知,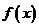 在
在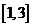 上是有界函数.
上是有界函数.
且当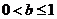 时,下界为
时,下界为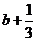 ;当
;当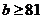 时,下界为
时,下界为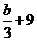 ;当
;当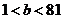 时,下界为
时,下界为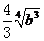 . ………………………………………………………………………………14分
. ………………………………………………………………………………14分
21.(本题满分12分)
解:(Ⅰ)将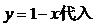
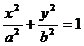 得
得 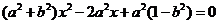
由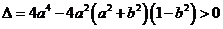 得
得 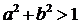
设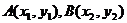 ,则
,则
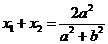 ,
,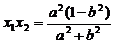 ①……………………………2分
①……………………………2分
∵
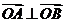 ∴
∴ 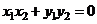
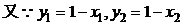
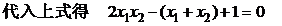 ②
②
将①代入②式,整理得:
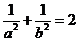 ……………………………4分
……………………………4分
∵ 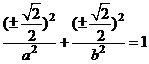
∴ 椭圆过四个定点:
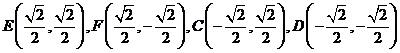 …5分
…5分
∵ 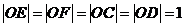
∴ 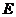 、
、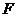 、
、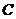 、
、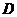 四点在圆
四点在圆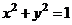 上. ……………………… 7分
上. ……………………… 7分
(Ⅱ)设椭圆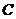 的右焦点为
的右焦点为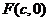 ,
,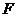 关于直线
关于直线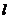 的对称点为
的对称点为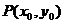 ,
,
则 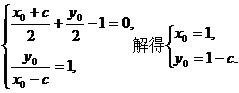 ……………………………8分
……………………………8分
∵ 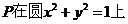 ∴
∴ 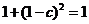 解得
解得 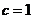 ……9分
……9分
由(I)得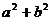 =
=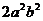 又
又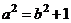
∴ 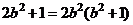 解得
解得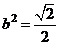 从而
从而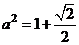
故所求椭圆方程为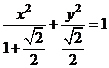 . ………………………12分
. ………………………12分
20.(本题满分12分)
解:(Ⅰ)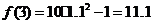 (元); …………………………………………3分
(元); …………………………………………3分
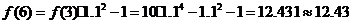 (元).……………6分
(元).……………6分
(Ⅱ)因为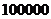 元可买某股票
元可买某股票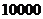 股,又6个月后每股价格为
股,又6个月后每股价格为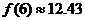 (元),所以,总盈利为
(元),所以,总盈利为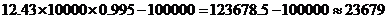 (元).
(元).
答:6个月后盈利为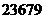 元.……………………………………………………………12分
元.……………………………………………………………12分
19.(本题满分12分)
解:(Ⅰ)依题意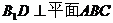 ,∴
,∴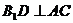
又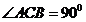 ,∴
,∴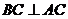 ,
,
而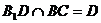 ,∴
,∴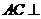 平面
平面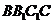 . ……………………………………………4分
. ……………………………………………4分
(Ⅱ)∵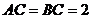 ,
,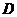 为
为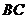 的中点,∴
的中点,∴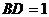
又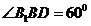 ∴在
∴在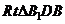 中,
中,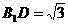 ,
,
而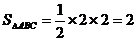 , ………………………………………………………………7分
, ………………………………………………………………7分
∴斜三棱柱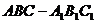 的体积
的体积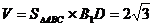 .……………………………8分
.……………………………8分
(Ⅲ)由(Ⅰ)知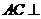 平面
平面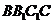 ,又
,又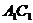 ∥
∥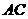 ∴
∴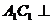 平面
平面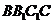 ,
,
∴四棱锥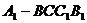 的高
的高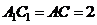
由(Ⅱ)知,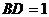 ,
,
而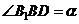 ,∴在
,∴在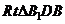 中,
中,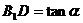 ,
,
∴底面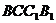 的面积
的面积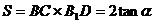 , ……………………………………10分
, ……………………………………10分
依题意: 四棱锥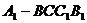 的体积
的体积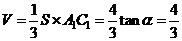 ,
,
∴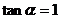 ,又
,又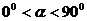 ,∴
,∴ 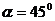 ,
,
于是,当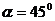 时,四棱锥
时,四棱锥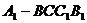 的体积为
的体积为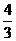 .………………………………12分
.………………………………12分
18.(本题满分12分)
解:(Ⅰ)从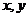 各取一个数组成数对
各取一个数组成数对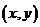 共有
共有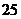 对, ……………………………2分
对, ……………………………2分
其中满足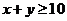 的有(6,4),(6,5),(7,3),(7,4),(7,5),(8,2),(8,3),(8,4),(8,5)共9对 ………………………………………………………4分
的有(6,4),(6,5),(7,3),(7,4),(7,5),(8,2),(8,3),(8,4),(8,5)共9对 ………………………………………………………4分
故所求的概率为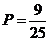 ………………………………………………………6分
………………………………………………………6分
(Ⅱ)用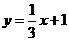 作为拟合直线时,所得
作为拟合直线时,所得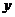 值与
值与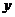 的实际值的差的平方和为
的实际值的差的平方和为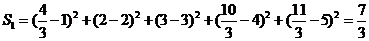 ……………8分
……………8分
用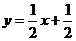 作为拟合直线时,所得
作为拟合直线时,所得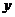 值与
值与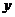 的实际值的差的平方和为
的实际值的差的平方和为
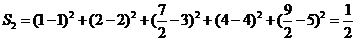 ………………10分
………………10分
∵ 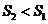 ,故用直线
,故用直线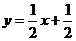 拟合程度更好.
…………………………………12分
拟合程度更好.
…………………………………12分
17.(本题满分12分)
解:(Ⅰ)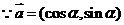 ,
, 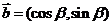 ,
,
∴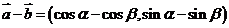 . ……………………………………………1分
. ……………………………………………1分
又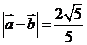 , ∴
, ∴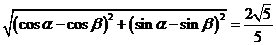 , …………3分
, …………3分
即 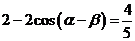 , ∴
, ∴ 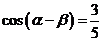 . …………………………5分
. …………………………5分
(Ⅱ)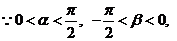 , ∴
, ∴ 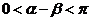
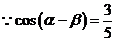 , ∴
, ∴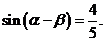 …………………………………………7分
…………………………………………7分
又 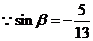 , ∴
, ∴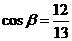 , …………………………………………9分
, …………………………………………9分
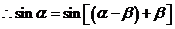
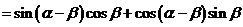
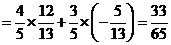 . …………………………………………12分
. …………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com