
若平面内一个动点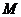 到一个定点
到一个定点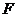 和一条定直线
和一条定直线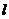 的距离之比等于一个常数
的距离之比等于一个常数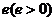 则动点的轨迹为圆锥曲线。其中定点
则动点的轨迹为圆锥曲线。其中定点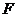 为焦点,定直线
为焦点,定直线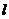 为准线,
为准线,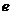 为离心率。当
为离心率。当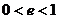 时,轨迹为椭圆;当
时,轨迹为椭圆;当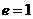 时,轨迹为抛物线;当
时,轨迹为抛物线;当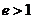 时,轨迹为双曲线。
时,轨迹为双曲线。
(1)抛物线的定义:平面内与一个定点的距离等于到一条定直线的距离点的轨迹。
其中:定点为抛物线的焦点,定直线叫做准线。
(2)抛物线的标准方程、图象及几何性质: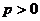
|
|
焦点在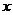 轴上, 轴上,开口向右 |
焦点在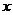 轴上, 轴上,开口向左 |
焦点在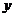 轴上, 轴上,开口向上 |
焦点在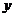 轴上, 轴上,开口向下 |
|
标准方程 |
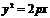 |
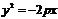 |
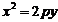 |
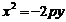 |
|
图 形 |
 |
 |
 |
 |
|
顶 点 |
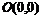 |
|||
|
对称轴 |
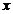 轴 轴 |
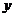 轴 轴 |
||
|
焦 点 |
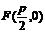 |
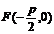 |
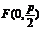 |
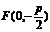 |
|
离心率 |
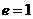 |
|||
|
准 线 |
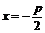 |
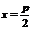 |
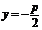 |
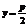 |
|
通 径 |
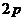 |
|||
|
焦半径 |
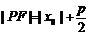 |
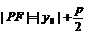 |
||
|
焦点弦 |
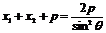 (当 (当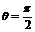 时,为 时,为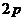 --通径) --通径) |
|||
|
焦准距 |
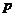 |
(1)双曲线的定义:平面内与两个定点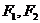 的距离的差的绝对值等于常数(小于
的距离的差的绝对值等于常数(小于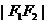 )的点的轨迹。
)的点的轨迹。
第二定义:平面内与一个定点的距离和到一条定直线的距离的比是常数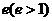 的点的轨迹。
的点的轨迹。
其中:两个定点叫做双曲线的焦点,焦点间的距离叫做焦距;定直线叫做准线。
常数叫做离心率。
注意: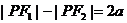 与
与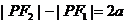 (
(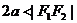 )表示双曲线的一支。
)表示双曲线的一支。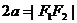 表示两条射线;
表示两条射线;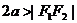 没有轨迹;
没有轨迹;
(2)双曲线的标准方程、图象及几何性质:
|
|
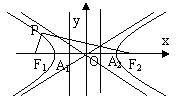
中心在原点,焦点在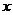 轴上 轴上 |
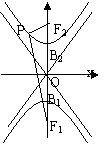
中心在原点,焦点在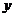 轴上 轴上 |
||
|
标准方程 |
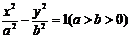 |
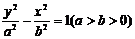 |
||
|
图 形 |
 |
|
||
|
顶 点 |
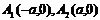 |
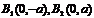 |
||
|
对称轴 |
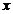 轴, 轴,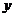 轴;虚轴为 轴;虚轴为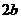 ,实轴为 ,实轴为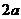 |
|||
|
焦 点 |
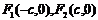 |
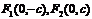 |
||
|
焦 距 |
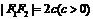 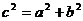 |
|||
|
离心率 |
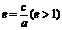 (离心率越大,开口越大) (离心率越大,开口越大) |
|||
|
准 线 |
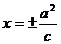 |
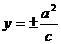 |
||
|
渐近线 |
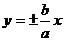 |
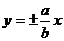 |
||
|
通 径 |
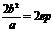 ( (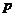 为焦准距) 为焦准距) |
|||
|
焦半径 |
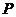 在左支 在左支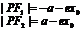 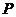 在右支 在右支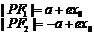 |
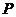 在下支 在下支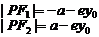 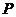 在上支 在上支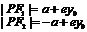 |
||
|
焦准距 |
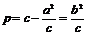 |
(3)双曲线的渐近线:
①求双曲线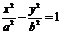 的渐近线,可令其右边的1为0,即得
的渐近线,可令其右边的1为0,即得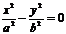 ,因式分解得到。
,因式分解得到。
②与双曲线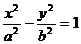 共渐近线的双曲线系方程是
共渐近线的双曲线系方程是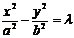 ;
;
(4)等轴双曲线为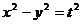 ,其离心率为
,其离心率为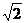
(1)椭圆的定义:平面内与两个定点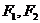 的距离的和等于常数(大于
的距离的和等于常数(大于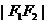 )的点的轨迹。
)的点的轨迹。
第二定义:平面内与一个定点的距离和到一条定直线的距离的比是常数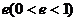 的点的轨迹。
的点的轨迹。
其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距;定直线叫做准线。
常数叫做离心率。
注意: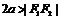 表示椭圆;
表示椭圆;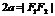 表示线段
表示线段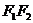 ;
;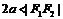 没有轨迹;
没有轨迹;
(2)椭圆的标准方程、图象及几何性质:
|
|
中心在原点,焦点在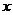 轴上 轴上 |
中心在原点,焦点在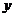 轴上 轴上 |
||
|
标准方程 |
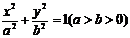 |
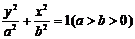 |
||
|
参数方程 |
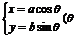 为参数) 为参数) |
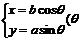 为参数) 为参数) |
||
|
图 形 |
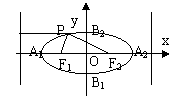 |
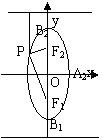
|
||
|
顶 点 |
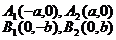 |
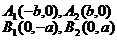 |
||
|
对称轴 |
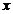 轴, 轴,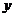 轴;短轴为 轴;短轴为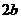 ,长轴为 ,长轴为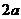 |
|||
|
焦 点 |
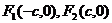 |
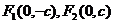 |
||
|
焦 距 |
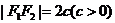 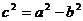 |
|||
|
离心率 |
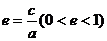 (离心率越大,椭圆越扁) (离心率越大,椭圆越扁) |
|||
|
准 线 |
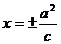 |
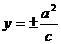 |
||
|
通 径 |
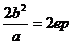 ( (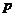 为焦准距) 为焦准距) |
|||
|
焦半径 |
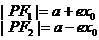 |
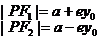 |
||
|
焦点弦 |
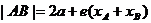 仅与它的中点的横坐标有关 |
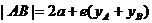 仅与它的中点的纵坐标有关 |
||
|
焦准距 |
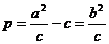 |
圆锥曲线部分
10. 如图,已知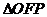 的面积为m,且
的面积为m,且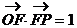
(I)若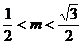 ,求向量
,求向量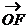 与
与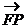 的夹角的取值范围;
的夹角的取值范围;
(II)设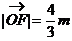 ,且
,且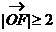 。若以O为中心,F为焦点的椭圆经过点P,当
。若以O为中心,F为焦点的椭圆经过点P,当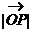 取得最小值时,求此椭圆的方程。
取得最小值时,求此椭圆的方程。
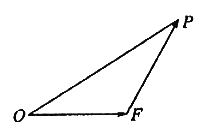
解:(I)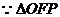 的面积为m,设向量
的面积为m,设向量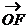 与
与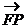 的夹角为
的夹角为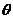
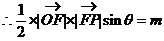 ①
①
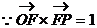 ,
,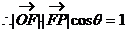 ②
②
由①、②得: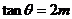
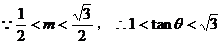
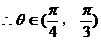
即向量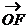 与
与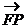 的夹角
的夹角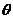 的取值范围为
的取值范围为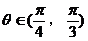 6分
6分
(II)如图,以O为原点,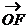 所在直线为x轴建立直角坐标系
所在直线为x轴建立直角坐标系
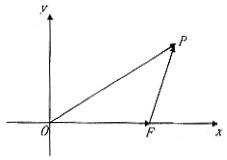
设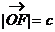 ,P点坐标为(x0,y0)
,P点坐标为(x0,y0)
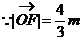
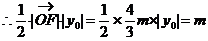 ,
,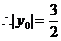
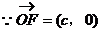 ,
,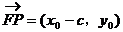 ,
,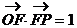
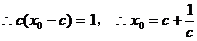
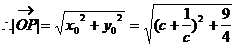
设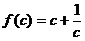 ,当
,当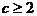 时,任取
时,任取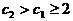
有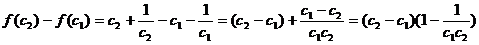
当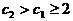 时,
时,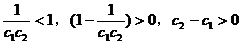
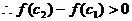 ,
,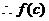 在[2,
在[2,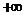 )上是增函数
)上是增函数
 当
当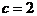 时,
时,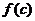 为最小,从而
为最小,从而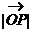 为最小,此时P(
为最小,此时P(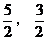 )
)
设椭圆的方程为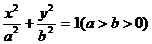 ,则
,则
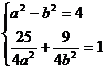
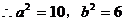
故椭圆的方程为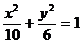
(答:C);(答:双曲线的左支)(答:2)
(答: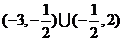 );(答:
);(答: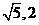 )(答:
)(答: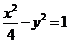 );(答:
);(答: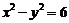 )(答:
)(答: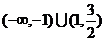 )(答:3或
)(答:3或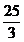 );(答:
);(答: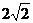 )(答:
)(答: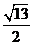 或
或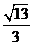 );(答:4或
);(答:4或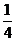 );(答:
);(答: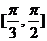 );(答:
);(答: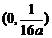 );(答:(-
);(答:(- ,-1))(答:[1,5)∪(5,+∞));(答:3);(答:2);(答:
,-1))(答:[1,5)∪(5,+∞));(答:3);(答:2);(答: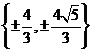 );(答:相离);(答:1);(填大于、小于或等于) (答:等于);(答:
);(答:相离);(答:1);(填大于、小于或等于) (答:等于);(答: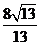 );(答:①
);(答:①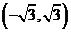 ;②
;②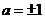 );(答:
);(答: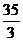 );(答:
);(答: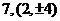 );(答:
);(答: );(答:2);(答:
);(答:2);(答: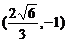 );(答:6);(答:
);(答:6);(答: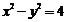 );(答:
);(答: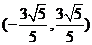 );(答:
);(答: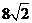 );(答:
);(答: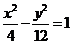 );(答:8);(答:3);(答:
);(答:8);(答:3);(答: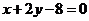 );(答:
);(答: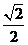 );(答:
);(答: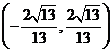 )(答:
)(答: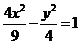 )(答:
)(答: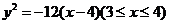 或
或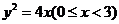 )(答:
)(答: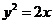 );(答:
);(答: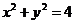 );(答:
);(答: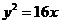 );(答:双曲线的一支);(答:
);(答:双曲线的一支);(答: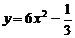 );(答:
);(答: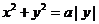 );(答:
);(答: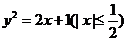 );(答:
);(答: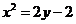 );(答:(1)略;(2)
);(答:(1)略;(2)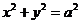 ;(3)当
;(3)当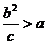 时不存在;当
时不存在;当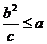 时存在,此时∠F1MF2=2)
时存在,此时∠F1MF2=2)
9. 已知抛物线方程为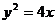 ,过点
,过点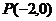 的直线AB交抛物线于点A、B。
的直线AB交抛物线于点A、B。
(1)若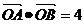 ,求直线AB的方程;
,求直线AB的方程;
(2)若线段AB的垂直平分线交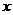 轴于点
轴于点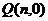 ,求
,求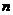 的取值范围。
的取值范围。
解:设直线AB的方程为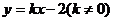 ,点
,点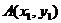 ,
,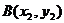
把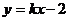 代入抛物线方程可得:
代入抛物线方程可得: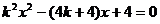
∴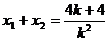 ,
,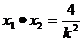
∴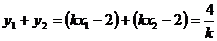 ,
,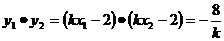
(1)∵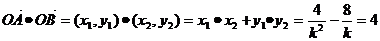
∴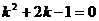
∴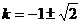
又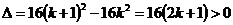
∴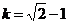
∴直线AB的方程为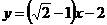 。
。
(2)设线段AB的中点C的坐标为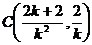
则直线CQ的方程为: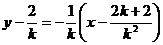
令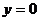 ,则
,则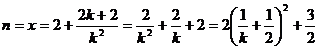
又由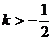 且
且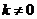 得:
得: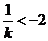 或
或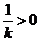
则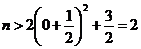
∴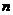 的取值范围为
的取值范围为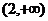 。
。
7. 已知:过点A(1,0)且互相垂直的两动直线与直线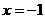 分别相交于E、F两点,O为坐标原点,动点P满足
分别相交于E、F两点,O为坐标原点,动点P满足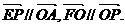
(1)求动点P的轨迹C的方程;
(2)若直线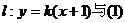 中轨迹C交于M、N两点,且
中轨迹C交于M、N两点,且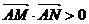 ,求k的取值范围.
,求k的取值范围.
解:(1)设点P的坐标是(x,y)
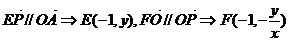 ………………2分
………………2分
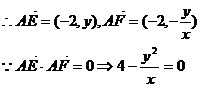
∴点P轨迹方程是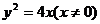 ………………6分
………………6分
(2)由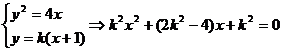
有两交点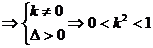 ………………8分
………………8分
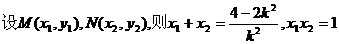 ………………9分
………………9分
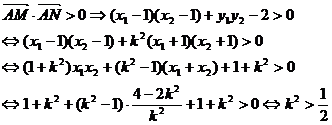
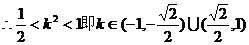
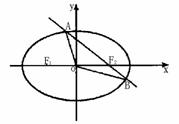
6. 圆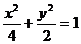 的左、右焦点分别为F1,F2,直线
的左、右焦点分别为F1,F2,直线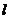 过F2与椭圆相交于A、B两点,O为坐标原点.
过F2与椭圆相交于A、B两点,O为坐标原点.
(1)当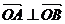 时,求直线
时,求直线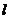 的方程;
的方程;
(2)当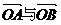 的夹角为120°时,求直线
的夹角为120°时,求直线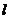 的斜率k的值.
的斜率k的值.
 解:(1)
解:(1)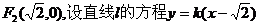
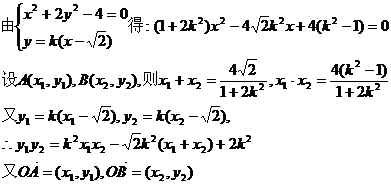
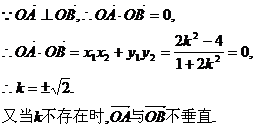
∴所求直线方程为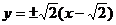 .
.
(2)又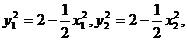
|
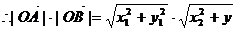
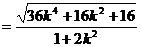
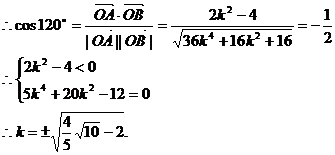
2.解Ⅰ)设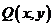 ,则
,则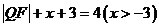 ,即:
,即:
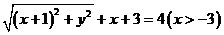 ,化简得:
,化简得: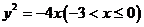 .
.
所以,动点Q的轨迹为抛物线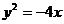 位于直线
位于直线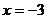 右侧的部分.
右侧的部分.
(Ⅱ)因为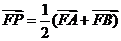 ,所以,P为AB中点;又因为
,所以,P为AB中点;又因为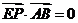 ,且
,且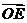 =(
=(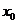 ,0),
,0),
所以,点E为线段AB垂直平分线与x轴焦点.
由题可知:直线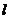 与
与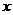 轴不垂直,所以可设直线
轴不垂直,所以可设直线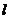 的方程为
的方程为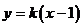 ,
,
代入轨迹C的方程得到: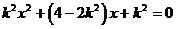
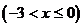 (*)
(*)
设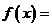
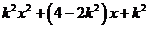 ,要使得
,要使得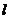 与C有两个不同交点,需且只需
与C有两个不同交点,需且只需
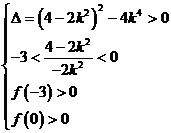 解之得:
解之得: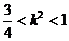
由(*)式得: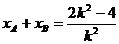 ,所以,AB中点P的坐标为:
,所以,AB中点P的坐标为:
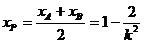 ,
,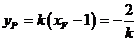 .所以,直线EP的方程为
.所以,直线EP的方程为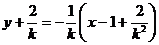
令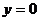 得到点E的横坐标为
得到点E的横坐标为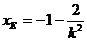 .因为
.因为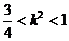 ,所以,
,所以,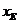 ∈(
∈(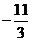 ,-3).
,-3).
(Ⅲ)不可能.要使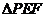 成为以EF为底的等腰三角形,需且只需
成为以EF为底的等腰三角形,需且只需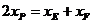 ,
,
即: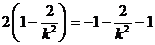 ,解得:
,解得: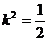 .
.
另一方面,要使直线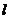 满足(2)的条件,需要
满足(2)的条件,需要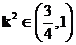 ,
,
所以,不可能使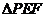 成为以EF为底的等腰三角形.
成为以EF为底的等腰三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com