19．图是质谱仪工作原理的示意图。带电粒子a、b经电压U加速(在A点初速度为零)后，进入磁感应强度为B的匀强磁场做匀速圆周运动，最后分别打在感光板S上的x₁、x₂处。图中半圆形的虚线分别表示带电粒子a、b所通过的路径，则

A．a的质量一定大于b的质量

B．a的电荷量一定大于b的电荷量

C．a运动的时间大于b运动的时间

D．a的比荷(q _a /m_a)大于b的比荷(q_b /m_b)

18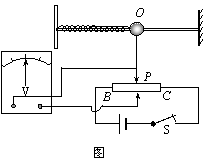．将如图所示装置安装在沿直轨道运动的火车车厢中，使杆沿轨道方向固定，就可以对火车运动的加速度进行检测。闭合开关S，当系统静止时，穿在光滑绝缘杆上的小球停在O点，固定在小球上的变阻器滑片停在变阻器BC的正中央，此时，电压表指针指在表盘刻度中央。当火车在水平方向有加速度时，小球在光滑绝缘杆上移动，滑片P随之在变阻器上移动，电压表指针发生偏转。已知，当火车向右加速运动时，电压表的指针向左偏。则:

A. 若火车向右做减速运动，小球在O点右侧，电压表指针向左偏

B. 若火车向左做加速运动，小球在O点左侧，电压表指针向右偏

C. 若火车向左做减速运动，小球在O点左侧，电压表指针向左偏

D. 若火车向右做加速运动，小球在O点右侧，电压表指针向左偏

17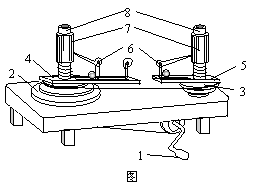． 向心力演示器如图所示。转动手柄1，可使变速塔轮2和3以及长槽4和短槽5随之匀速转动。皮带分别套在塔轮2和3上的不同圆盘上，可使两个槽内的小球分别以几种不同的角速度做匀速圆周运动。小球做圆周运动的向心力由横臂6的挡板对小球的压力提供，球对挡板的反作用力，通过横臂的杠杆使弹簧测力套筒7下降，从而露出标尺8，标尺8上露出的红白相间等分格子的多少可以显示出两个球所受向心力的大小。现将小球分别放在两边的槽内，为探究小球受到的向心力大小与角速度的关系，下列做法正确的是　　

　A. 在小球运动半径相等的情况下，用质量相同的钢球做实验

　B. 在小球运动半径相等的情况下，用质量不同的钢球做实验

　C. 在小球运动半径不等的情况下，用质量不同的钢球做实验

　D. 在小球运动半径不等的情况下，用质量相同的钢球做实验

16.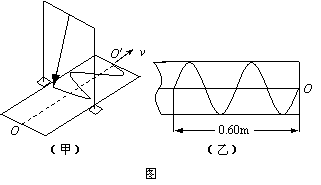 如图(甲)所示是用沙摆演示振动图象的实验装置，此装置可视为摆长为L的单摆，沙摆的运动可看作简谐运动，实验时在木板上留下图(甲)所示的结果。若用手拉木板做匀速运动，速度大小是0.20m/s。图(乙)所示的一段木板的长度是0.60m，那么这次实验所用沙摆对应的单摆长约为

　 　A. 2.0m 　　B. 1.5m　　

C. 1.0m　 　D. 0.56m

15．分子间有相互作用的势能，规定两分子相距无穷远时分子势能为零，并已知两分子相距r₀时分子间的引力与斥力大小相等。设分子a 和分子b从相距无穷远处分别以一定的初速度在同一直线上相向运动，直到它们之间的距离达到最小。在此过程中下列说法正确的是

A. a和b之间的势能先增大，后减小

B. a和b的总动能先增大，后减小

C. 两分子相距r₀时， a和b的加速度均不为零

D. 两分子相距r₀时， a和b之间的势能大于零

14．关于天然放射现象，下列说法中正确的是　　

A．β衰变说明原子核里有电子

B．某原子核经过一次α衰变和两次β衰变后，核内中子数减少4个

C．放射性物质的温度升高，其半衰期将缩短

D．γ射线的电离作用很强，可用来消除有害静电

13．在下列各组光学实验现象或事实中，都能说明光具有波动性的一组是　 　

A．泊松亮斑、雨后空中出现的彩虹

B. 水面上的油膜呈现彩色、用光导纤维传播信号

C. 光的双缝干涉现象、偏振现象

D. 日食、光电效应现象

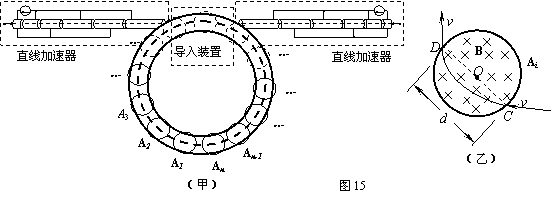
24．(20分)如图(甲)所示为一种研究高能粒子相互作用的装置，两个直线加速器均由k个长度逐个增长的金属圆筒组成(整个装置处于真空中。图中只画出了6个圆筒，作为示意)，它们沿中心轴线排列成一串，各个圆筒相间地连接到频率为f、最大电压值为U的正弦交流电源的两端。设金属圆筒内部没有电场，且每个圆筒间的缝隙宽度很小，带电粒子穿过缝隙的时间可忽略不计。为达到最佳加速效果，应当调节至粒子穿过每个圆筒的时间恰为交流电的半个周期，粒子每次通过圆筒间缝隙时，都恰为交流电压的峰值。

质量为m、电荷量为e的正、负电子分别经过直线加速器加速后，从左、右两侧被导入装置送入位于水平面内的圆环形真空管道，且被导入的速度方向与圆环形管道中粗虚线相切。在管道内控制电子转弯的是一系列圆形电磁铁，即图中的A₁、A₂、A₃……A_n，共n个，均匀分布在整个圆周上(图中只示意性地用细实线和细虚线了几个)，每个电磁铁内的磁场都是磁感应强度和方向均相同的匀强磁场，磁场区域都是直径为d的圆形。改变电磁铁内电流的大小，就可改变磁场的磁感应强度，从而改变电子偏转的角度。经过精确的调整，可使电子在环形管道中沿图中粗虚线所示的轨迹运动，这时电子经过每个电磁铁时射入点和射出点都在电磁铁的一条直径的两端，如图(乙)所示。这就为实现正、负电子的对撞作好了准备。

(1)若正电子进入第一个圆筒的开口时的速度为v₀，且此时第一、二两个圆筒的电势差为U，正电子进入第二个圆筒时的速率多大？

(2)正、负电子对撞时的速度多大？

(3)为使正电子进入圆形磁场时获得最大动能，各个圆筒的长度应满足什么条件？

(4)正电子通过一个圆形磁场所用的时间是多少？

(1)设正电子进入第二个圆筒时的速率为v₁，根据动能定理

　　 eU=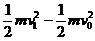

　　 解得：v₁=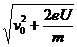

(2)正、负电子对撞时的动能等于进入第k个圆筒时的动能E_k，根据动能定理

　　 (k-1)eU=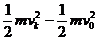

　 　解得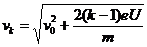　　

(3)设正电子进入第N个圆筒的速率为v_N-1，第N个圆筒的长度为L_N，则

　　 L_N=v_N-1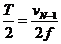

　　 由动能定理得

　　 (N-1)eU=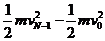

　　 解得：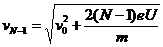

　　 第N个圆筒的长度应满足的条件是：

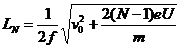　(N=1、2、3……k)

　(4)设电子经过1个电磁铁的圆形磁场区过程中偏转角度为θ ，则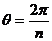

由图可知，电子射入匀强磁场区时的速度与通过射入点的磁场直径夹角为θ/ 2

　　 电子在磁场区内作圆运动，洛仑兹力是向心力

∴　　 　

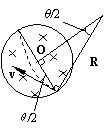
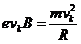
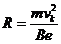
根据几何关系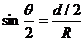　

　　　　　 解出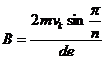　

设正电子通过一个圆形磁场所用的时间是t，则，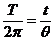

　而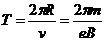

所以，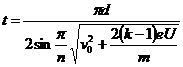

23．(18分)如图所示，一轻质弹簧竖直固定在地面上，上面连接一个质量m₁=1.0kg的物体A，平衡时物体下表面距地面h₁=0.40m，弹簧的弹性势能E_P=0.50J。在距物体m₁正上方高为h=0.45m处有一个质量m₂=1.0kg的物体B自由下落后，与弹簧上面的物体m₁碰撞(两物体粘连)并立即以相同的速度运动，当弹簧压缩量最大时，物体距地面的高度h₂=6.55cm。g=10m/s²。求：

(1)弹簧不受作用力时的自然长度；

(2)两物体做简谐运动的振动振幅;

(3)两物体运动到最高点时的弹性势能。

(1)设物体A放在弹簧上平衡时对弹簧的压缩量为x₁，根据能量守恒有

　　 m₁gx₁=2E_p

　　 解得：x₁=0.10m

　　 所以，弹簧不受作用力时的自然长度x₀=h₁+x₁=0.50m

(2)设物体A静止在上端时的弹簧的压缩量为x₁,

　　 x₁=x₀-h₁=0.10m

设弹簧劲度系数为k，根据胡克定律有

　　 m₁g=kx₁　　 解得：k=100N/m

两物体向上运动过程中，弹簧弹力等于两物体总重力时具有最大速度，

设此时弹簧的压缩量为x₂，则

(m₁+ m₂)g=kx₂，

解得：x₂=0.20m，设此时弹簧的长度为l­₂，则

l₂=x₀-x₂

解得：l₂=0.30m

当弹簧压缩量最大时，是两物体振动最大位移处，此时弹簧长度为h₂=6.55cm

　　 两物体做简谐运动的振幅A=l₂-h₂ =23.45cm

(3)设物体B自由下落与物体A相碰时的速度为v₁，则

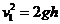
解得：v₁=3.0m/s，

　　 设A与B碰撞结束瞬间的速度为v₂，根据动量守恒

m₂ v₁=(m₁+ m₂)v₂，

解得：v₂=1.5 m/s，

　　 设此时A、B两物体和弹簧具有的总机械能为E₁

　　 E₁=E_p+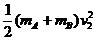

　　 设两物体向上运动过程中在弹簧达到原长时的速度为v₃，

从碰后到弹簧达到原长过程，物体和弹簧组成的系统机械能守恒，

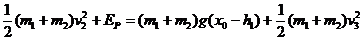
解得：v₃=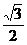 m/s=0.87 m/s

设两物体上升到最高点是弹簧具有的弹性势能为E_p1

根据机械能能守恒

E_p1+(m₁+m₂)g(A-0.20)=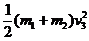

解得：E_p1=6.0×10^-2J。

23．(18分)如图所示，一轻质弹簧竖直固定在地面上，上面连接一个质量m₁=1.0kg的物体A，平衡时物体下表面距地面h₁= 40cm，弹簧的弹性势能E₀=0.50J。在距物体m₁正上方高为h= 45cm处有一个质量m₂=1.0kg的物体B自由下落后，与物体A碰撞并立即以相同的速度运动(两物体粘连在一起)，当弹簧压缩量最大时，物体距地面的高度h₂=6.55cm。g=10m/s²。

(1)已知弹簧的形变(拉伸或者压缩)量为x时的弹性势能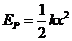，式中k为弹簧的劲度系数。求弹簧不受作用力时的自然长度l₀；

(2)求两物体做简谐运动的振幅;

(3)求两物体运动到最高点时的弹性势能。

(1)设物体A在弹簧上平衡时弹簧的压缩量为x₁，弹簧的劲度系数为k

根据力的平衡条件有　　　　 m₁g=k x₁

　　　　 而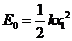

　　 解得：k=100N/m，　 x₁=0.10m

　　 所以，弹簧不受作用力时的自然长度l₀=h₁+x₁=0.50m

(2)两物体运动过程中，弹簧弹力等于两物体总重力时具有最大速度，此位置就是两物体粘合后做简谐运动的平衡位置

设在平衡位置弹簧的压缩量为x₂，则　 (m₁+ m₂)g=kx₂， 解得：x₂=0.20m，

设此时弹簧的长度为l₂，则　　 l₂=l₀-x₂　　 ,解得：l₂=0.30m ,

当弹簧压缩量最大时，是两物体振动最大位移处，此时弹簧长度为h₂=6.55cm

　　 两物体做简谐运动的振幅A=l₂-h₂ =23.45cm

(3)设物体B自由下落与物体A相碰时的速度为v₁，则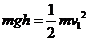　　

解得：v₁=3.0m/s，

　　 设A与B碰撞结束瞬间的速度为v₂，根据动量守恒　 m₂ v₁=(m₁+ m₂)v₂，

解得：v₂=1.5 m/s，

　　 由简谐运动的对称性，两物体向上运动过程达到最高点时，速度为零，弹簧长度为l₂+A=53.45cm

碰后两物体和弹簧组成的系统机械能守恒，设两物体运动到最高点时的弹性势能E_P，则　　　

解得E_P＝6.0×10^-2J。

23B. 较难的设问