
4.答案:B
解析:方法一:可利用特殊值法,令k=-2,-1,0,1,2可得
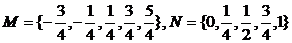
∴M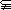 N
N
方法二:集合M的元素为: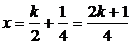 (k∈Z),集合N的元素为:x=
(k∈Z),集合N的元素为:x=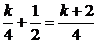 (k∈Z),而2k+1为奇数,k+2为整数,因此M
(k∈Z),而2k+1为奇数,k+2为整数,因此M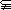 N.∴M
N.∴M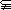 N
N
3.答案:C
解析:M={2,3}或M={1,2,3}
评述:因为M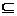 {1,2,3},因此M必为集合{1,2,3}的子集,同时含元素2,3.
{1,2,3},因此M必为集合{1,2,3}的子集,同时含元素2,3.
2.答案:C
解析:依题意可得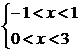 ,可得0<x<1.
,可得0<x<1.
1.答案:C
解析:∵|ax+2|<6,∴-6<ax+2<6,-8<ax<4
当a>0时,有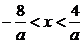 ,而已知原不等式的解集为(-1,2),所以有:
,而已知原不等式的解集为(-1,2),所以有:
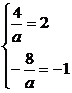 .此方程无解(舍去).
.此方程无解(舍去).
当a<0时,有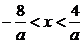 ,所以有
,所以有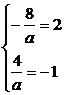
解得a=-4,当a=0时,原不等式的解集为R,与题设不符(舍去),故a=-4.
评述:本题主要考查绝对值不等式的解法,方程的根与不等式解集的关系,考查了分类讨论的数学思想方法及逻辑思维能力,此题也可以利用选项的值代入原不等式,去寻找满足题设条件的a的值.
32.(1999上海,17)设集合A={x||x-a|<2},B={x|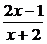 <1},若A
<1},若A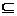 B,求实数a的取值范围.
B,求实数a的取值范围.
●答案解析
31.(2000上海春,17)已知R为全集,A={x|log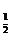 (3-x)≥-2},B={x|
(3-x)≥-2},B={x|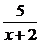 ≥1},求
≥1},求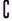 RA∩B.
RA∩B.
30.(2003上海春,17)解不等式组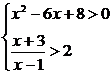 .
.
29.(1999全国,18)α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:
①m⊥n ②α⊥β ③n⊥β ④m⊥α
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题:_____.
28.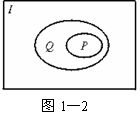 (2000上海春,12)设I是全集,非空集合P、Q满足P
(2000上海春,12)设I是全集,非空集合P、Q满足P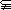 Q
Q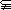 I.若含P、Q的一个集合运算表达式,使运算结果为空集
I.若含P、Q的一个集合运算表达式,使运算结果为空集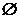 ,则这个运算表达式可以是
(只要写出一个表达式).
,则这个运算表达式可以是
(只要写出一个表达式).
27.(2001天津理,15)在空间中
①若四点不共面,则这四点中任何三点都不共线;
②若两条直线没有公共点,则这两条直线是异面直线.
以上两个命题中,逆命题为真命题的是_____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com