参考文献：

1] 钟绍春，姜雁秋：《信息技术与课程整合的模型和方法》 中国电化教育，2003(9)

通过一段时间的教学，笔者发现，利用多媒体辅助教学，在某些方面弥补了传统教学所无法解决的一些难题，而这些难题对训练学生思维起着重要的作用.下面给出一个经典例子予以说明如何训练学生的思维？

教师：判断此命题真假(05年江西高考卷第16小题)：

过定圆C上一定点A作圆的动弦AB，O为坐标原点，若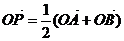，则动点P的轨迹为椭圆.

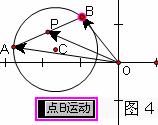
笔者课堂上在《几何画板》软件中即时制作了如图4满足题意的小课件，单击“点B运动”的按钮得到从动点P也随着运动，多数同学们观察到点P的轨迹似乎是一个圆.究竟是不是圆呢？如何说明点P的轨迹是椭圆还是圆呢？因此进行下一步的训练：

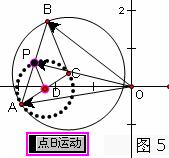
教师：选中点P后单击[显示]工具栏“追踪点”，接着单击“点B运动”按钮，得到点P轨迹(如图5).点P的轨迹似乎是圆，请同学们充分调动各自的聪明才智，认真思考后阐述点P的轨迹是什么图形？

学生A：设定圆C的方程为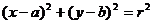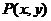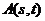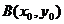：，，，；(a、b、r、s、t均为常数，且) ；

∵；

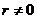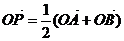
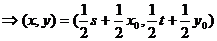
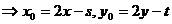又点B在圆C上，把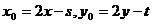代入圆C方程，得：

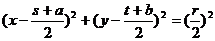，此方程即为点P的轨迹方程.

故点P的轨迹是以点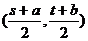为圆心，以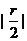为半径的圆.

学生B：由已知得，点P是线段AB的中点；而点C、A均为定点，所以线段AC的中点也为定点，连接PD、BC，则PC是△ABC的中位线，所以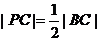(点P满足到定点C的距离等于定长)，即点P的轨迹是以点C为圆心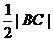，长为半径的圆，故此命题为假.

教师：上面两位同学的解答中可以充分反映同学们思维活动非常活跃，这也是在信息技术的强大功能之下的突出特点.

笔者在上文中通过几个例子论述了利用信息技术(多媒体教学设备，《几何画板》教学软件)“训练”学生的表达能力、创新能力和思维能力.在以上的这些训练中无疑还贯穿了下面的训练：

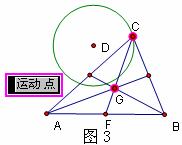教师：下面请同学仔细观察屏幕中动画反映的事实，认真思考后“创新”一个题目，不用给出解答.

(在教师即时制作动画时学生很容易直观地看出其意思，但对读者需作简单说明：点A、B是定点，圆D是一定圆，点C在圆D上运动，点G是△ABC两条中线的交点，即△ABC的重心，主动点C在定圆D上运动，从动点G随之运动)

同学们认真观察之后积极踊跃地写出了他们的“创新”题：

学生E：点A、B是定圆D外的两定点，点C在圆D上运动，点G是△ABC的重心，求动点G的轨迹方程.

学生F：点A、B是两定点，圆D是一定圆，点C在圆D上运动，动点G满足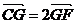，求动点G的轨迹.

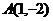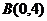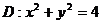学生G：已知点、和圆，点C在圆D上运动，点G是△ABC三条中线的交点，求动点G的轨迹方程.

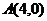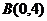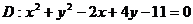学生H：已知点、和圆，点C在圆D上运动，动点G满足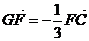，求动点G的轨迹.

……………………

教师对每一位学生的“创新”给以肯定，对不同“创新”加以分析点评.

◆教师：制作点P的动画，并追踪点P得到点P的轨迹如图1(图中黑粗线).根据屏幕中的动画，请说出其意义.

学生A：点P的轨迹是一个圆.

学生B：动点P到定点A的距离等于定值6，故由圆的定义，动点P的轨迹是以点A为圆心，以6为半径的圆.

教师：两位同学回答得都很好.但第二位同学把他所得出结论的理由说得非常清楚.我们再看下一个动画：

◆教师：根据屏幕中的动画，请你用准确语言描述此动画是什么意思？通过什么数学方法验证你的上述判断？(如图2)

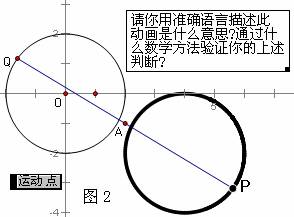学生C：动点P的轨迹似乎是一个圆.

学生D：动点Q在定圆O上运动，点A是一定点，动点P满足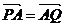，我的判断也是动点P的轨迹是一个圆.

教师：第一位同学回答中说到了“似乎” ，这实际上是通过信息技术的优势得出的一个直觉判断，在数学乃至所有自然科学中，直觉判断确实是发现真理的有效方法.第二位同学观察得较为细致，表达的语言也非常流畅；两位同学的最后判断都说动点P的轨迹是圆，究竟是不是呢？有哪一位同学上来给出文字的论证？

学生D上来在黑板写下了他的文字论证：

不妨设定圆O的方程为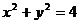：，定点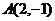，点Q的圆O点的动点，

又设动点，，；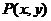

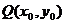
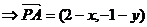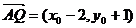由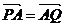

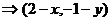
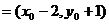
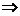
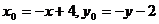
把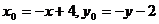代入圆O方程，

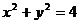即得点P的轨迹方程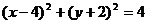：，此方程表示以点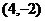为圆心，以2为半径的圆.

20、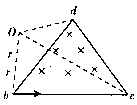(12分)如图所示，在边长为a的等边三角形bcd所围区域内有磁感应强度为B、方向垂直纸面向里的匀强磁场，某一时刻静止于b点处的原子核X发生α衰变，α粒子沿bc方向射入磁场，经磁场偏转后恰好由d射出且与cd边相切．已知α粒子质量为m，电荷量为2e，剩余核的质量为M，衰变过程中释放的核能全部转化为动能，求原子核X的质量．

19、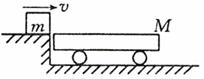(10分)如图所示，质量m=0.5kg的小木块，以v=30m/s的水平速度滑上静止在光滑地面上的平板小车，若小车质量M=2kg，木块与车之间的动摩擦因数μ=0.3，小车足够长，g=10m/s²，

　　 求：(1)木块和小车相对静止时，小车的速度；

　 (2)从木块滑上车到与车相对静止所用的时间。

18、(10分)一群氢原子处于量子数n=4能级状态，氢原子的能级图如图所示，则：(1)氢原子可能发射几种频率的光子？

(2)氢原子由量子数n=4的能级跃迁到n=2的能级时辐射光子的能量是多少电子伏？

(3)用(2)中的光子照射下表中几种金属，哪些金属能发生光电效应？发生光电效应时，发射光电子的最大初动能是多大？

17、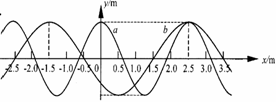(3分)有两列简谐横波a、b在同一媒质中沿x轴正方向传播，波速均为v＝2.5m/s。在t＝0时，两列波的波峰正好在x＝2.5m处重合，如图所示。t＝0时，两列波的波峰重合处的所有位置　　　　　　　

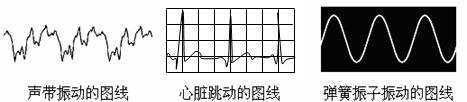
16、(4分)下图所示的三个图线分别是用不同的传感器测出的不同物体的振动图线。从三个图线可知，这三个物体振动的共同特点是具有　　　　　 。图中“心脏跳动的图线”是某人的心电图，若方格纸每个小方格的宽度是0.5cm，心电图记录仪拖动方格纸的速度是1.8cm/s，则此人的心率是每分钟　　　 次。

15、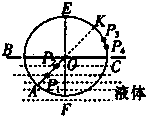(6分)学校开展研究性学习，某研究性学习小组的同学根据所学的光学知识，设计了一个测量液体折射率的仪器，如图所示．在一个圆形木盘上过其圆心O作两条相互垂直的直径BC、EF，在半径OA上垂直圆盘面插下两枚大头针P₁、P₂并保持P₁、P₂的位置不变，每次测量时，让圆盘的BFC部分竖直进入液体中，而且总使得液面与直径BC相平，EF为界面的法线，而后在图中右上方区域观察P₁、P₂的像，并在圆周上插上大头针P₃，使P₃正好挡住P₁、P₂．同学们通过计算，预先在圆周EC部分刻好了折射率的值。这样只要根据P所插的位置，就可直接读出液体折射率的值．则

　　 (1)若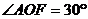，OP₃与OC的夹角为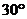，则P₃处所对应的折射率的值为________．

　　 (2)图中P₃、P₄两位置哪一处所对应的折射率值大？__________．

　　 (3)作AO的延长线交圆周于K，K处所对应的折射率的值应为_________．