
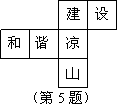
4.小红上学要经过三个十字路口,每个路口遇到红、绿灯的机会都相同,小红希望上学时经过每个路口都是绿灯,但实际这样的机会是( )
 A.
A.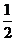 B.
B.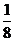 C.
C.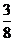 D.
D.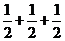
3.长度单位1纳米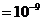 米,目前发现一种新型病毒直径为25100纳米,用科学记数法表示该病毒直径是( )
米,目前发现一种新型病毒直径为25100纳米,用科学记数法表示该病毒直径是( )
A.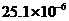 米 B.
米 B.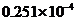 米
米
C.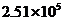 米 D.
米 D.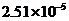 米
米
2.下列运算正确的是( )
A.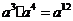 B.
B.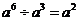
C.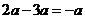 D.
D.
1.比1小2的数是( )
A.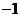 B.
B.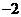 C.
C.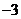 D.
D.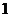
2. 概率与统计:
⑴随机变量的分布列:①随机变量分布列的性质:pi≥ 0, i=1,2,3,…; p1+p2+…=1;
②离散型随机变量:
|
X |
x1 |
X2 |
… |
X n |
… |
|
P |
P1 |
P2 |
… |
P n |
… |
均值(又称期望):EX= x1p1 + x2p2 + … + xn pn + … ;
方差:DX=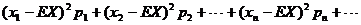 ;
;
注: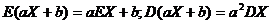 ;
;
③二项分布(独立重复试验):若X-B(n , p),则EX=n p, DX=n p(1- p) 注: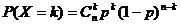 。
。
⑵条件概率:称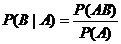 为在事件A发生的条件下,事件B发生的概率。注:0
为在事件A发生的条件下,事件B发生的概率。注:0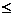 P(B|A)
P(B|A)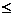 1
1
⑶独立事件同时发生的概率:P(AB)=P(A)P(B)。
⑷正态总体的概率密度函数: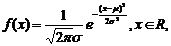 式中
式中 是参数,分别表示总体的平均数(期望值)EX与标准差
是参数,分别表示总体的平均数(期望值)EX与标准差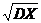
 ;
;
⑸正态曲线的性质:①曲线位于x轴上方,与x轴不相交;②曲线是单峰的,关于直线x=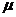 对称;③曲线在x=
对称;③曲线在x=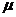 处达到峰值
处达到峰值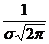 ;④曲线与x轴之间的面积为1;
;④曲线与x轴之间的面积为1;
①
当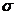 一定时,曲线随
一定时,曲线随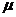 值的变化沿x轴平移;
值的变化沿x轴平移;
②
当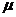 一定时,曲线形状由
一定时,曲线形状由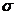 确定:
确定: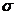 越大,曲线越“矮胖”,表示总体分布越分散;
越大,曲线越“矮胖”,表示总体分布越分散;
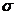 越小,曲线越“高瘦”,表示总体分布越集中。
越小,曲线越“高瘦”,表示总体分布越集中。
注:P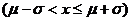 =0.6826;P
=0.6826;P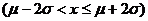 =0.9544
=0.9544
P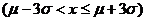 =0.9974
=0.9974
附:数学归纳法:一般的证明一个与正整数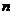 有关的一个命题,可按以下步骤进行:
有关的一个命题,可按以下步骤进行:
⑴证明当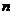 取第一个值
取第一个值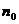 时命题成立;⑵假设当
时命题成立;⑵假设当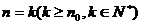 命题成立,证明当
命题成立,证明当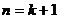 时命题也成立。那么由⑴⑵就可以判定命题对从
时命题也成立。那么由⑴⑵就可以判定命题对从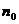 开始所有的正整数都成立。此证明方法叫数学归纳法。
开始所有的正整数都成立。此证明方法叫数学归纳法。
注:①数学归纳法的两个步骤缺一不可,用数学归纳法证明问题时必须严格按步骤进行;
②
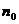 的取值视题目而定,可能是1,也可能是2等。
的取值视题目而定,可能是1,也可能是2等。
1. 排列、组合和二项式定理:
⑴排列数公式: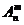 =n(n-1)(n-2)…(n-m+1)=
=n(n-1)(n-2)…(n-m+1)=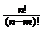 (m≤ n, m、n∈N*),
(m≤ n, m、n∈N*),
当m=n时为全排列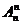 =n·(n-1)·(n-2)·…·3·2·1= n!
=n·(n-1)·(n-2)·…·3·2·1= n!
⑵组合数公式: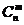 =
=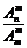 =
=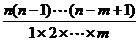 =
=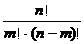 (
(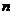 ,
,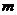 ∈N*,且
∈N*,且 )
)
⑶组合数性质: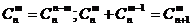
⑷二项式定理: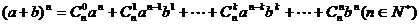
①通项: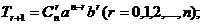 ②注意二项式系数与系数的区别
②注意二项式系数与系数的区别
⑸二项式系数的性质:(展开时有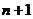 项)
项)
①与首末两端等距离的二项式系数相等;②若n为偶数,中间一项(第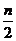 +1项)二项式系数最大;若n为奇数,中间两项(第
+1项)二项式系数最大;若n为奇数,中间两项(第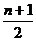 和
和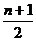 +1项)二项式系数最大;
+1项)二项式系数最大;
(6)求二项展开式各项系数和或奇(偶)数项系数和时,注意运用赋值法。
84.相互独立事件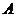 、
、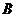 同时发生的概率:
同时发生的概率: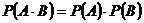 ;
;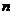 个相互独立事件同时发生的概率:
个相互独立事件同时发生的概率: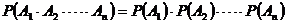 .
.
(上接第8页) 第十六部分 理科选修部分
83.①互斥事件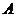 、
、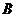 有一个发生的概率:
有一个发生的概率: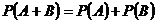 ;
;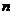 个互斥事件中有一个发生的概率:
个互斥事件中有一个发生的概率: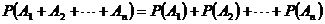 ;
;
②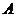 、
、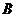 是两个任意事件,则
是两个任意事件,则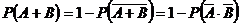 .
.
82.等可能性事件的概率: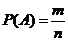 .(一次试验共有n个结果等可能的出现,事件A包含其中m个结果)
.(一次试验共有n个结果等可能的出现,事件A包含其中m个结果)
81.二项式定理: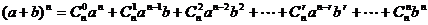 ;
;
二项展开式的通项公式: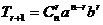
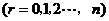 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com