
6.设f(x)=x3+x,则对任意实数a,b,“a+b≥0”是“f(a)+f(b)≥0”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
答案 C
5.(2008·山东文)设函数f(x)=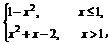 则f
则f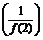 的值为
( )
的值为
( )
A.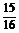 B.-
B.-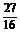 C.
C.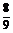 D.18
D.18
答案 A
4.如图所示,曲线是幂函数y=xn在第一象限的图象,已知n取±2、±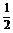 四个值,则相应的曲线C1,C2,C3,C4的n值依次为
( )
四个值,则相应的曲线C1,C2,C3,C4的n值依次为
( )
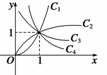 A.-2,-
A.-2,-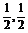 ,2
B.2,
,2
B.2,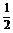 ,-
,-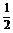 ,-2
,-2
C.-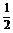 ,-2,2,
,-2,2,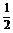 D.2,
D.2,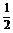 ,-2,-
,-2,-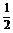
答案 B
3.如果幂函数y=(m2-3m+3)x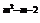 的图象不过原点,则m的取值是
( )
的图象不过原点,则m的取值是
( )
A.-1≤m≤2 B.m=1或m=2 C.m=2 D.m=1
答案 B
2.幂函数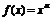 (
(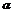 是有理数)的图象过点(2,
是有理数)的图象过点(2,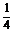 ),则f(x)的一个单调递减区间是
( )
),则f(x)的一个单调递减区间是
( )
A. B. (0,+∞)
C.
B. (0,+∞)
C.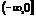 D. (-∞,0)
D. (-∞,0)
答案 B
1.设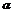 ∈{-1,1,
∈{-1,1,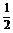 ,3},则使函数
,3},则使函数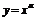 的定义域为R且为奇函数的所有的
的定义域为R且为奇函数的所有的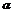 值为
( )
值为
( )
A. 1,3 B.-1,1 C.-1,3 D.-1,1,3
答案 A
3.幂函数y=x-1及直线y=x,y=1,x=1将平面直角坐标系的第一象限分成八个“卦限”:①、②、③、④、⑤、
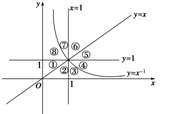 ⑥、⑦、⑧(如图所示),那么幂函数y=x
⑥、⑦、⑧(如图所示),那么幂函数y=x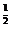 的图象经过的“卦限”是 ( )
的图象经过的“卦限”是 ( )
A.④⑦ B.④⑧
C.③⑧ D.①⑤
 答案?D?
答案?D?
2.已知幂函数y=x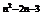 的图象与x、y轴都无公共点,且关于y轴对称,求整数n的值并画出该函数的草图.
的图象与x、y轴都无公共点,且关于y轴对称,求整数n的值并画出该函数的草图.
解 ∵函数图象与x、y轴都无公共点,
∴n2-2n-3≤0,∴-1≤n≤3.
又∵n为整数,∴n∈{-1,0,1,2,3}.
又图象关于y轴对称,∴n2-2n-3为偶数.
∴n=-1,1,3.
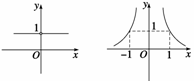 当n=-1和3时,n2-2n-3=0,y=x0图象如图(1)所示;
当n=-1和3时,n2-2n-3=0,y=x0图象如图(1)所示;
当n=1时,y=x-4,图象如图(2)所示. 图(1) 图(2)
1.已知函数f(x)=(m2+2m)·x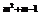 ,m为何值时,f(x)是
,m为何值时,f(x)是
(1)幂函数;
(2)正比例函数;
(3)反比例函数;
(4)二次函数.
解 (1)若f(x)为幂函数,则m2+2m=1,∴m=-1±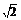 .
.
(2)若f(x)为正比例函数,则
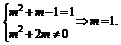
(3)若f(x)为反比例函数,则
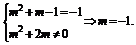
(4)若f(x)为二次函数,则
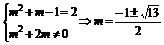 .
.
5.若(a+1)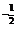 <(3-2a)
<(3-2a)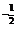 ,则a的取值范围是 .
,则a的取值范围是 .
答案 (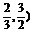

例1已知函数f(x)=(m2-m-1)x-5m-3,m为何值时,f(x):(1)是幂函数;(2)是幂函数,且是(0,+∞)上的增函数;
(3)是正比例函数;(4)是反比例函数;(5)是二次函数.
解 (1)因f(x)是幂函数,故m2-m-1=1,即m2-m-2=0,
解得m=2或m=-1.
(2)若f(x)是幂函数且又是(0,+∞)上的增函数,
则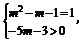 ∴m=-1.
∴m=-1.
(3)若f(x)是正比例函数,则-5m-3=1,解得m=-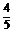 ,
,
此时m2-m-1≠0,故m=-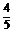 .
.
(4)若f(x)是反比例函数,则-5m-3=-1,
则m=-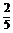 ,此时m2-m-1≠0,故m=-
,此时m2-m-1≠0,故m=-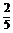 .
.
(5)若f(x)是二次函数,则-5m-3=2,即m=-1,此时m2-m-1≠0,故m=-1.
综上所述,当m=2或m=-1时,f(x)是幂函数;
当m=-1时,f(x)既是幂函数,又是(0,+∞)上的增函数;
当m=-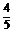 时,f(x)是正比例函数;
时,f(x)是正比例函数;
当m=-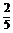 时,f(x)是反比例函数;
时,f(x)是反比例函数;
当m=-1时,f(x)是二次函数.
例2 点(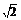 ,2)在幂函数f(x)的图象上,点(-2,
,2)在幂函数f(x)的图象上,点(-2,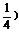 在幂函数g(x)的图象上,问当x为何值时,
在幂函数g(x)的图象上,问当x为何值时,
有f(x)>g(x),f(x)=g(x),f(x)<g(x).
解 设f(x)=xα,则由题意得2=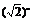 ,
,
∴α=2,即f(x)=x2,再设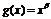 ,
,
则由题意得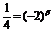 ,
,
∴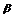 =-2,即g(x)=x-2,在同一坐标系中作出f(x)与g(x)的图象,如图所示.
=-2,即g(x)=x-2,在同一坐标系中作出f(x)与g(x)的图象,如图所示.
由图象可知:
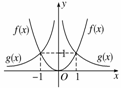 ①当x>1或x<-1时,
①当x>1或x<-1时,
f(x)>g(x);
②当x=±1时,f(x)=g(x);
③当-1<x<1且x≠0时,
f(x)<g(x).
例3 (12分) 已知幂函数f(x)=x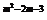 (m∈Z)为偶函数,且在区间(0,+∞)上是单调减函数.
(m∈Z)为偶函数,且在区间(0,+∞)上是单调减函数.
(1)求函数f(x);
(2)讨论F(x)=a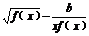 的奇偶性.
的奇偶性.
解 (1)∵f(x)是偶函数,∴m2-2m-3应为偶数. 2分
又∵f(x)在(0,+∞)上是单调减函数,
∴m2-2m-3<0,∴-1<m<3. 4分
又m∈Z,∴m=0,1,2.
当m=0或2时,m2-2m-3=-3不是偶数,舍去;
当m=1时,m2-2m-3=-4;
∴m=1,即f(x)=x-4. 6分
(2)F(x)= ,
,
∴F(-x)=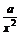 +bx3.
+bx3.
①当a≠0,且b≠0时,F(x)为非奇非偶函数;
②当a=0,b≠0时,F(x)为奇函数; 10分
③当a≠0,b=0时,F(x)为偶函数;
④当a=0,b=0时,F(x)既是奇函数,又是偶函数. 12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com