第一节 单项填空(共15小题；每小题l分，满分15分) 　　

　 从A、B、C、D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该选项的标号涂黑。

21．---Why not take _______ friend with you? Then you can share　 _______ cost of the car.

　　 ---That sounds like a good idea.

　　 A．a; a　　　　　 B．the; the　　　 C．a; the　　　　　 D．the; a

22．(14分) 在ΔABC中(如图1)，若CE是∠ACB的平分线，则＝.其证明过程：作EG⊥AC于点G，EH⊥BC于点H，CF⊥AB于点F

∵CE是∠ACB的平分线，

∴EG＝EH.

又∵＝＝，

＝＝，

∴＝.

(Ⅰ)把上面结论推广到空间中：在四面体A－BCD中(如图2)，平面CDE是二面角A－CD－B的角平分面，类比三角形中的结论，你得到的相应空间的结论是＿＿＿＿＿＿

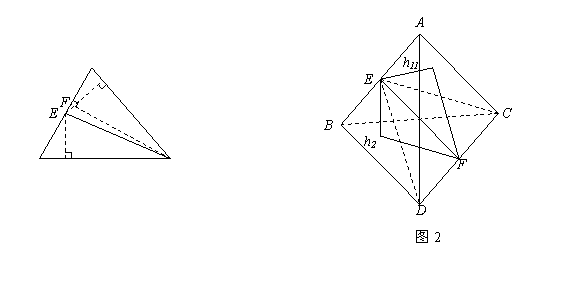(Ⅱ)证明你所得到的结论.

21．设事件A发生的概率为P，若在A发生的条件下B发生概率为P′，则由A产生B的概率为P·P′.根据这一事实解答下题.

一种掷硬币走跳棋的游戏：棋盘上有第0、1、2、…、100，共101站，一枚棋子开始在第0站(即P₀＝1)，由棋手每掷一次硬币，棋子向前跳动一次.若硬币出现正面则棋子向前跳动一站，出现反面则向前跳动两站.直到棋子跳到第99站(获胜)或第100站(失败)时，游戏结束.已知硬币出现正、反面的概率相同，设棋子跳到第到第n站时的概率为P_n.

(1)求P₁，P₂，P₃；

(2)设a_n=P_n－P_n－1(1≤n≤100)，求证：数列{a_n}是等比数列　 (12分)

20．用分析法证明：若a＞0，则－≥a+－2.(12分)

19．数列{a_n}的前n项和记为S_n，已知a₁＝1，a_n+1＝S_n(n＝1，2，3，…).

证明：⑴数列{}是等比数列；⑵S_n+1＝4a_n. (12分)

18．若a、b、c均为实数，且a＝x²－2x+，b＝y²－2y+，c＝z²－2z+，求证：a、b、c中至少有一个大于0. (12分)

16．(05黄冈市一模题)当a₀，a₁，a₂成等差数时，有a₀－2a₁+a₂＝0，当a₀，a₁，a₂，a₃成等差数列时，有a₀－3a₁+3a₂－a₃＝0，当a₀，a₁，a₂，a₃，a₄成等差数列时，有a₀－4a₁+6a₂－4a₃+a₄＝0，由此归纳：当a₀，a₁，a₂，…，a_n成等差数列时有C0na₀－C1na₁+C2na₂－…+Cnna_n＝0. 如果a₀，a₁，a₂，…，a_n成等差数列，类比上述方法归纳出的等式为＿＿＿。

三 解答题(74分)

17 已知△ABC中，角A、B、C成等差数列，求证：+=(12分)