
9.(2009·海淀模拟)若直线l1:y=k(x-4)与直线l2关于点(2,1)对称,则直线l2恒过定点( )
A.(0,4) B.(0,2) C.(-2,4) D.(4,-2)
解析:直线l1恒过定点(4,0),点(4,0)关于点(2,1)对称的点为(0,2),由题意知l2恒过点(0,2).
答案:B
8.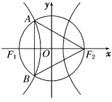 如右图,F1和F2分别是双曲线-=1(a>0,b>0)的
如右图,F1和F2分别是双曲线-=1(a>0,b>0)的
两个焦点,A和B是以O为圆心,以|OF1|为半径的圆
与该双曲线左支的两个交点,且△F2AB是等边三角形,
则双曲线的离心率为 ( )
A. B. C. D.1+
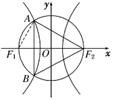 解析:连结AF1,则∠F1AF2=90°,∠AF2B=60°,
解析:连结AF1,则∠F1AF2=90°,∠AF2B=60°,
∴|AF1|=|F1F2|=c,
|AF2|=|F1F2|=c,
∴c-c=2a,∴e===1+.
答案:D
7.过点(0,1)的直线与x2+y2=4相交于A、B两点,则|AB|的最小值为 ( )
A.2 B.2 C.3 D.2
解析:当过点(0,1)的直线与直径垂直且(0,1)为垂足时,|AB|最小值为2.
答案:B
6.(2010·广州调研)已知点A(1,0),直线l:y=2x-4,点R是直线l上的一点,若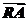 =
=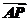 ,则点P的轨迹方程为 ( )
,则点P的轨迹方程为 ( )
 A.y=-2x
B.y=2x
C.y=2x-8 D.y=2x+4
A.y=-2x
B.y=2x
C.y=2x-8 D.y=2x+4
解析:设点P(x,y),R(x1,y1),∵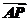 =
=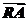 ,
,
∴(1-x1,-y1)=(x-1,y),
∴即
又点R在直线l上,∴-y=2(2-x)-4,
即2x-y=0为所求.
答案:B
5.直线2x-y-2=0绕它与y轴的交点逆时针旋转所得的直线方程是 ( )
A.-x+2y-4=0 B.x+2y-4=0
C.-x+2y+4=0 D.x+2y+4=0
解析:由题意知,两直线垂直,且已知直线过点(0,-2),所求直线斜率为-,∴所求直线方程为y+2=-x,即x+2y+4=0.
答案:D
4.(2010·厦门质检)直角坐标平面内过点P(2,1)且与圆x2+y2=4相切的直线 ( )
A.有两条 B.有且仅有一条
C.不存在 D.不能确定
解析:∵22+12>4,∴点P在圆外,故过点P与圆相切的直线有两条.
答案:A
3.若双曲线-y2=1的一个焦点为(2,0),则它的离心率为 ( )
A. B. C. D.2
解析:由题意知a2+1=4,∴a=,∴e===.
答案:C
2.(2010·苏州模拟)若ab<0,则过点P与Q的直线PQ的倾斜角的取值范围是 ( )
A. B. C. D.
解析:kPQ==,∵ab<0,∴<0,即k<0,
∴直线PQ的倾斜角的取值范围是.
答案:B
1.(2009·天津河西期末)点P(-2,1)到直线2x+y=5的距离为 ( )
A. B. C. D.
解析:点P到直线的距离d==.
答案:B
1 ?已知正方体
?已知正方体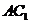 的棱长为
的棱长为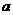 ,
,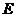 是
是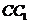 的中点,
的中点,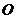 是对角线
是对角线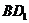 的中点,
的中点,
(1)求证: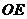 是异面直线
是异面直线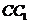 和
和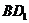 的公垂线;(2)求异面直线
的公垂线;(2)求异面直线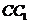 和
和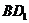 的距离
的距离
 解:(1)解法一:延长
解:(1)解法一:延长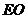 交
交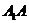 于
于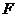 ,则
,则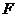 为
为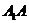 的中点,∴
的中点,∴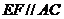 ,
,
∵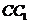
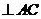 ,
,
∴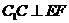 ,连结
,连结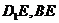 ,则
,则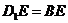 ,
,
又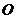 是
是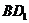 的中点,∴
的中点,∴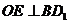 ,
,
 ∴
∴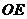 是异面直线
是异面直线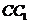 和
和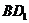 的公垂线
的公垂线
(2)由(1)知,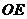
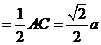 .
.
解法二:建立空间直角坐标系,用坐标运算证明(略)
引申:求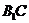 与
与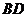 间的距离
间的距离
解法一:(转化为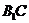 到过
到过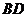 且与
且与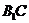 平行的平面的距离)
平行的平面的距离)
连结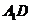 ,则
,则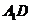 //
//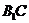 ,∴
,∴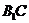 //平面
//平面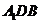 ,连
,连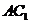 ,可证得
,可证得
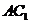
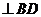 ,
,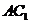
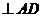 ,∴
,∴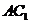
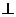 平面
平面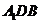 ,
,
∴平面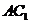
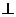 平面
平面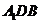 ,且两平面的交线为
,且两平面的交线为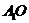 ,过
,过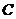 作
作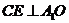 ,垂足为
,垂足为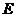 ,则
,则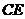 即为
即为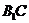 与平面
与平面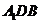 的距离,也即
的距离,也即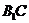 与
与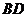 间的距离,
间的距离,
在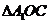 中,
中,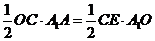 ,∴
,∴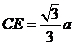 .
.
(解法二):坐标法:
以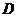 为原点,
为原点,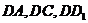 所在的直线分别为
所在的直线分别为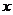 轴,
轴,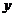 轴、
轴、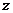 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则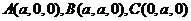 ,
,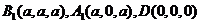 ,
,
由(解法一)求点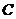 到平面
到平面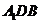 的距离
的距离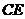 ,设
,设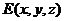 ,
,
∵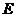 在平面
在平面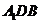 上,
上,
∴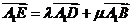 ,即
,即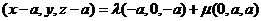 ,
,
∴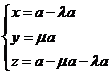 ,
,
∵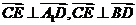 ,∴
,∴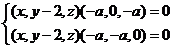 ,
,
解得: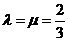 ,∴
,∴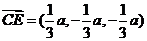 ,∴
,∴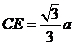 .
.
解法三:直接求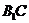 与
与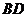 间的距离
间的距离
设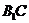 与
与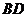 的公垂线为
的公垂线为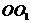 ,且
,且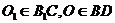 ,
,
设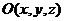 ,设
,设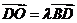 ,
,
则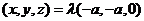 ,∴
,∴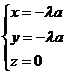 ,∴
,∴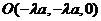 ,
,
同理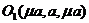 ,
,
∴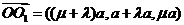 ,∴
,∴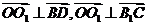 ,
,
∴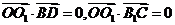 ,
,
解得: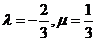 ,
,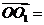
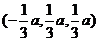 ,
,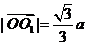 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com