
6.a、b∈R,且|a|<1,|b|<1,则无穷数列:1,(1+b)a,(1+b+b2)a2,…,1+b+b2+…+bn-1)an-1…的和为 ( )
A.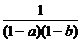 B.
B.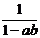
C.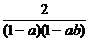 D.
D.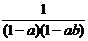
5.已知等差数列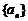 中,
中,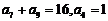 ,则
,则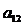 的值是 ( )
的值是 ( )
A.15 B.30 C.31 D.64
4.如果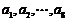 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差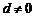 ,则 ( )
,则 ( )
A.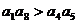 B.
B.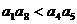
C.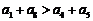 D.
D.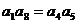
3.在等差数列中,前n项的和为Sn,若Sm=2n,Sn=2m,(m、n∈N且m≠n),则公差d的值为( )
A.-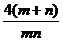 B.-
B.-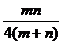
C.-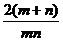 D.-
D.-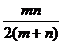
2.已知数列{an}中,an=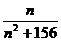 (n∈N),则数列{an}的最大项是 ( )
(n∈N),则数列{an}的最大项是 ( )
A.第12项 B.第13项
C.第12项或13项 D.不存在
1.“公差为0的等差数列是等比数列”;“公比为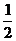 的等比数列一定是递减数列”;“a,b,c三数成等比数列的充要条件是b2= ac”;“a,b,c三数成等差数列的充要条件是2b= a+c”,以上四个命题中,正确的有 ( )
的等比数列一定是递减数列”;“a,b,c三数成等比数列的充要条件是b2= ac”;“a,b,c三数成等差数列的充要条件是2b= a+c”,以上四个命题中,正确的有 ( )
A.1个 B.2个 C.3个 D.4个
22.(14分)已知椭圆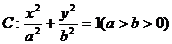 的离心率为
的离心率为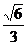 ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且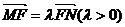 ,定点A(-4,0).
,定点A(-4,0).
(I)求证:当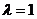 时
时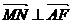 ;
;
(II)若当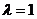 时有
时有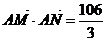 ,求椭圆C的方程;
,求椭圆C的方程;
(III)在(2)的条件下,当M、N两点在椭圆C运动时,试判断 是否有最大值,若存在求出最大值,并求出这时M、N两点所在直线方程,若不存在,给出理由.
是否有最大值,若存在求出最大值,并求出这时M、N两点所在直线方程,若不存在,给出理由.
21.(12分)已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
(I)求动圆圆心的轨迹M的方程;
(II)设过点P,且斜率为-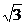 的直线与曲线M相交于A、B两点.
的直线与曲线M相交于A、B两点.
(i)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
(ii)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
20.(12分)设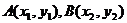 两点在抛物线
两点在抛物线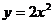 上,
上,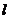 是AB的垂直平分线,
是AB的垂直平分线,
(I)当且仅当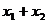 取何值时,直线
取何值时,直线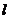 经过抛物线的焦点F?证明你的结论;
经过抛物线的焦点F?证明你的结论;
(II)当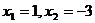 时,求直线
时,求直线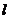 的方程.
的方程.
19.(12分)已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1,动点M到圆C的切线长与|MQ|的比等于常数λ(λ>0).求动点M的轨迹方程,说明它表示什么曲线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com