
19.(12分)设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC=
∠DBC=120°. 求:
(I)直线AD与平面BCD所成角的大小;
(II)异面直线AD与BC所成的角的大小;
(III)二面角A-BD-C的平面角正切值大小.
18.(12分)平面EFGH分别平行空间四边形ABCD中的CD与AB且交BD、AD、AC、BC于E、F、G、H.CD=a,AB=b,CD⊥AB.
(I)求证EFGH为矩形;
(II)点E在什么位置,SEFGH最大?
17.(12分)在平面α内有△ABC,在平面α外有点S,斜线SA⊥AC,SB⊥BC,且斜线SA、SB与平面α所成角相等.
(I)求证:AC=BC;
(II)又设点S到α的距离为4cm,AC⊥BC且AB=6cm,求S与AB的距离.
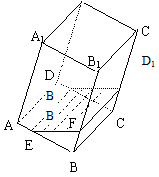
16.如图,在透明材料制成的长方体容器ABCD-A1B1C1D1内灌注
一些水,固定容器底面一边BC于桌面上,再将容器倾斜根据
倾斜度的不同,有下列命题:
(1)水的部分始终呈棱柱形;
(2)水面四边形EFGH的面积不会改变;
(3)棱A1D1始终与水面EFGH平行;
(4)当容器倾斜如图所示时,BE·BF是定值。
其中所有正确命题的序号是 .
15.多面体上位于同一条棱两端的顶点称为相邻的,如图,
正方体的一个顶点A在平面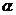 内,其余顶点在
内,其余顶点在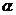 的
的
同侧,正方体上与顶点A相邻的三个顶点到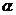 的距
的距
离分别为1,2和4,P是正方体的其余四个顶点中的
一个,则P到平面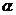 的距离可能是:
的距离可能是:
①3; ②4; ③5; ④6; ⑤7
以上结论正确的为______________.
 (写出所有正确结论的编号)
(写出所有正确结论的编号)
14.如图,矩形ABCD中,DC=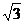 ,AD=1,在DC上截取DE=1,
,AD=1,在DC上截取DE=1,
将△ADE沿AE翻折到D1点,点D1在平面ABC上的射影落
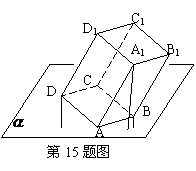 在AC上时,二面角D1-AE-B的平面角的余弦值
在AC上时,二面角D1-AE-B的平面角的余弦值
是 .
13. 某地球仪上北纬
某地球仪上北纬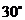 纬线的长度为
纬线的长度为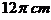 ,该地球仪的半径是__________cm,表面积是______________cm2.
,该地球仪的半径是__________cm,表面积是______________cm2.
12.将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为 ( )
A.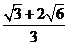 B.2+
B.2+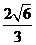 C.4+
C.4+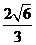 D.
D.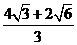
第Ⅱ卷
11.底面边长为a,高为h的正三棱锥内接一个正四棱柱(此时正四棱柱上底面有两个顶点在同一个侧面内),此棱柱体积的最大值 ( )
A.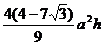 B.
B.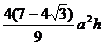
C.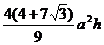 D.
D.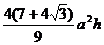
10.在半径为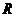 的球内有一内接正三棱锥,它的底面三个顶点恰好
的球内有一内接正三棱锥,它的底面三个顶点恰好
都在同一个大圆上,一个动点从三棱锥的一个顶点出发沿球面
运动,经过其余三点后返回,则经过的最短路程是( )
A.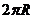 B.
B.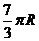 C.
C.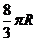 D.
D.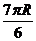
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com