
2.若函数f(x)的定义域是[0,1],则f(x+a)·f(x-a)(0<a< )的定义域是
( )
)的定义域是
( )
?A.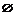 ?
B.[a,1-a]
C.[-a,1+a]?
D.[0,1]
?
B.[a,1-a]
C.[-a,1+a]?
D.[0,1]
答案?B
1.求下列函数的定义域:
(1)y=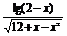 +(x-1)0
;
(2)y=
+(x-1)0
;
(2)y=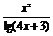 +(5x-4)0;
+(5x-4)0;
(3)y=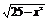 +lgcosx;
(4)y=lg(ax-k·2x) (a>0).
+lgcosx;
(4)y=lg(ax-k·2x) (a>0).
解 (1)由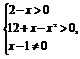 得
得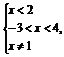
所以-3<x<2且x≠1.
故所求函数的定义域为(-3,1)∪(1,2).
(2)由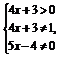 得
得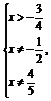
∴函数的定义域为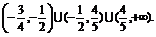
(3)由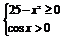 ,得
,得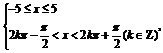
借助于数轴,解这个不等式组,得函数的定义域为
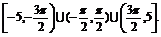
(4)由ax-k·2x>0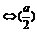 x>k (a>0).若k≤0,∵(
x>k (a>0).若k≤0,∵(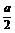 )x>0,∴x∈R.
)x>0,∴x∈R.
若k>0,则当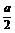 >1,即a>2时,
>1,即a>2时,
函数的定义域为{x|x>log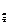 k};
k};
当0<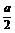 <1,即0<a<2时,
<1,即0<a<2时,
函数的定义域为{x|x<log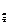 k};
k};
当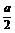 =1,即a=2时,
=1,即a=2时,
则有1x>k,若0<k<1,则函数的定义域为R;
若k≥1,则x∈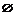 ,即原式无意义.
,即原式无意义.
5.若函数y=x2-3x-4的定义域为[0,m],值域为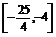 ,则m的取值范围是
( )
,则m的取值范围是
( )
?A.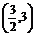 ? B.
? B. ? C.(0,3]?
D.
? C.(0,3]?
D.
答案?B?

例1求下列函数的定义域:
(1)y=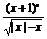 ;
;
(2)y=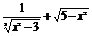 ;
;
(3)y=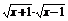 .
.
解 (1)由题意得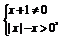 化简得
化简得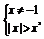
即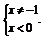 故函数的定义域为{x|x<0且x≠-1}.
故函数的定义域为{x|x<0且x≠-1}.
(2)由题意可得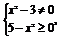 解得
解得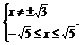
故函数的定义域为{x|-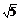 ≤x≤
≤x≤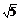 且x≠±
且x≠±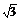 }.
}.
(3)要使函数有意义,必须有
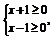 即
即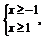 ∴x≥1,故函数的定义域为[1,+∞).
∴x≥1,故函数的定义域为[1,+∞).
例2 设函数y=f(x)的定义域为[0,1],求下列函数的定义域.
(1)y=f(3x); (2)y=f(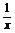 );
);
(3)y=f(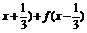 ;
;
(4)y=f(x+a)+f(x-a).
解 (1)0≤3x≤1,故0≤x≤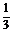 ,
,
y=f(3x)的定义域为[0, 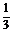 ].
].
(2)仿(1)解得定义域为[1,+∞).
(3)由条件,y的定义域是f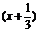 与
与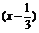 定义域的交集.
定义域的交集.
列出不等式组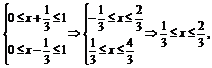
故y=f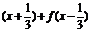 的定义域为
的定义域为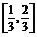 .
.
(4)由条件得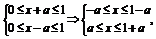 讨论:
讨论:
①当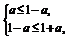 即0≤a≤
即0≤a≤ 时,定义域为[a,1-a];
时,定义域为[a,1-a];
②当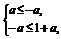 即-
即- ≤a≤0时,定义域为[-a,1+a].
≤a≤0时,定义域为[-a,1+a].
综上所述:当0≤a≤ 时,定义域为[a,1-a];
时,定义域为[a,1-a];
当- ≤a≤0时,定义域为[-a,1+a].
≤a≤0时,定义域为[-a,1+a].
例3 求下列函数的值域:
(1)y=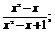 (2)y=x-
(2)y=x-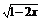 ;
;
(3)y=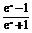 .
.
解 (1)方法一 (配方法)
∵y=1-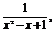 而
而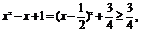
∴0<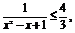 ∴
∴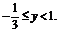 ∴值域为
∴值域为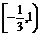 .
.
方法二 (判别式法)
由y=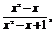 得(y-1)
得(y-1)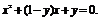
∵y=1时,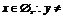 1.又∵
1.又∵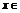 R,∴必须
R,∴必须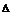 =(1-y)2-4y(y-1)≥0.
=(1-y)2-4y(y-1)≥0.
∴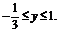 ∵
∵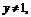 ∴函数的值域为
∴函数的值域为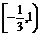 .22222222
.22222222
(2)方法一 (单调性法)
定义域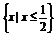 ,函数y=x,y=-
,函数y=x,y=-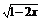 均在
均在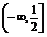 上递增,故y≤
上递增,故y≤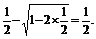
∴函数的值域为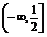 .
.
方法二 (换元法)
令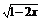 =t,则t≥0,且x=
=t,则t≥0,且x=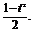
∴y=- (t+1)2+1≤
(t+1)2+1≤ (t≥0),
(t≥0),
∴y∈(-∞, ].
].
(3)由y=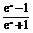 得,ex=
得,ex=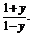
∵ex>0,即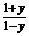 >0,解得-1<y<1.
>0,解得-1<y<1.
∴函数的值域为{y|-1<y<1}.
例4(12分)若函数f(x)= x2-x+a的定义域和值域均为[1,b](b>1),求a、b的值.
x2-x+a的定义域和值域均为[1,b](b>1),求a、b的值.
解 ∵f(x)= (x-1)2+a-
(x-1)2+a- .
2分
.
2分
∴其对称轴为x=1,即[1,b]为f(x)的单调递增区间. 4分
∴f(x)min=f(1)=a- =1
① 6分
=1
① 6分
f(x)max=f(b)= b2-b+a=b
② 8分
b2-b+a=b
② 8分
由①②解得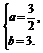 12分
12分

4.函数y=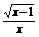 的值域是
( )
的值域是
( )
?A.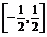 B.
B. ?
C.[0,1]?
D.[0,+∞)
?
C.[0,1]?
D.[0,+∞)
答案?B?
2.若函数f(x)=loga(x+1)(a>0且a≠1)的定义域和值域都是[0,1],则a等于 ( )
?A.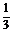 ?
B.
?
B.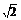 C.
C.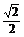 ?
D.2
?
D.2
答案?D?
2.函数f(x)=3x(0<x≤2)的反函数的定义域为 ( )
?A.(0,+∞) B.(1,9]? C.(0,1)? D.[9,+∞)
答案?B?
1.(2008·全国Ⅰ理,1)函数y=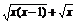 的定义域为
(
)
的定义域为
(
)
?A.{x|x≥0}? B.{x|x≥1}
?C.{x|x≥1}∪{0}? D.{x|0≤x≤1}
答案 C?
12.某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3 600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解 (1)当每辆车的月租金定为3 600元时,未租出的车辆数为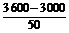 =12,所以这时租出了88辆车.
=12,所以这时租出了88辆车.
(2)设每辆车的月租金定为x元,则租赁公司的月收益为f(x)=(100-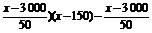 ×50
×50
整理得f(x)=-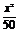 +162x-21 000=-
+162x-21 000=-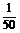 (x-4 050)2+307 050.
(x-4 050)2+307 050.
所以,当x=4 050时,f(x)最大,最大值为f(4 050)=307 050.
即当每辆车的月租金定为4 050元时,租赁公司的月收益最大,最大月收益为307 050元.
§2.2 函数的定义域、值域
 22xc2
22xc2
 基础自测
基础自测
11.如图所示,有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,且上底CD的端点在圆周上,写出梯形周长y关于腰长x的函数关系式,并求出它的定义域.
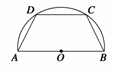 解 AB=2R,C、D在⊙O的半圆周上,
解 AB=2R,C、D在⊙O的半圆周上,
设腰长AD=BC=x,作DE⊥AB,
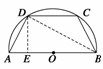 垂足为E,连接BD,
垂足为E,连接BD,
那么∠ADB是直角,
由此Rt△ADE∽Rt△ABD.
∴AD2=AE×AB,即AE=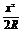 ,∴CD=AB-2AE=2R-
,∴CD=AB-2AE=2R-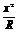 ,
,
所以y=2R+2x+(2R-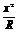 ), 即y=-
), 即y=-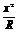 +2x+4R.
+2x+4R.
再由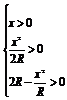 ,解得0<x<
,解得0<x<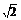 R.所以y=-
R.所以y=-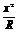 +2x+4R,定义域为(0,
+2x+4R,定义域为(0,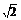 R).
R).
10.已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(1)求g(x)的解析式;
(2)解不等式g(x)≥f(x)-|x-1|.
解 (1)设函数y=f(x)的图象上任一点Q(x0,y0)关于原点的对称点为P(x,y),
则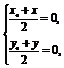 即
即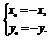
∵点Q(x0,y0)在函数y=f(x)的图象上∴-y=x2-2x,即y=-x2+2x,故g(x)=-x2+2x.
(2)由g(x)≥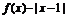 可得:2x2-|x-1|≤0.
可得:2x2-|x-1|≤0.
当x≥1时,2x2-x+1≤0,此时不等式无解.
当x<1时,2x2+x-1≤0,∴-1≤x≤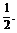 因此,原不等式的解集为
因此,原不等式的解集为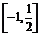 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com