
3、关于地球上生命物质存在的基本条件的叙述,不正确的是
A.充足的水分 B.恰到好处的大气厚度和大气成分
C.适宜的太阳光照和温度范围 D.地球常遭小行星撞击
2、关于太阳活动的正确说法是:
A、耀斑是太阳活动的主要标志 B、黑子出现是太阳活动的激烈显示
C、太阳黑子活动频繁时,耀斑活动也增强 D、黑子的活动周期大约为8年
1、下列现象与地球自转有关的是
A.昼夜的产生 B.昼夜交替 C.昼夜长短的变化 D.极昼和极夜
2. 概率与统计
⑴随机变量的分布列:
①随机变量分布列的性质:pi≥0,i=1,2,…; p1+p2+…=1;
②离散型随机变量:
|
X |
x1 |
X2 |
… |
xn |
… |
|
P |
P1 |
P2 |
… |
Pn |
… |
期望:EX= x1p1 + x2p2 + … + xnpn + … ;
方差:DX=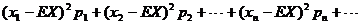 ;
;
注: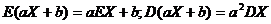 ;
;





|
 X 0 1 期望:EX=p;方差:DX=p(1-p).
X 0 1 期望:EX=p;方差:DX=p(1-p).
P 1-p p

① 超几何分布:
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则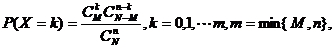 其中,
其中,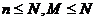 。
。
称分布列

X 0 1 … m
 P
P 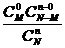
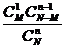 …
… 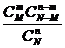
 为超几何分布列, 称X服从超几何分布。
为超几何分布列, 称X服从超几何分布。
⑤二项分布(独立重复试验):
若X-B(n,p),则EX=np,
DX=np(1-
p);注: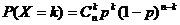 。
。
⑵条件概率:称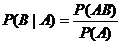 为在事件A发生的条件下,事件B发生的概率。
为在事件A发生的条件下,事件B发生的概率。
注:①0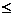 P(B|A)
P(B|A)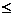 1;②P(B∪C|A)=P(B|A)+P(C|A)。
1;②P(B∪C|A)=P(B|A)+P(C|A)。
⑶独立事件同时发生的概率:P(AB)=P(A)P(B)。
⑷正态总体的概率密度函数: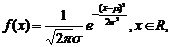 式中
式中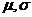 是参数,分别表示总体的平均数(期望值)与标准差;
是参数,分别表示总体的平均数(期望值)与标准差;
(6)正态曲线的性质:
①曲线位于x轴上方,与x轴不相交;②曲线是单峰的,关于直线x=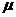 对称;
对称;
③曲线在x=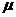 处达到峰值
处达到峰值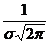 ;④曲线与x轴之间的面积为1;
;④曲线与x轴之间的面积为1;
②
当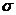 一定时,曲线随
一定时,曲线随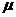 质的变化沿x轴平移;
质的变化沿x轴平移;
③
当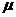 一定时,曲线形状由
一定时,曲线形状由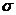 确定:
确定: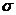 越大,曲线越“矮胖”,表示总体分布越集中;
越大,曲线越“矮胖”,表示总体分布越集中;
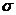 越小,曲线越“高瘦”,表示总体分布越分散。
越小,曲线越“高瘦”,表示总体分布越分散。
注:P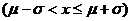 =0.6826;P
=0.6826;P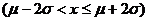 =0.9544
=0.9544
P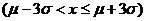 =0.9974
=0.9974
1. 排列、组合和二项式定理
⑴排列数公式: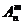 =n(n-1)(n-2)…(n-m+1)=
=n(n-1)(n-2)…(n-m+1)=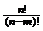 (m≤n,m、n∈N*),当m=n时为全排列
(m≤n,m、n∈N*),当m=n时为全排列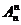 =n(n-1)(n-2)…3.2.1=n!;
=n(n-1)(n-2)…3.2.1=n!;
⑵组合数公式: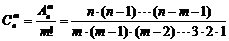 (m≤n),
(m≤n),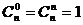 ;
;
⑶组合数性质: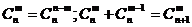 ;
;
⑷二项式定理: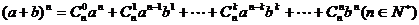
①通项: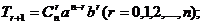 ②注意二项式系数与系数的区别;
②注意二项式系数与系数的区别;
⑸二项式系数的性质:
①与首末两端等距离的二项式系数相等;②若n为偶数,中间一项(第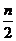 +1项)二项式系数最大;若n为奇数,中间两项(第
+1项)二项式系数最大;若n为奇数,中间两项(第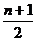 和
和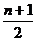 +1项)二项式系数最大;
+1项)二项式系数最大;
③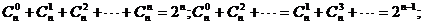
(6)求二项展开式各项系数和或奇(偶)数项系数和时,注意运用赋值法。
⑴综合法
一般地,利用已知条件和某些数学定义、定理、公理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法。综合法又叫顺推法或由因导果法。
⑵分析法
一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、定理、公理等),这种证明的方法叫分析法。分析法又叫逆推证法或执果索因法。
2.间接证明------反证法
一般地,假设原命题不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立,这种证明方法叫反证法。
附:数学归纳法(仅限理科)
一般的证明一个与正整数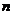 有关的一个命题,可按以下步骤进行:
有关的一个命题,可按以下步骤进行:
⑴证明当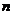 取第一个值
取第一个值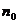 是命题成立;
是命题成立;
⑵假设当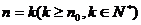 命题成立,证明当
命题成立,证明当 时命题也成立。
时命题也成立。
那么由⑴⑵就可以判定命题对从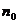 开始所有的正整数都成立。
开始所有的正整数都成立。
注:①数学归纳法的两个步骤缺一不可,用数学归纳法证明问题时必须严格按步骤进行;
②
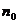 的取值视题目而定,可能是1,也可能是2等。
的取值视题目而定,可能是1,也可能是2等。
1.推理:
⑴合情推理:归纳推理和类比推理都是根据已有事实,经过观察、分析、比较、联想,在进行归纳、类比,然后提出猜想的推理,我们把它们称为合情推理。
①归纳推理:由某类食物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者有个别事实概括出一般结论的推理,称为归纳推理,简称归纳。
注:归纳推理是由部分到整体,由个别到一般的推理。
②类比推理:由两类对象具有类似和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,称为类比推理,简称类比。
注:类比推理是特殊到特殊的推理。
⑵演绎推理:从一般的原理出发,推出某个特殊情况下的结论,这种推理叫演绎推理。
注:演绎推理是由一般到特殊的推理。
“三段论”是演绎推理的一般模式,包括:⑴大前提---------已知的一般结论;⑵小前提---------所研究的特殊情况;⑶结 论---------根据一般原理,对特殊情况得出的判断。
4. 全称量词与存在量词
全称量词与存在量词
⑴全称量词-------“所有的”、“任意一个”等,用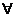 表示;
表示;
全称命题p: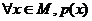 ; 全称命题p的否定
; 全称命题p的否定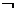 p:
p: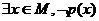 。
。
⑵存在量词--------“存在一个”、“至少有一个”等,用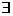 表示;
表示;
特称命题p: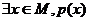 ; 特称命题p的否定
; 特称命题p的否定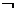 p:
p: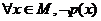 ;
;
3.逻辑连接词:






 ⑴且(and) :命题形式
p
⑴且(and) :命题形式
p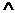 q;
p q p
q;
p q p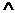 q p
q p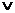 q
q 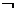 p
p
 ⑵或(or):命题形式 p
⑵或(or):命题形式 p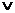 q; 真 真 真 真 假
q; 真 真 真 真 假
 ⑶非(not):命题形式
⑶非(not):命题形式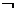 p .
真 假 假 真 假
p .
真 假 假 真 假
 假 真 假 真 真
假 真 假 真 真
 假 假 假 假 真
假 假 假 假 真
2.充要条件的判断:
(1)定义法----正、反方向推理;
(2)利用集合间的包含关系:例如:若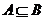 ,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;
,则A是B的充分条件或B是A的必要条件;若A=B,则A是B的充要条件;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com