
2.已知圆的方程为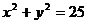 ,求过圆上一点
,求过圆上一点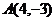 的切线方程.
的切线方程.
[学生活动]探究方法
 [教师预设]
[教师预设]
方法一:待定系数法(利用几何关系求斜率-垂直)
方法二:待定系数法(利用代数关系求斜率-联立方程)
方法三:轨迹法(利用勾股定理列关系式) [多媒体课件演示]
方法四:轨迹法(利用向量垂直列关系式)
I.直接应用(内化新知)
问题三:1.写出下列各圆的方程(课本P77练习1)
(1)圆心在原点,半径为3;
(2)圆心在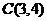 ,半径为
,半径为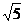 ;
;
(3)经过点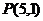 ,圆心在点
,圆心在点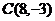 .
.
2.根据圆的方程写出圆心和半径
(1)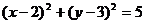 ; (2)
; (2)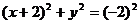 .
.
II.灵活应用(提升能力)
问题四:1.求以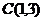 为圆心,并且和直线
为圆心,并且和直线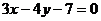 相切的圆的方程.
相切的圆的方程.
[教师引导]由问题三知:圆心与半径可以确定圆.
 问题一:已知隧道的截面是半径为4m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7m,高为3m的货车能不能驶入这个隧道?
问题一:已知隧道的截面是半径为4m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7m,高为3m的货车能不能驶入这个隧道?
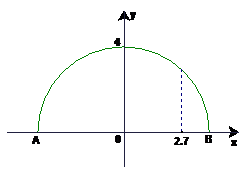
[引导] 画图建系
[学生活动]:尝试写出曲线的方程(对求曲线的方程的步骤及圆的定义进行提示性复习)
解:以某一截面半圆的圆心为坐标原点,半圆的直径AB所在直线为x轴,建立直角坐标系,则半圆的方程为x2+y2=16(y≥0)
将x=2.7代入,得 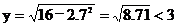 .
.
即在离隧道中心线2.7m处,隧道的高度低于货车的高度,因此货车不能驶入这个隧道。
 (二)深入探究(获得新知)
(二)深入探究(获得新知)
问题二:1.根据问题一的探究能不能得到圆心在原点,半径为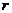 的圆的方程?
的圆的方程?
答:x2+y2=r2
2.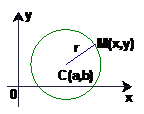 如果圆心在
如果圆心在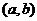 ,半径为
,半径为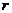 时又如何呢?
时又如何呢?
[学生活动] 探究圆的方程。
[教师预设] 方法一:坐标法
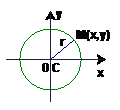
如图,设M(x,y)是圆上任意一点,根据定义点M到圆心C的距离等于r,所以圆C就是集合P={M||MC|=r}
由两点间的距离公式,点M适合的条件可表示为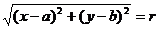 ①
①
把①式两边平方,得(x―a)2+(y―b)2=r2
方法二:图形变换法
方法三:向量平移法
13、已知四面体各棱长是1或2,且该四面体不是正四面体,求这个四面体体积的所有可能的值。
12、(05福建)如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
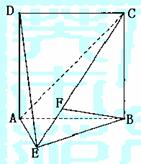 (Ⅰ)求证AE⊥平面BCE;
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离.
11、 (05全国卷1) 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
(05全国卷1) 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,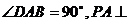 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=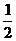 AB=1,M是PB的中点。
AB=1,M是PB的中点。
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小。
10、已知正三棱柱ABC-A1B1C1的底面边长为2cm, 高为4cm,过BC作一个截面,截面与底面ABC成60°角,则截面的面积是
7、正四棱锥S-ABCD的侧棱长为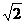 ,底面的边长为
,底面的边长为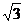 ,E是SA的中点,则异面直线BE与SC所成的角为
。
8、已知a=(3,1,5), b=(1,2,-3), 向量c与z轴垂直,且满足c×a=9, c×b=-4,则c=
9、已知PA、PB、PC两两垂直且PA=
,E是SA的中点,则异面直线BE与SC所成的角为
。
8、已知a=(3,1,5), b=(1,2,-3), 向量c与z轴垂直,且满足c×a=9, c×b=-4,则c=
9、已知PA、PB、PC两两垂直且PA=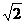 ,PB=
,PB=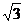 ,PC=2,则过P、A、B、C四点的球的体积为
。
,PC=2,则过P、A、B、C四点的球的体积为
。
7.某县位于沙漠地带,人与自然长期进行着顽强的斗争,到2001年底全县的绿化率已达30%。从2002年开始,每年将出现这样的局面,即原有沙漠面积的16%将被绿化,与此同时,由于各种原因,原有绿化面积的4%又被沙化。
(1)设全县面积为1,2001年底绿化面积为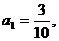 经过
经过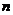 年绿化总面积为
年绿化总面积为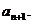
求证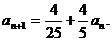
(2)至少需要多少年(年取整数,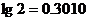 )的努力,才能使全县的绿化率达到60%?
)的努力,才能使全县的绿化率达到60%?
6.数列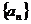 的前
的前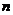 项和
项和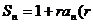 为不等于0,1的常数),求其通项公式
为不等于0,1的常数),求其通项公式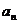
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com