
答案:1.⑴真;⑵真;⑶假.
2.⑴p或q:4∈{2,3}或2∈{2,3};p且q:4∈{2,3}且2∈{2,3};非p:4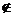 {2,3}.
{2,3}.
∵p假q真,∴“p或q”为真,“p且q”为假,“非p”为真.
⑵p或q:2是偶数或不是质数;p且q:2是偶数且不是质数;非p:2不是偶数.
∵p真q假,∴“p或q”为真,“p且q”为假,“非p”为假.
5.学习逻辑的意义
一方面是因为数学基础需要用逻辑来阐明,另一方面是因为计算机离不开数学逻辑,课本中介绍的洗衣机上的“或门电路”和电子保险门上的“与门电路”就是两个在这方面应用的实例.可以说计算机的“智能”装置是以数学逻辑为基础进行设计的.
同学们可以结合日常生活中电器的自动控制功能,再找出一些这样的例子.
电路:

或门电路(或) 与门电路(且)
4.逻辑符号
“或”的符号是“∨”,“且”的符号是“∧”,“非”的符号是“┐”.
例如,“p或q”可记作“p∨q”; “p且q”可记作“p∧q”;“非p”可记作“┐p”.
注意:数学中的“或”与日常生活用语中的“或”的区别
“或”这个逻辑联结词的用法,一般有两种解释:
一是“不可兼有”,即“a或b”是指a,b中的某一个,但不是两者.日常生活中有时采用这一解释.例如“你去或我去”,人们在理解上不会认为有你我都去这种可能.
二是“可兼有”,即“a或b”是指a,b中的任何一个或两者.例如“x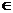 A或x
A或x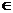 B”,是指x可能属于A但不属于B(这里的“但”等价于“且”),x也可能不属于A但属于B,x还可能既属于A又属于B(即x
B”,是指x可能属于A但不属于B(这里的“但”等价于“且”),x也可能不属于A但属于B,x还可能既属于A又属于B(即x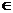 A∩B);又如在“p真或q真”中,可能只有p真,也可能只有q真,还可能p,q都为真.数学书中一般采用这种解释,运用数学语言和解数学题时,都要遵守这一点.还要注意“可兼有”并不意味“一定兼有”.
A∩B);又如在“p真或q真”中,可能只有p真,也可能只有q真,还可能p,q都为真.数学书中一般采用这种解释,运用数学语言和解数学题时,都要遵守这一点.还要注意“可兼有”并不意味“一定兼有”.
另外,“苹果是长在树上或长在地里”这一命题,按真值表判断,它是真命题,但在日常生活中,我们认为这句话是不妥的.
3.“p或q”形式的复合命题:
例3.如果p表示“5是12的约数” q表示“5是15的约数”,r表示“5是8的约数”,写出,p或r,q或s,p或q的复合命题,并判断其真假,归纳其规律.
p或q即“5是12的约数或是15的约数”为真(p为假、q为真);
p或r即“5是12的约数或是8的约数”为假(p、r为假)
小结:“p或q”形式的复合命题真假判断
当p,q中至少有一个为真时,“p或q”为真;当p,q都为假时,“p或q”为假. 即“p或q”形式的复合命题,当p与q同为假时为假,其他情况时为真. 可用下表表示.
|
p |
q |
p或q |
|
真 |
真 |
真 |
|
真 |
假 |
真 |
|
假 |
真 |
真 |
|
假 |
假 |
假 |
像上面三个表用来表示命题的真假的表叫做真值表.
在真值表中,是根据简单命题的真假,判断由这些简单命题构成的复合命题的真假,而不涉及简单命题的具体内容.
例4(课本第28页例2)分别指出由下列各组命题构成的“ p或q”,“p且q”,“非p”形式的复合命题的真假:
① p:2+2=5,q:3>2;
② p:9是质数,q:8是12的约数;
③ p:1∈{1,2},q:{1}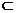 {1,2};
{1,2};
④ p:φ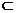 {0},q:φ={0}.
{0},q:φ={0}.
解:①p或q:2+2=5或3>2 ;p且q:2+2=5且3>2 ;非p:2+2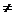 5.
5.
∵p假q真,∴“p或q”为真,“p且q”为假,“非p”为真.
②p或q:9是质数或8是12的约数;p且q:9是质数且8是12的约数;非p:9不是质数.
∵p假q假,∴“p或q”为假,“p且q”为假,“非p”为真.
③p或q:1∈{1,2}或{1}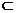 {1,2};p且q:1∈{1,2}且{1}
{1,2};p且q:1∈{1,2}且{1}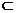 {1,2};非p:1
{1,2};非p:1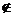 {1,2}.
{1,2}.
∵p真q真,∴“p或q”为真,“p且q”为真,“非p”为假.
④p或q:φ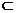 {0}或φ={0};p且q:φ
{0}或φ={0};p且q:φ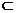 {0}且φ={0} ;非p:φ
{0}且φ={0} ;非p:φ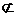 {0}.
{0}.
∵p真q假,∴“p或q”为真,“p且q”为假,“非p”为假.
2.“p且q”形式的复合命题
例2.如果p表示“5是10的约数”,q表示“5是15的约数”,r表示“5是8的约数”,试写出p且q,p且r的复合命题,并判断其真假,然后归纳出其规律.
解:p且q即“5是10的约数且是15的约数”为真(p、q为真);
p且r即“5是10的约数且是8的约数”为假(r为假)
小结:“p且q”形式的复合命题真假判断
当p、q为真时,p且q为真;当p、q中至少有一个为假时,p且q为假 可用下表表示
可用下表表示
|
p |
q |
p且q |
|
真 |
真 |
真 |
|
真 |
假 |
假 |
|
假 |
真 |
假 |
|
假 |
假 |
假 |
判断复合命题真假的方法
1.“非 p”形式的复合命题
例1 (1)如果p表示“2是10的约数”,试判断非p的真假.
(2) )如果p表示“3≤2”,那么非p表示什么?并判断其真假.
解:(1)中p表示的复合命题为真,而非p“2不是10的约数”为假.
(2)中p表示的命题“3≤2”为假,非p表示的命题为“3>2”,其显然为真.
小结:非p复合命题判断真假的方法
当p为真时,非p为假;当p为假时,非p为真,即“非 p”形式的复合命题的真假与p的真假相反,可用下表表示
|
p |
非p |
|
真 |
假 |
|
假 |
真 |
4.复合命题的构成形式是什么?
p或q(记作“p∨q” ); p且q(记作“p∨q” );非p(记作“┑q” ) 
3.什么叫做简单命题和复合命题?(不含有逻辑联结词的命题是简单命题由简单命题和逻辑联结词“或”、“且”、“非”构成的命题是复合命题 )
)
2.逻辑联结词是什么?(“或”的符号是“∨”、“且”的符号是“∧”、“非”的符号是“┑”,这些词叫做逻辑联结词)
含义是?“p或q”是指p,q中的任何一个或两者.例如,“x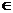 A或x
A或x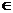 B”,是指x可能属于A但不属于B(这里的“但”等价于“且”),x也可能不属于A但属于B,x还可能既属于A又属于B(即x
B”,是指x可能属于A但不属于B(这里的“但”等价于“且”),x也可能不属于A但属于B,x还可能既属于A又属于B(即x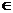 A3B);又如在“p真或q真”中,可能只有p真,也可能只有q真,还可能p,q都为真.
A3B);又如在“p真或q真”中,可能只有p真,也可能只有q真,还可能p,q都为真.
“p且q”是指p,q中的两者.例如,“x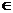 A且x
A且x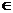 B”,是指x属于A,同时x也属于B(即x
B”,是指x属于A,同时x也属于B(即x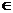 A
A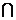 B).
B).
“非p”是指p的否定,即不是p. 例如,p是“x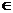 A”,则“非p”表示x不是集合A的元素(即x
A”,则“非p”表示x不是集合A的元素(即x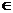
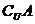 ).
).
1.什么叫做命题?(可以判断真假的语句叫命题 正确的叫真命题,错误的叫假命题
正确的叫真命题,错误的叫假命题 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com