
22.(本小题满分14分)
已知函数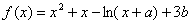 在x = 0处取得极值0.
在x = 0处取得极值0.
(1)求实数a,b的值;
(2)若关于x的方程,f(x)=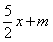 在区间[0,2]上恰有两个不同的实数根,求实数m的取值范围;
在区间[0,2]上恰有两个不同的实数根,求实数m的取值范围;
(3)证明:对任意的正整数n>1,不等式 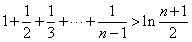 都成立.
都成立.
21.(本小题满分12分)
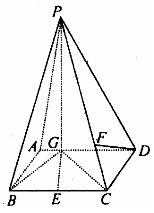
如图,四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形,
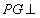 平面
平面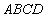 ,垂足为G,G在AD上,且
,垂足为G,G在AD上,且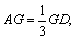
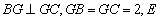 是
是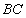 的中点,四面体
的中点,四面体
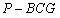 的体积为
的体积为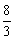 .
.
(1)求异面直线GE与PC所成的角;
(2)求点D到平面PBG的距离;
(3)若F点是PC上一点,且 求
求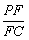 的值.
的值.
20.(本小题满分12分)
一种信号灯,只有符号“√”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“√”和“×”两者之一,其中出现“√”的概率为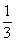 ,出现“×”的概率为
,出现“×”的概率为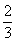 ,若第
,若第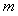 次出现“√”,记为
次出现“√”,记为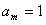 ,若第
,若第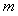 次出现“×”,则记为
次出现“×”,则记为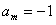 ,令
,令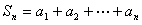 ,
,
 (1)求
(1)求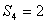 的概率;
的概率;
(2)求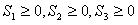 ,且
,且 的概率.
的概率.
19.(本小题满分12分)
已知二项式 。
。
(1)记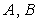 展开式中各项系数之和分别为
展开式中各项系数之和分别为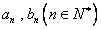 ,求
,求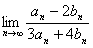 的值;
的值;
(2)若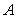 的展开式中第五项的系数与第三项的系数的比是10∶1,求展开式中系数最大的项和系数最小的项。
的展开式中第五项的系数与第三项的系数的比是10∶1,求展开式中系数最大的项和系数最小的项。
18.(本小题满分12分)
旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率
(2)求恰有2条线路没有被选择的概率.
(3)求选择甲线路旅游团数的数学期望.
17.(本小题满分12分)
设集合A={0,2,4,6},B={1,3,5,7},从集合A、B中各取2个元素组成没有重复数字的四位数.
(1)可组成多少个这样的四位数?
(2)有多少个是2的倍数或者是5的倍数?
16.由等式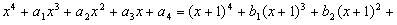
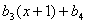
定义映射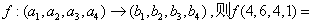 。
。
15.“渐升数”是指每个数字比其左边的数字大的正整数(如34689).若五位“渐升数”按从小到大的顺序排列,则第100个数为 。
14.已知二次函数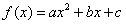 的导数为
的导数为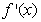 ,
,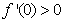 ,对于任意实数
,对于任意实数 都有
都有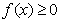 ,则
,则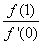 的最小值为
。
的最小值为
。
13.五位同学各自制作了一张贺卡,分别装入5个空白信封内,这五位同学每人随机地抽取一封,则恰好有两人抽取到的贺卡是其本人制作的概率是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com