
5.向量的应用
(1)会用向量方法解决某些简单的平面几何问题.
(2)会用向量方法解决简单的力学问题与其他一些实际问题.
4.平面向量的数量积
(1)理解平面向量数量积的含义及其物理意义.
(2)了解平面向量的数量积与向量投影的关系.
(3)掌握数量积的坐标表达式,会进行平面向量数量积的运算.
(4)能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.
3.平面向量的基本定理及坐标表示
(1) 了解平面向量的基本定理及其意义.
(2) 掌握平面向量的正交分解及其坐标表示.
(3)会用坐标表示平面向量的加法、减法与数乘运算.
(4) 理解用坐标表示的平面向量共线的条件.
2.向量的线性运算
(1) 掌握向量加法、减法的运算,并理解其几何意义.
(2) 掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.
(3) 了解向量线性运算的性质及其几何意义.
1.平面向量的实际背景及基本概念
(1)了解向量的实际背景.
(2)理解平面向量的概念,理解两个向量相等的含义.
(3)理解向量的几何表示.
(二)考点预测题
1(2007年山东高考题5).函数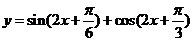 的最小正周期和最大值分别为( )
的最小正周期和最大值分别为( )
(A)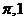 (B)
(B) 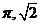 (C)
(C)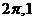 (D)
(D) 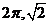
[解析]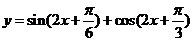
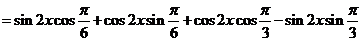
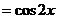 .
.
[答案]A.
2(山东济宁市2008-2009学年度质量检测4).已知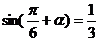 ,则
,则
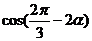 的值等于_______________.
的值等于_______________.
[解析]由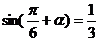 得:
得: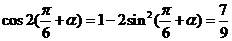 ,即
,即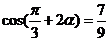 ,所以
,所以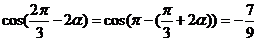 .
.
[答案]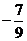 .
.
3(天津汉沽一中2008~2009届月考理15).已知向量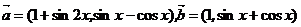 ,设函数
,设函数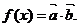
(Ⅰ)求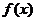 的最大值及相应的
的最大值及相应的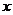 的值;
的值;
(Ⅱ)若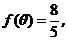 求
求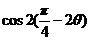 的值.
的值.
[解析]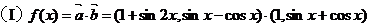
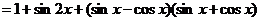
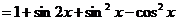
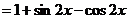
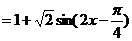
∴当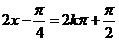 ,即
,即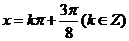 时,
时,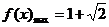 .
.
(Ⅱ)解法1:由(Ⅰ)知, 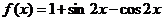
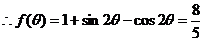 .
.
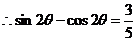 ,两边平方得
,两边平方得
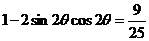 .
. 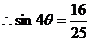
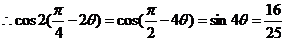 .
.
解法2:由(Ⅰ)知
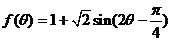
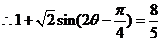
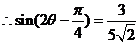
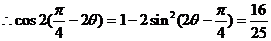 .
.
(一)考点预测
高考对三角恒等式部分的考查仍会是中低档题,无论是小题还是大题中出现都是较容易的.主要有三种可能:
(1)以小题形式直接考查:利用两角和与差以及二倍角公式求值、化简;
(2)以小题形式与三角函数、向量、解三角形等知识相综合考查两角和与差以及二倍角等公式;
(3)以解答题形式与三角函数、向量、解三角形、函数等知识相综合考查,对三角恒等变换的综合应用也可能与解三角形一起用于分析解决实际问题的应用问题,主要考查综合运用数学知识分析问题和解决问题的能力。
复习时要重视相关的思想方法,如数形结合思想、特值法、构造法、等价转换法等.
1(天津汉沽一中2009届高三月考文8).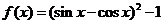 是( )
是( )
A.最小正周期为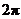 的偶函数 B.最小正周期为
的偶函数 B.最小正周期为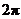 的奇函数
的奇函数
C.最小正周期为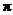 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为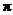 的奇函数
的奇函数
[解析]∵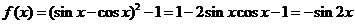
∴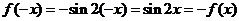 ,
,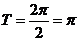 .
.
[答案]D.
2(2008~2009学年福建厦门质检四).已知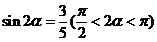 ,
,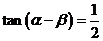 ,则
,则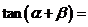 ( )
( )
A. 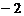 B.
B.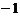 C.
C.
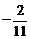 D.
D.
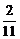
[解析]由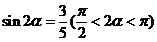 得
得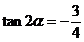 ,
,
又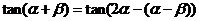
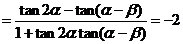 .
.
[答案]A.
3(2008~2009学年宁夏5). 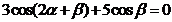 ,由
,由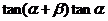 的值为( )
的值为( )
A.±4 B.4 C.-4 D.1
[解析]由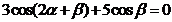 得:
得: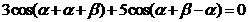 ,
,
即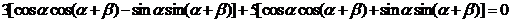
所以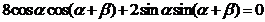 ,所以
,所以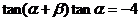 .
.
[答案]C.
4 (苏州市2009届高三教学调研测试13) .在锐角△ABC中,b=2,B=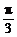 ,
,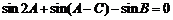 ,则△ABC的面积为_________.
,则△ABC的面积为_________.
[解析]由条件得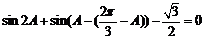 ,
,
则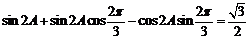 ,
,
则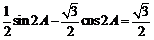 ,
,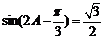 ,
,
又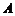 为锐角,所以
为锐角,所以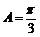 ,所以△ABC为等边三角形,面积为
,所以△ABC为等边三角形,面积为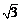 .
.
[答案]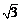 .
.
5(2008-2009学年度广东六校第三次联考理12).已知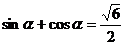
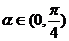 ,
,
则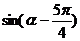 =
.
=
.
[解析]由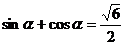 得
得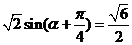 ,
,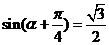 ,
,
又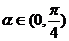 ,所以
,所以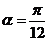 ,所以
,所以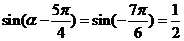 .
.
[答案]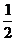 .
.
6(山东省临沂市08-09学年度模拟试题17).已知函数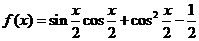 .
.
(Ⅰ)若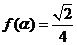 ,
,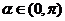 ,求
,求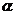 的值;
的值;
(Ⅱ)求函数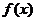 在
在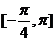 上最大值和最小值.
上最大值和最小值.
[解析](Ⅰ)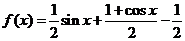
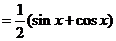
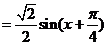
由题意知: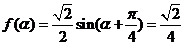 ,即
,即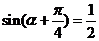 .
.
∵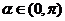 ,即
,即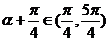 ,
,
∴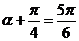 ,
,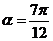 .
.
(Ⅱ)∵
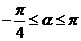 ,
即
,
即 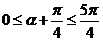 ,
,
∴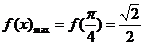 ,
,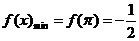 .
.
7(辽宁省部分重点中学协作体2008年高考模拟).已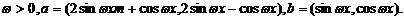
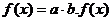 图像上相邻的两个对称轴的距离是
图像上相邻的两个对称轴的距离是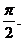
(1)求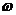 的值;
的值;
(2)求函数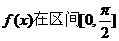 上的最大值和最小值.
上的最大值和最小值.
[解析]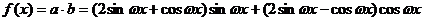 ……(2分)
……(2分)
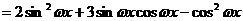

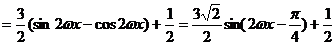 …………6分
…………6分
(1)因为函数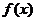 的图象上相邻的两个对称轴间的距离是
的图象上相邻的两个对称轴间的距离是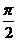
所以函数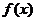 的最小正周期T=
的最小正周期T=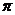 ,则
,则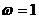 ………………8分
………………8分
(2)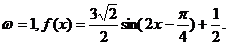
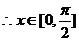
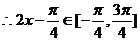 ,
,
则当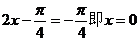 时,
时,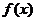 取得最小值-1;
取得最小值-1;
当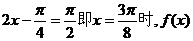 取得最大值
取得最大值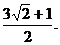 …………12分
…………12分
8 (天津一中2008-2009月考理17).已知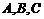 为锐角
为锐角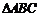 的三个内角,两向量
的三个内角,两向量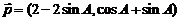 ,
,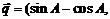
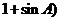 ,若
,若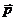 与
与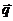 是共线向量.
是共线向量.
(1)求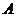 的大小;
的大小;
(2)求函数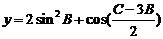 取最大值时,
取最大值时,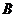 的大小.
的大小.
[解析](1)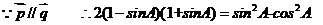
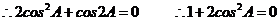
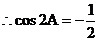
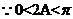 ,
,
(2)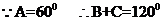
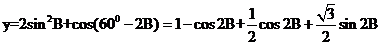
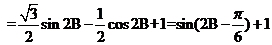
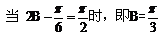 .
.
9(2009连云港市高三年级第二次调研考试数学模拟试题15) .设向量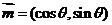 ,
,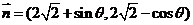 ,
,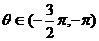 ,若
,若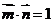 ,
,
求:(1)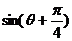 的值;
(2)
的值;
(2)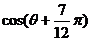 的值.
的值.
[解析](1)依题意,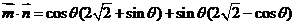
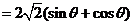
 ,又
,又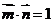
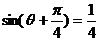 .
.
(2)由于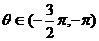 ,则
,则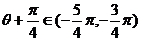
结合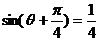 ,可得
,可得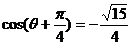
则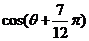
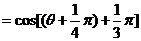
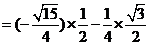
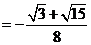 .
.
1.(2007年宁夏、海南文9).若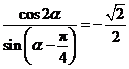 ,则
,则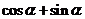 的值为( )
的值为( )
A.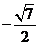 B.
B.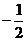 C.
C.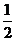 D.
D.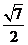
[解析]由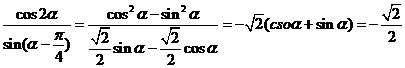 ,
,
∴sinα+cosα=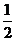 .
.
[答案]C.
2(2008年高考海南卷7).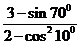 =( C )
=( C )
A. 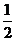 B.
B. 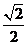 C.
2 D.
C.
2 D. 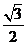
[解析]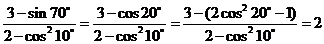 .
.
[答案]C.
3(2007年江苏卷11).若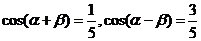 ,则
,则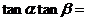 .
.
[解析]由条件得: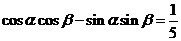 ,
,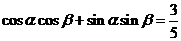 ,
,
所以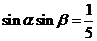 ,
,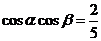 ,所以
,所以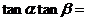
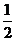 .
.
[答案]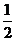 .
.
4(2007浙江理12).已知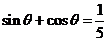 ,且
,且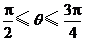 ,则
,则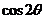 的值是 .
的值是 .
[解析]将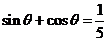 两边平方得
两边平方得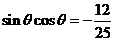 ,
,
所以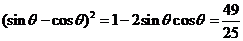 ,则
,则 ,
,
又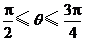 ,所以
,所以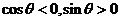 ,所以
,所以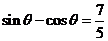 ,
,
故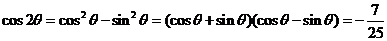 .
.
[答案] .
.
5(2008年广东卷理12).已知函数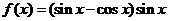 ,
,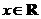 ,则
,则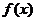 的最小正周期是
.
的最小正周期是
.
[解析]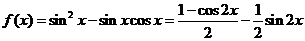 ,此时可得函数的最小正周期
,此时可得函数的最小正周期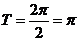 .
.
[答案]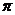 .
.
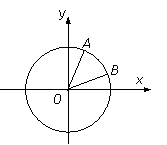 6(2008年江苏卷15).如图,在平面直角坐标系
6(2008年江苏卷15).如图,在平面直角坐标系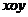 中,以
中,以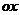 轴为始边做两个锐角
轴为始边做两个锐角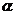 ,
,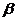 ,它们的终边分别与单位圆相交于A,B 两点,已知A,B 的横坐标分别为
,它们的终边分别与单位圆相交于A,B 两点,已知A,B 的横坐标分别为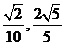 .
.
(Ⅰ)求tan(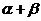 )的值;
)的值;
(Ⅱ)求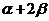 的值.
的值.
[解析]由条件的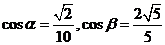 ,因为
,因为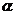 ,
,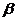 为锐角,所以
为锐角,所以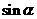 =
=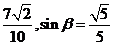
因此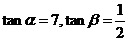
(Ⅰ)tan(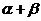 )=
)=
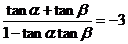
(Ⅱ) 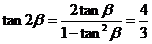 ,所以
,所以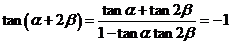
∵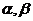 为锐角,∴
为锐角,∴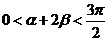 ,∴
,∴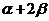 =
=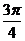 。
。
7(2008年福建卷17)已知向量m=(sinA,cosA),n=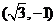 ,m·n=1,且A为锐角.
,m·n=1,且A为锐角.
(Ⅰ)求角A的大小;
(Ⅱ)求函数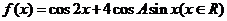 的值域.
的值域.
[解析](Ⅰ)由题意得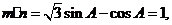
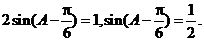
由A为锐角得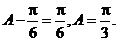
(Ⅱ)由(Ⅰ)知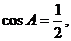
所以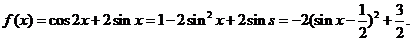
因为x∈R,所以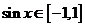 ,因此,当
,因此,当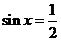 时,f(x)有最大值
时,f(x)有最大值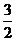 .
.
当sinx=-1时,f(x)有最小值-3,所以所求函数f(x)的值域是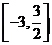 .
.
2.简单的三角恒等变换
能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com