
2.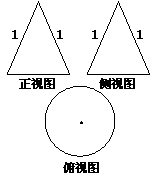 (宁夏区银川一中2008届高三年级第五次月考测试,数学理科,12)如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是 ( )
(宁夏区银川一中2008届高三年级第五次月考测试,数学理科,12)如图,一个几何体的正视图和侧视图是腰长为1的等腰三角形,俯视图是一个圆及其圆心,当这个几何体的体积最大时圆的半径是 ( )
A.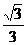 B.
B.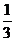 C.
C.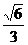 D.
D.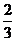
[解析]本题考查三视图及椎体的体积计算。设底面半径为,高位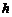 ,又
,又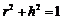 ,则
,则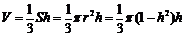 ,当
,当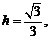 即
即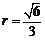 时,体积最大。
时,体积最大。
[答案]C
1.(山东省烟台市2008年高三适应性练习(三),数学理科,6)已知直线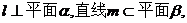 则下列四个命题:
则下列四个命题:
①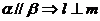 ; ②
; ②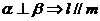 ;
;
③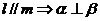 ; ④
; ④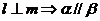
其中正确的是 ( )
A.①② B.③④ C.②④ D.①③
[解析]本题考查线面位置关系的判断,②④显然不正确
[答案]D
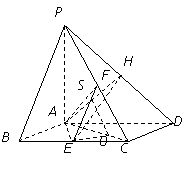
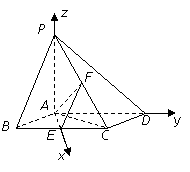
7.(2008年山东卷,数学理科,20)如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,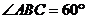 ,E,F分别是BC, PC的中点.
,E,F分别是BC, PC的中点.
(Ⅰ)证明:AE⊥PD;
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为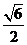 ,求二面角E-AF-C的余弦值.
,求二面角E-AF-C的余弦值.
[解析]本题考查线线垂直的证明,和二面角的求法,理科生应学会利用空间向量解决问题。
[答案](Ⅰ)证明:由四边形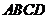 为菱形,
为菱形, ,可得
,可得 为正三角形.
为正三角形.
因为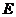 为
为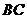 的中点,所以
的中点,所以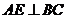 .
.
 又
又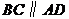 ,因此
,因此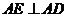 .
.
因为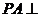 平面
平面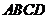 ,
,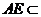 平面
平面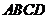 ,所以
,所以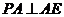 .
.
而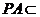 平面
平面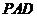 ,
, 平面
平面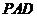 且
且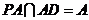 ,
,
所以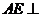 平面
平面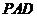 .又
.又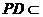 平面
平面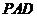 ,所以
,所以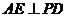 .
.
(Ⅱ)解:设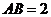 ,
, 为
为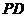 上任意一点,连接
上任意一点,连接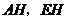 .
.
由(Ⅰ)知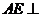 平面
平面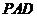 ,
,
则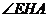 为
为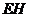 与平面
与平面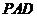 所成的角.
所成的角.
在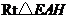 中,
中,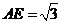 ,
,
所以当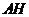 最短时,
最短时,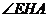 最大,
最大,
即当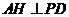 时,
时,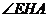 最大.
最大.
此时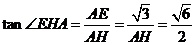 ,
,
因此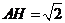 .又
.又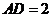 ,所以
,所以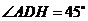 ,所以
,所以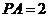 .
.
解法一:因为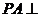 平面
平面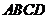 ,
,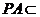 平面
平面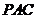 ,所以平面
,所以平面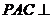 平面
平面 .
.
过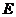 作
作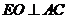 于
于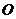 ,则
,则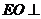 平面
平面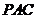 ,
,
过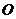 作
作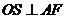 于
于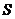 ,连接
,连接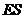 ,则
,则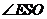 为二面角
为二面角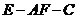 的平面角,
的平面角,
在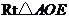 中,
中,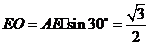 ,
,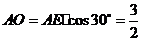 ,
,
又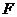 是
是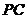 的中点,在
的中点,在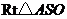 中,
中,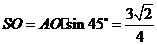 ,
,
又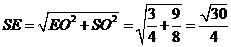 ,
,
在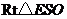 中,
中,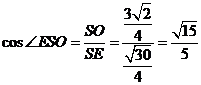 ,即所求二面角的余弦值为
,即所求二面角的余弦值为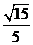 .
.
解法二:由(Ⅰ)知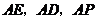 两两垂直,以
两两垂直,以 为坐标原点,建立如图所示的空间直角坐标系,又
为坐标原点,建立如图所示的空间直角坐标系,又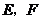 分别为
分别为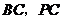 的中点,所以
的中点,所以
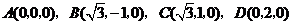 ,
,
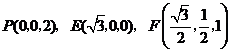 ,
,
所以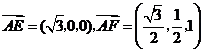 .
.
设平面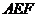 的一法向量为
的一法向量为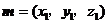 ,
,
则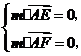 因此
因此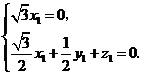 取
取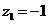 ,则
,则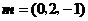 ,
,
因为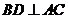 ,
,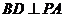 ,
,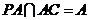 ,所以
,所以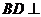 平面
平面 ,
,
故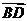 为平面
为平面 的一法向量.
的一法向量.
又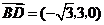 ,所以
,所以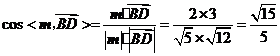 .
.
因为二面角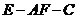 为锐角,所以所求二面角的余弦值为
为锐角,所以所求二面角的余弦值为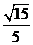 .
.
6.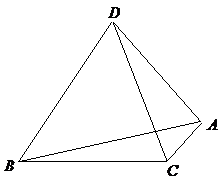 (2007年宁夏、 海南卷,数学文科,18)如图,
(2007年宁夏、 海南卷,数学文科,18)如图,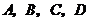 为空间四点.在
为空间四点.在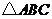 中,
中,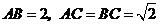 .
.
等边三角形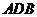 以
以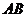 为轴运动.
为轴运动.
(Ⅰ)当平面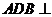 平面
平面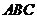 时,求
时,求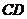 ;
;
(Ⅱ)当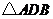 转动时,是否总有
转动时,是否总有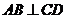 ?
?
证明你的结论.
[解析]考查直线和平面与平面和平面的相互关系
[答案](Ⅰ)取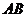 的中点
的中点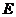 ,连结
,连结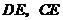 ,
,
 因为
因为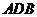 是等边三角形,所以
是等边三角形,所以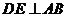 .
.
当平面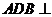 平面
平面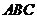 时,
时,
因为平面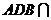 平面
平面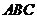
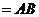 ,
,
所以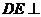 平面
平面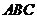 ,
,
可知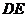
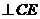
由已知可得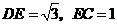 ,在
,在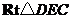 中,
中,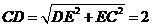 .
.
(Ⅱ)当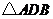 以
以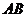 为轴转动时,总有
为轴转动时,总有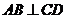 .
.
证明:
(ⅰ)当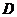 在平面
在平面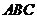 内时,因为
内时,因为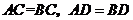 ,
,
所以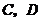 都在线段
都在线段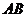 的垂直平分线上,即
的垂直平分线上,即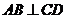 .
.
(ⅱ)当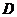 不在平面
不在平面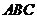 内时,由(Ⅰ)知
内时,由(Ⅰ)知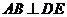 .又因
.又因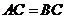 ,所以
,所以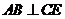 .
.
又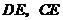 为相交直线,所以
为相交直线,所以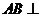 平面
平面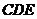 ,由
,由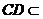 平面
平面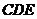 ,得
,得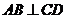 .
.
综上所述,总有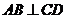 .
.
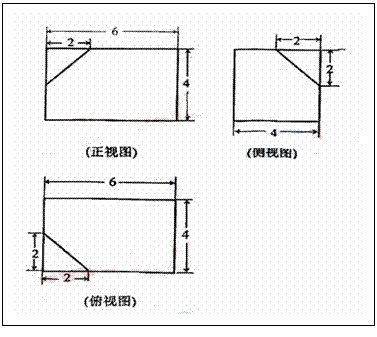
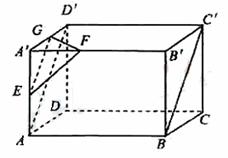
5.(2008年海南宁夏卷,数学文科,18)如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm)。(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积;(3)在所给直观图中连结 ,证明:
,证明: ∥面EFG。
∥面EFG。

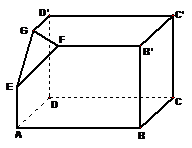
[解析]长方体的有关知识、体积计算及三视图的相关知识
[答案](1)如图
(2)所求多面体的体积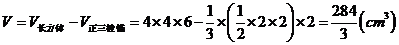
(3)证明:如图,在长方体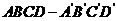 中,连接
中,连接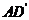 ,则
,则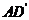 ∥
∥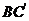
因为E,G分别为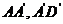 中点,所以
中点,所以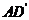 ∥
∥ ,从而
,从而 ∥
∥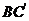 ,
,
又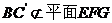 , 所以
, 所以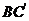 ∥平面EFG;
∥平面EFG;
4.(2007年广东卷,数学文科,6)若l、m、n是互不相同的空间直线,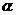 、
、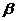 是不重合的平面,则下列命题中为真命题的是
是不重合的平面,则下列命题中为真命题的是
A.若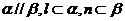 ,则
,则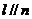 B.若
B.若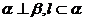 ,则
,则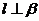
C. 若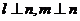 ,则
,则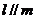 D.若
D.若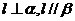 ,则
,则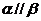
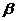
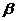
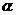
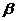
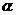 [解析]考查直线和平面与直线和平面的相互关系,对A,当 ∥ ,
[解析]考查直线和平面与直线和平面的相互关系,对A,当 ∥ ,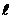
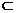 ?时,
?时,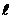 只是平行于 中某一直线而非所有,因而
只是平行于 中某一直线而非所有,因而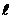 未必能平行于n;对B,只有在
未必能平行于n;对B,只有在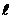 垂直与两面的交线才有结论
垂直与两面的交线才有结论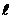 ⊥ 成立;
⊥ 成立;
对C,直线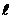 和m可以是异面,立方体的棱就能体现这种关系。
和m可以是异面,立方体的棱就能体现这种关系。
[答案]D
3.(2008年江西卷,数学理科,16) 如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有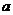 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点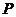 (图2)。有下列四个命题:
(图2)。有下列四个命题:
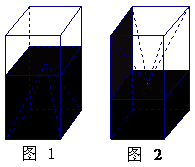 A.正四棱锥的高等于正四棱柱高的一半
A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点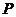
C.任意摆放该容器,当水面静止时,水面都恰好经过点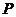
D.若往容器内再注入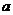 升水,则容器恰好能装满
升水,则容器恰好能装满
其中真命题的代号是: (写出所有真命题的代号).
[解析]易知所盛水的容积为容器容量的一半,故D正确,于是A错误;水平放置时由容器形状的对称性知水面经过点P,故B正确;C的错误可由图1中容器位置向右边倾斜一些可推知点P将露出水面。
[答案]真命题的代号是: BD 。
2.(2008年上海春卷,数学,8)已知一个凸多面体共有9个面,所有棱长均为1,其平面展开图如右图所示,则该凸多面体的体积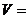 .
.
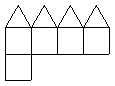 [解析]本题考查空间想象能力及相应几何体的体积,由题知,凸多面体是由一个棱为1的正四棱锥和一个棱长为1的正方体并接而成,正四棱锥的高为
[解析]本题考查空间想象能力及相应几何体的体积,由题知,凸多面体是由一个棱为1的正四棱锥和一个棱长为1的正方体并接而成,正四棱锥的高为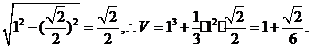
[答案]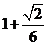
1.(2008年广东卷,数学理科,5,数学文科,7)将正三棱柱截去三个角(如图1所示 分别是
分别是 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
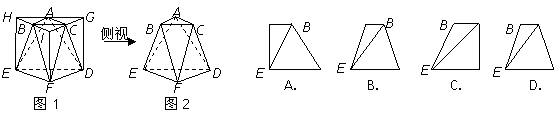

[解析]本题考查几何体的三视图,解题时在图2的右边放扇墙(心中有墙),可得答案.
[答案]A
09考试大纲中,对本节的要求如下:
(1)空间几何体
① 认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.
② 能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的立体模型,会用斜二测法画出它们的直观图.
③ 会用平行投影与中心投影两种方法,画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.
④ 会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求).
⑤ 了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).
(2)点、直线、平面之间的位置关系
① 理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理.
◆公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点在此平面内.
◆公理2:过不在同一条直线上的三点,有且只有一个平面.
◆公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
◆公理4:平行于同一条直线的两条直线互相平行.
◆定理:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
② 以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定定理.
理解以下判定定理.
◆如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
◆如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.
◆如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
◆如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.
理解以下性质定理,并能够证明.
◆如果一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行.
◆如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行.
◆垂直于同一个平面的两条直线平行.
◆如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直.
③ 能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com