
(二)考点预测题
1(2007年宁夏理4).已知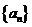 是等差数列,
是等差数列,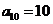 ,其前10项和
,其前10项和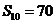 ,则其公差
,则其公差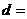 ( )
( )
A.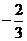 B.
B. C.
C.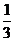 D.
D.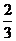
[解析]由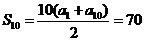 得a1=4, 则a10=a1+9d=4+9d=10,所以
得a1=4, 则a10=a1+9d=4+9d=10,所以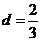 .
.
[答案]D.
2(2008年天津卷20).在数列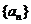 中,
中,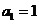 ,
,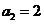 ,且
,且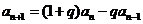 (
(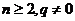 ).
).
(Ⅰ)设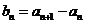 (
(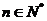 ),证明
),证明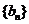 是等比数列;
是等比数列;
(Ⅱ)求数列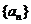 的通项公式;
的通项公式;
(Ⅲ)若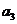 是
是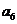 与
与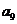 的等差中项,求
的等差中项,求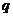 的值,并证明:对任意的
的值,并证明:对任意的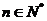 ,
,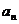 是
是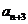 与
与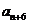 的等差中项.
的等差中项.
[解析](Ⅰ)证明:由题设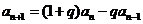 (
(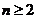 ),得
),得
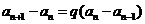 ,即
,即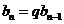 ,
,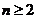 .
.
又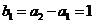 ,
,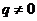 ,所以
,所以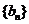 是首项为1,公比为
是首项为1,公比为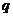 的等比数列.
的等比数列.
(Ⅱ)解法:由(Ⅰ)
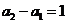 ,
,
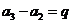 ,
,
……
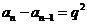 ,(
,(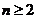 ).
).
将以上各式相加,得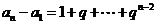 (
(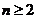 ).
).
所以当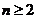 时,
时,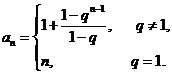
上式对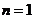 显然成立.
显然成立.
(Ⅲ)解:由(Ⅱ),当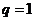 时,显然
时,显然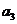 不是
不是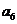 与
与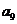 的等差中项,故
的等差中项,故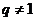 .
.
由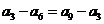 可得
可得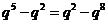 ,由
,由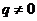 得
得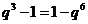 , ①
, ①
整理得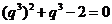 ,解得
,解得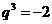 或
或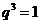 (舍去).于是
(舍去).于是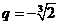 .
.
另一方面,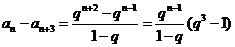 ,
,
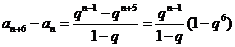 .
.
由①可得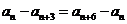 ,
,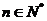 .
.
所以对任意的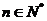 ,
,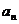 是
是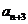 与
与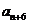 的等差中项.
的等差中项.
3(2008年辽宁卷21).在数列 ,
,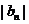 中,a1=2,b1=4,且
中,a1=2,b1=4,且 成等差数列,
成等差数列,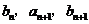 成等比数列(
成等比数列(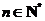 )
)
(Ⅰ)求a2,a3,a4及b2,b3,b4,由此猜测 ,
,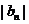 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(Ⅱ)证明: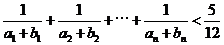 .
.
[解析](Ⅰ)由条件得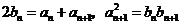
由此可得
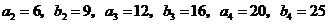 .
.
猜测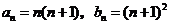 .
.
用数学归纳法证明:
①当n=1时,由上可得结论成立.
②假设当n=k时,结论成立,即
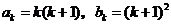 ,
,
那么当n=k+1时,
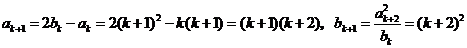 .
.
所以当n=k+1时,结论也成立.
由①②,可知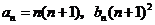 对一切正整数都成立.
对一切正整数都成立.
4(2008-2009学年江苏省盐城市高三数学上学期第一次月考20).已知数列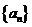 和
和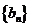 满足
满足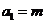 ,
,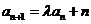 ,
,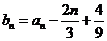 .
.
(Ⅰ) 当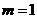 时,求证: 对于任意的实数
时,求证: 对于任意的实数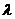 ,
,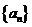 一定不是等差数列;
一定不是等差数列;
(Ⅱ) 当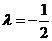 时,试判断
时,试判断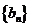 是否为等比数列;
是否为等比数列;
(Ⅲ) 设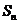 为数列
为数列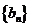 的前
的前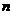 项和,在(Ⅱ)的条件下,是否存在实数
项和,在(Ⅱ)的条件下,是否存在实数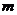 ,使得对任意的正
,使得对任意的正
整数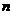 ,都有
,都有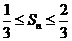 ?若存在,请求出
?若存在,请求出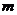 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
[解析](Ⅰ)当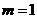 时,
时,
假设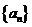 是等差数列,由
是等差数列,由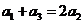 得
得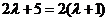 ,即5=2,矛盾.
,即5=2,矛盾.
故对于任意的实数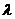 ,
,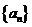 一定不是等差数列.
一定不是等差数列.
(Ⅱ)当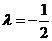 时,
时,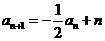 .而
.而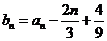 ,所以
,所以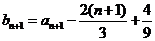
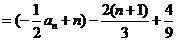 =
=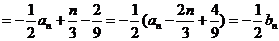 .
.
又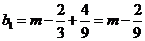 .
.
故当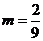 时,
时, 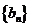 不是等比数列.
不是等比数列.
当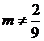 时,
时, 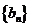 是以
是以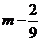 为首项,
为首项,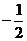 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(Ⅱ)知,当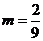 时,
时,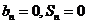 ,不合要求.
,不合要求.
所以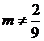 ,于是
,于是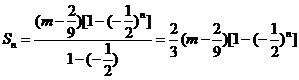 ,要使
,要使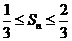 成立,
成立,
则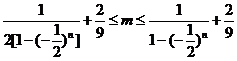 .
.
令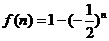 ,当n正奇数时,
,当n正奇数时,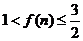 ;当n正偶数时,
;当n正偶数时,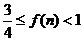 .
.
故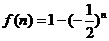 的最大值为
的最大值为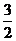 ,最小值为
,最小值为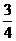 .
.
欲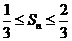 对任意的正整数n都成立,则
对任意的正整数n都成立,则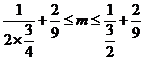 ,即
,即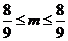 ,所以
,所以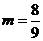 .
.
综上所述,存在唯一的实数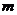 =
=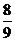 ,使得对任意的正整数
,使得对任意的正整数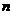 ,都有
,都有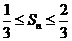 .
.
(一)等差数列、等比数列的通项公式、求和公式的应用以及等差、等比数列的基本性质一直是高考的重点内容,也会是今年高考的重点.对数列部分的考查一方面以小题考查数列的基本知识;另一方面以解答题形式考查等差、等比数列的概念、通项公式以及前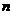 项和公式.解答题作为压轴题的可能性较大,与不等式、数学归纳法、函数等一起综合考查学生运用数学知识进行归纳、总结、推理、论证、运算等能力以及分析问题、解决问题的能力.具体地:
项和公式.解答题作为压轴题的可能性较大,与不等式、数学归纳法、函数等一起综合考查学生运用数学知识进行归纳、总结、推理、论证、运算等能力以及分析问题、解决问题的能力.具体地:
1. 数列中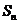 与
与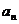 的关系一直是高考的热点,求数列的通项公式是最为常见的题目,要切实注意
的关系一直是高考的热点,求数列的通项公式是最为常见的题目,要切实注意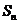 与
与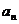 的关系.
的关系.
2.探索性问题在数列中考查较多,试题没有给出结论,需要考生猜出或自己找出结论,然后给以证明.探索性问题对分析问题解决问题的能力有较高的要求.
3.等差、等比数列的基本知识必考.这类考题既有选择题、填空题,又有解答题;有容易题、中等题,也有难题。
4.求和问题也是常见的试题,等差数列、等比数列及可以转化为等差、等比数列求和问题应掌握,还应该掌握一些特殊数列的求和.
5.将数列应用题转化为等差、等比数列问题也是高考中的重点和热点,从本章在高考中所占的分值来看,一年比一年多,而且都注重能力的考查.
6.有关数列与函数、数列与不等式、数列与概率等问题既是考查的重点,也是考查的难点.另外数列与程序框图的综合题也应引起重视.
1(天津市汉沽一中2009届月考文7).已知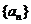 是等差数列,
是等差数列,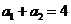 ,
,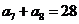 ,则该数列前10项和
,则该数列前10项和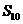 等于( )
等于( )
A.64 B.100 C.110 D.120
[解析]设公差为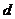 ,则由已知得
,则由已知得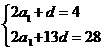 ,
,
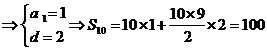 .
.
[答案]B.
2(辽宁省部分重点中学协作体2008年高考模拟).设等差数列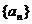 的前n项和为
的前n项和为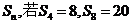 ,则
,则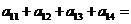 ( )
( )
A.18 B.17 C.16 D.15
[解析]等差数列中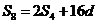 ,公差
,公差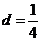 ,
,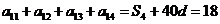 .[答案]A.
.[答案]A.
3(宁波市2008学年度第一学期期末试卷10).如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次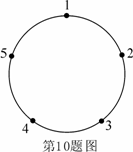 沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从
沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从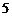 这点开始跳,则经2009次跳后它停在的点所对应的数为( )
这点开始跳,则经2009次跳后它停在的点所对应的数为( )
A.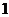 B.
B.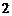 C.
C.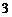 D.
D.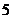
[解析]5-2-1-3-5,周期为4,2009=4×502+1,经过2009次跳后它停在的点所对应的数为2.
[答案]B.
4(2008~2009学年福建高考样卷·理).已知等比数列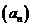 中
中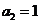 ,则其前3项的和
,则其前3项的和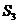 的取值范围是( )
的取值范围是( )
A.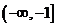 B.
B.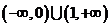 C.
C.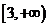 D.
D.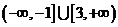
[解析]设公比为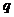 ,
,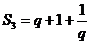 ,由
,由 或
或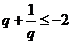 ,所以取值范围为
,所以取值范围为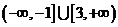 .
.
[答案]D.
5(2008~2009学年福州质检·理).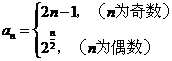 ,则
,则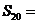
[解析]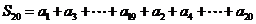
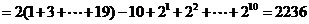 .
.
[答案]2236.
6(温州十校2008学年度第一学期期中高三数学试题理).已知数列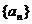 的前n项的和
的前n项的和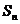 满足
满足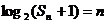 ,则
,则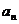 =
.
=
.
[解析]由条件得: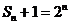 ,
,
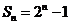 ,则
,则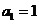 ,
,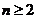 时,
时,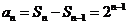 .
.
[答案]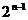 .
.
7(浙江省杭州市2009年第一次高考科目教学质量检测数学试题卷理科).数列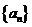 中,
中,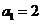 ,
,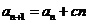 (
(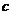 是不为零的常数,
是不为零的常数,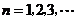 ),且
),且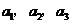 成等比数列.
成等比数列.
(1)求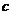 的值;
的值;
(2)求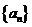 的通项公式;
的通项公式;
(3)求数列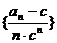 的前
的前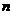 项之和
项之和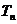 .
.
[解析](1)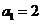 ,
,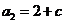 ,
,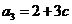 ,
,
因为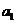 ,
,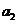 ,
,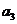 成等比数列,
成等比数列,
所以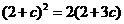 ,
,
解得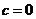 或
或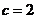 .
.
∵c≠0,∴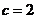 .
.
(2)当 时,由于
时,由于
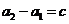 ,
,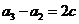 ,
,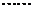
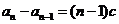 ,
,
所以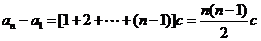 .
.
又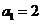 ,
,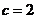 ,故
,故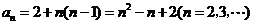 .
.
当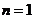 时,上式也成立,
时,上式也成立,
所以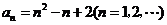 .
.
(3)令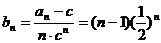
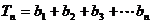
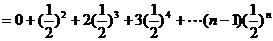 ……①
……①
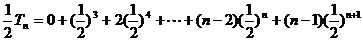 ……②
……②
①-②得: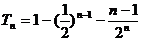
8(一中2008-2009月考理18).已知数列{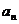 }中,
}中,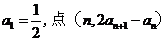 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(1)令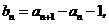 求证数列
求证数列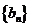 是等比数列;
是等比数列;
(2)求数列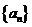 的通项;
的通项;
⑶ 设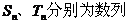
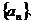
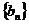 的前n项和,是否存在实数
的前n项和,是否存在实数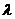 ,使得数列
,使得数列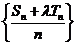 为等差数列?若存在,试求出
为等差数列?若存在,试求出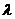 .若不存在,则说明理由.
.若不存在,则说明理由.
[解析](I)由已知得
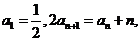
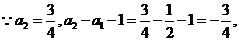
又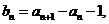
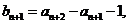
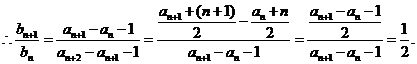
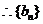 是以
是以 为首项,以
为首项,以 为公比的等比数列.
为公比的等比数列.
(II)由(I)知,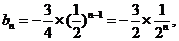
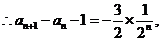
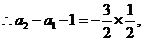
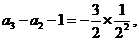
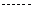
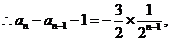
将以上各式相加得:
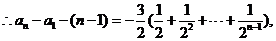
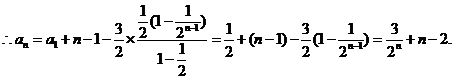
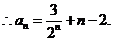
(III)解法一:
存在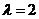 ,使数列
,使数列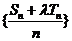 是等差数列.
是等差数列.
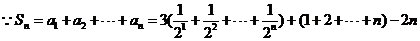
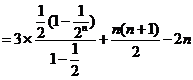
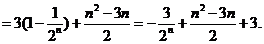
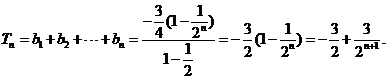
数列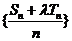 是等差数列的充要条件是
是等差数列的充要条件是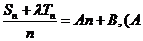 、
、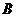 是常数
是常数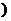
即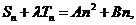
又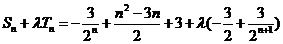
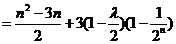
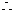 当且仅当
当且仅当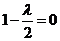 ,即
,即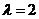 时,数列
时,数列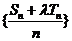 为等差数列.
为等差数列.
解法二:
存在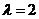 ,使数列
,使数列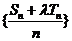 是等差数列.
是等差数列.
由(I)、(II)知,
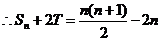
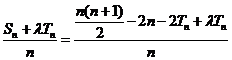
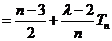
又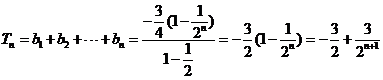
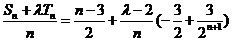
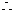 当且仅当
当且仅当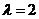 时,数列
时,数列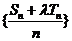 是等差数列.
是等差数列.
9(2008-2009学年山东师大附中高三数学模拟考试试题文科数学21).已知函数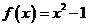 ,设曲线
,设曲线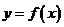 在点
在点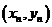 处的切线与
处的切线与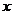 轴的交点为
轴的交点为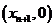 ,其中
,其中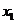 为正实数
(1)用
为正实数
(1)用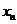 表示
表示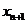 ;
(2)
;
(2)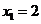 ,若
,若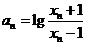 ,试证明数列
,试证明数列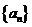 为等比数列,并求数列
为等比数列,并求数列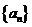 的通项公式;
(3)若数列
的通项公式;
(3)若数列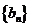 的前
的前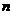 项和
项和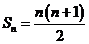 ,记数列
,记数列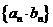 的前
的前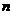 项和
项和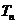 ,求
,求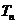 .
[解析](1)由题可得
.
[解析](1)由题可得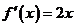 ,所以在曲线上点
,所以在曲线上点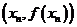 处的切线方程为
处的切线方程为
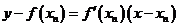 ,即
,即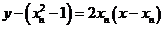
令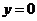 ,得
,得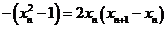 ,即
,即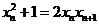
由题意得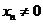 ,所以
,所以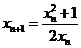
(2)因为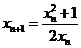 ,所以
,所以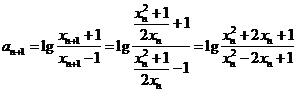
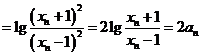
即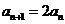 ,所以数列
,所以数列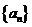 为等比数列故
为等比数列故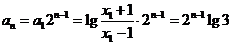 ---8分
---8分
(3)当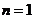 时,
时,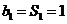
当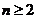 时,
时,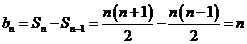
所以数列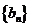 的通项公式为
的通项公式为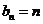 ,故数列
,故数列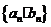 的通项公式为
的通项公式为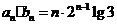
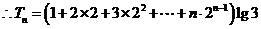 ①
①
①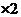 的
的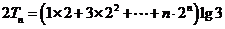 ②
②
①②得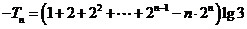
故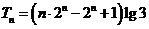 .
.
10(广州市越秀区2009年高三摸底调研理21).已知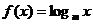 (m为常数,m>0且
(m为常数,m>0且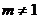 ),设
),设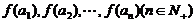 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.
(1)求证:数列{an}是等比数列;
(2)若bn=an·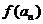 ,且数列{bn}的前n项和Sn,当
,且数列{bn}的前n项和Sn,当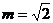 时,求Sn;
时,求Sn;
(3)若cn=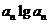 ,问是否存在m,使得{cn}中每一项恒小于它后面的项?
,问是否存在m,使得{cn}中每一项恒小于它后面的项?
若存在,求出m的范围;若不存在,说明理由.
[解析](1)由题意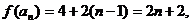 即
即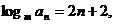
∴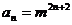
∴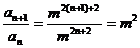 ∵m>0且
∵m>0且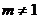 ,∴m2为非零常数,
,∴m2为非零常数,
∴数列{an}是以m4为首项,m2为公比的等比数列
(2)由题意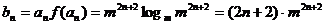 ,
,
当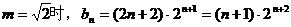
∴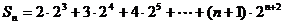 ①
①
①式两端同乘以2,得
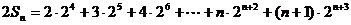 ②
②
②-①并整理,得
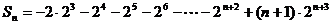
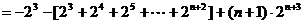
=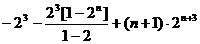
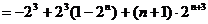
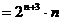 …10分
…10分
(3)由题意 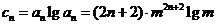
要使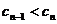 对一切
对一切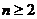 成立,即
成立,即 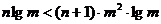 对一切
对一切
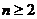 成立,
成立,
①当m>1时, 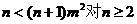 成立;
成立;
②当0<m<1时,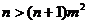
∴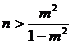 对一切
对一切
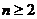 成立,只需
成立,只需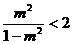 ,
,
解得  , 考虑到0<m<1, ∴0<m<
, 考虑到0<m<1, ∴0<m<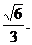
综上,当0<m<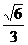 或m>1时,数列{cn}中每一项恒小于它后面的项.
或m>1时,数列{cn}中每一项恒小于它后面的项.
1(2008年广东卷2).记等差数列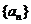 的前
的前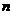 项和为
项和为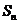 ,若
,若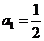 ,
,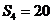 ,则
,则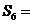 ( )
( )
A.16 B.24 C.36 D.48
[解析]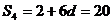 ,
,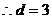 ,故
,故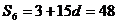 .
.
[答案]D.
2(2008年浙江卷6).已知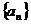 是等比数列,
是等比数列,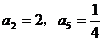 ,则
,则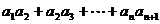 =( )
=( )
(A)16(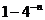 )
(B)16(
)
(B)16(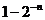 )
)
(C)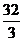 (
(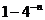 )
(D)
)
(D)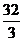 (
(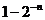 )
)
[解析]由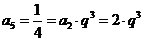 ,解得
,解得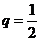 ,
,
数列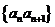 仍是等比数列:其首项是
仍是等比数列:其首项是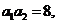 公比为
公比为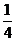 ,
,
所以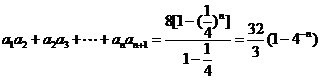 .
.
[答案]C.
3(2007年天津理8).设等差数列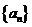 的公差
的公差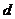 不为0,
不为0,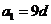 .若
.若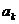 是
是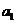 与
与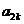 的等比中项,则
的等比中项,则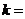 ( )
( )
A.2 B.4 C.6 D.8
[解析]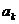 是
是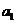 与
与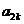 的等比中项,则
的等比中项,则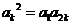 ,
,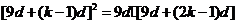
又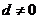 ,则
,则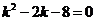 ,
,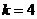 (舍负).
(舍负).
[答案]B.
4(2008年江苏卷10).将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
. . . . . . .
按照以上排列的规律,第n 行(n ≥3)从左向右的第3 个数为 .
[解析]前n-1 行共有正整数1+2+…+(n-1)个,即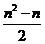 个,因此第n 行第3 个数是全体正整数中第
个,因此第n 行第3 个数是全体正整数中第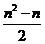 +3个,即为
+3个,即为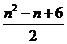 .
.
[答案]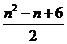 .
.
5(2007年浙江文19) .已知数列{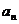 }中的相邻两项
}中的相邻两项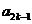 、
、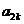 是关于x的方程
是关于x的方程
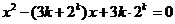 的两个根,且
的两个根,且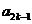 ≤
≤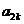 (k =1,2,3,…).
(k =1,2,3,…).
(I)求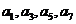 及
及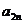 (n≥4)(不必证明);
(n≥4)(不必证明);
(Ⅱ)求数列{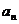 }的前2n项和S2n.
}的前2n项和S2n.
[解析] (I)方程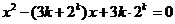 的两个根为
的两个根为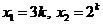 .
.
当k=1时,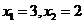 ,所以
,所以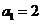 ;
;
当k=2时,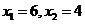 ,所以
,所以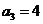 ;当k=3时,
;当k=3时,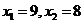 ,所以
,所以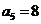 ;
;
当k=4时,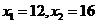 ,所以
,所以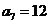 ;
;
因为n≥4时,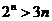 ,所以
,所以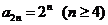
(Ⅱ)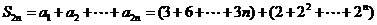
=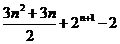 .
.
6(2007年山东理17).设数列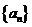 满足
满足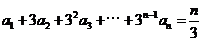 ,
,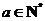 .
.
(Ⅰ)求数列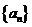 的通项;
的通项;
(Ⅱ)设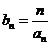 ,求数列
,求数列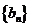 的前
的前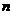 项和
项和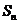 .
.
[解析](I)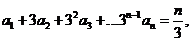
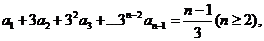
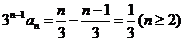 ,
,
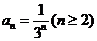 .
.
验证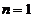 时也满足上式,
时也满足上式,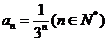 .
.
 (II)
(II) 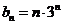 ,
,
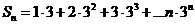 ,
,
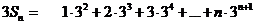 ,
,
则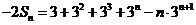
 ,
,
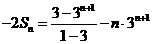 ,所以
,所以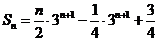 .
.
7(2008年安徽卷21).设数列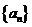 满足
满足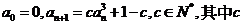 为实数
为实数
(Ⅰ)证明: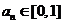 对任意
对任意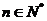 成立的充分必要条件是
成立的充分必要条件是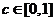 ;
;
(Ⅱ)设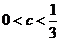 ,证明:
,证明: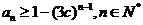 ;
;
(Ⅲ)设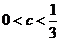 ,证明:
,证明: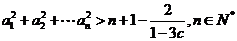
[解析](Ⅰ)必要性 :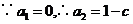 ,
,
又 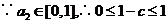 ,即
,即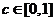
充分性 :设 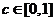 ,对
,对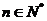 用数学归纳法证明
用数学归纳法证明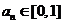
当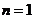 时,
时,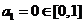 .假设
.假设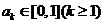
则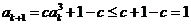 ,且
,且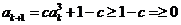
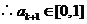 ,由数学归纳法知
,由数学归纳法知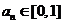 对所有
对所有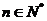 成立
成立
(Ⅱ) 设 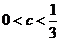 ,当
,当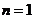 时,
时,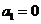 ,结论成立
,结论成立
当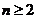 时,
时,
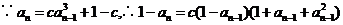
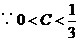 ,由(1)知
,由(1)知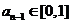 ,所以
,所以 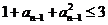 且
且 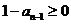
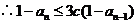
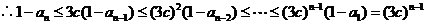
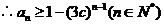
(Ⅲ)设 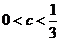 ,当
,当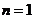 时,
时,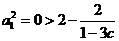 ,结论成立
,结论成立
当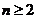 时,由(2)知
时,由(2)知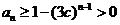
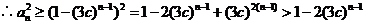
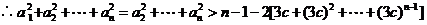
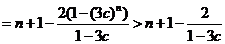 .
.
2.等差数列、等比数列
(1) 理解等差数列、等比数列的概念.
(2)掌握等差数列、等比数列的通项公式与前n项和公式.
(3)能在具体的问题情境中识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.
④ 了解等差数列与一次函数、等比数列与指数函数的关系.
高考对数列的考查比较全面,重点是等差、等比数列的定义、通项公式、前n项和公式、等差(比)中项及等差和等比数列性质的灵活运用;在能力要求上,主要考查学生的运算能力,逻辑思维能力以及分析问题和解决问题的能力,其中考查思维能力是支柱,运算能力是主体,应用是归宿.
主要考点有:
1.数列的概念和简单表示法
(1)了解数列的概念和几种简单的表示方法(列表、图像、通项公式).
(2)了解数列是自变量为正整数的一类函数.
(二)考点预测题
1(2008年江苏卷5).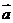 ,
,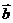 的夹角为
的夹角为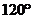 ,
,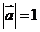 ,
,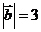 则
则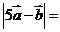 .
.
[解析]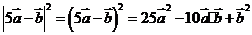 =
=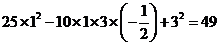 ,则
,则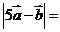 7.
7.
[答案]7.
2(2007年山东理11). 在直角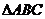 中,
中,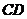 是斜边
是斜边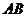 上的高,则下列等式不成立的是( )
上的高,则下列等式不成立的是( )
A.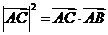 B.
B.
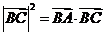
C.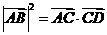 D.
D.
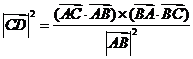
[解析]由于
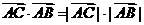 cso∠CAB=|
cso∠CAB=|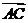 |2,
可排除A.
|2,
可排除A. 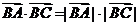 cos∠ABC=
cos∠ABC=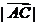 2,
可排除B , 而
2,
可排除B , 而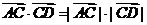 cos(π-∠ACD)=-|
cos(π-∠ACD)=-|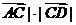 cos∠ACD<0 , |
cos∠ACD<0 , |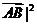 >0
, ∴|
>0
, ∴|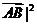 ≠
≠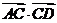 ,可知选C.
,可知选C.
[答案]C.
3(广东省2009届高三第一次六校联考(理)16).已知向量a=(sinθ,1),b=(1,cosθ),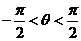 .
.
(Ⅰ)若a⊥b,求θ;
(Ⅱ)求|a+b|的最大值.
[解析](Ⅰ)若a⊥b,则sinθ+cosθ=0,
由此得 tanθ=-1(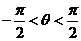 ),
),
所以 θ=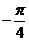 ;
;
(Ⅱ)由a=(sinθ,1),b=(1,cosθ),得
|a+b|==
=,
当sin(θ+)=1时,|a+b|取得最大值,
即当θ=时,|a+b|最大值为+1.
4(2009届广东五校高三第二联考试卷文) .已知向量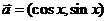 ,
,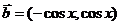 ,
,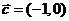 .
.
(1)若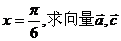 的夹角;
的夹角;
(2)当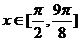 时,求函数
时,求函数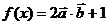 的最大值.
的最大值.
[解析](1)当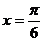 时,
时,
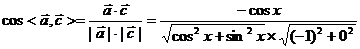
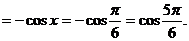
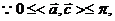
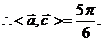
(2)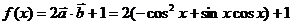
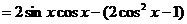
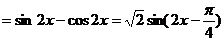 .
.
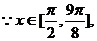 ∴
∴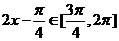 ,故
,故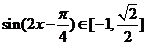
∴当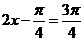 时,即
时,即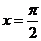 ,所以
,所以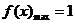 .
.
(一)文字介绍
预计向量基本概念、向量基本运算等基础问题,通常为选择题或填空题出现;而向量与三角函数、解三角形等综合的问题,通常为解答题,难度以中档题为主.具体如下:
1.向量概念和向量的基本定理
有关向量概念和向量的基本定理的命题,主要以选择题或填空题为主,考查的难度属中档类型.
2.向量的运算
向量的运算要求掌握向量的加减法运算,会用平行四边形法则、三角形法则进行向量的加减运算;掌握实数与向量的积运算,理解两个向量共线的含义,会判断两个向量的平行关系;掌握向量的数量积的运算,体会平面向量的数量积与向量投影的关系,并理解其几何意义,掌握数量积的坐标表达式,会进行平面向量积的运算,能运用数量积表示两个向量的夹角,会用向量积判断两个平面向量的垂直关系.主要以选择、填空题型出现,难度不大,考查重点为模和向量夹角的定义、夹角公式、向量的坐标运算,有时也会与其它内容相结合.
3.向量与三角函数的综合问题
向量与三角函数的综合问题是高考经常出现的问题,考查了向量的知识,三角函数的知识,达到了高考中试题的覆盖面的要求.命题以三角函数作为坐标,以向量的坐标运算或向量与解三角形的内容相结合,也有向量与三角函数图象平移结合的问题,属中档偏易题.
4.平面向量与函数问题的交汇
平面向量与函数交汇的问题,主要是向量与二次函数结合的问题为主,要注意自变量的取值范围.命题多以解答题为主,属中档题.
1(汉沽一中2008~2009届月考文9).已知平面向量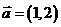 ,
, 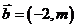 ,
且
,
且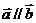 , 则
, 则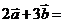 ( )
( )
A.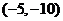 B.
B.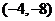 C.
C.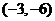 D.
D.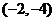
[解析]∵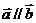 ,∴
,∴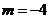 ,
,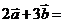
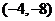 .
.
B.
 2(浙江省09年高考省教研室第一次抽样测试数学试题(理)5).已知
2(浙江省09年高考省教研室第一次抽样测试数学试题(理)5).已知 ,点P在直线AB上,且满足
,点P在直线AB上,且满足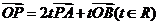 ,则
,则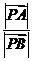 =( )
=( )
A、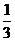 B、
B、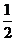 C、2
D、3
C、2
D、3
[解析]如图所示,不妨设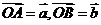 ;找共线,对于点P在直线AB上,有
;找共线,对于点P在直线AB上,有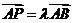 ;列方程,因此有
;列方程,因此有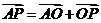
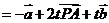 ,即
,即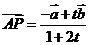 ;而
;而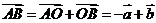 ,即有
,即有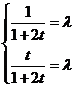 ,因此
,因此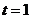 时
时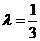 .即有
.即有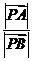 =
=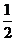 .
.
[答案]B.
3(沈阳二中2009届高三期末数学试题).设点P是△ABC所在平面内一点,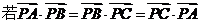 ,则点P是△ABC的( )
,则点P是△ABC的( )
A.内心 B.外心 C.重心 D.垂心
[解析]
[答案]D.
4(宁波市2008学年度第一学期高三期末数(文)).已知在平面直角坐标系中,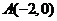 ,
,
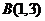 ,O为原点,且
,O为原点,且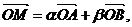 (其中
(其中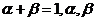 均为实数),若N(1,0),则
均为实数),若N(1,0),则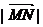 的最小值是 .
的最小值是 .
[解析]由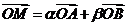 及
及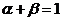 知,点M与点A、B共线,所以
知,点M与点A、B共线,所以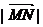 的最小值是点N到直线AB的距离,在直角三角形ABN中求解得
的最小值是点N到直线AB的距离,在直角三角形ABN中求解得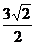 .
.
[答案]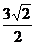 .
.
5(福州质检·理).已知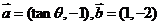 ,若
,若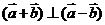 ,则
,则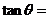 .
.
[解析]由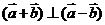 得:
得: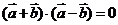 ,即
,即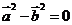 ,所以
,所以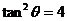 ,
,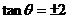 .
.
[答案]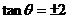 .
.
6(江苏省南通市2008-2009学年度第一学期期末调研测试数学试卷13) .在△ABC中,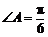 ,D是BC边上任意一点(D与B、C不重合),且
,D是BC边上任意一点(D与B、C不重合),且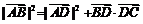 ,则
,则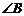 等于 ▲ .
等于 ▲ .
[解析]当点D无限逼近点C时,由条件知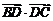 趋向于零,
趋向于零,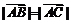 ,即△ABC是等边三角形.
,即△ABC是等边三角形.
[答案] 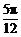 .
.
7 ( 江苏省常州市2008-2009高三第一学期期中统一测试10) .已知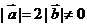 ,且关于
,且关于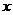 的函数
的函数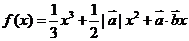 在R上有极值,则
在R上有极值,则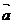 与
与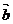 的夹角范围为_______.
的夹角范围为_______.
[解析]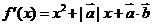 ,依题意
,依题意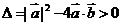 ,
,
即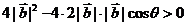 ,
,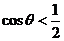 ,又夹角
,又夹角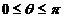 ,所以范围为
,所以范围为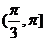 .
.
[答案]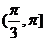 .
.
8(2008年东北三省三校高三第一次联合模拟考试).
已知向量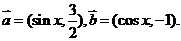
(1)当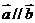 时,求
时,求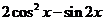 的值;
的值;
(2)求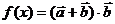 在
在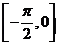 上的值域.
上的值域.
[解析](1)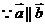 ,∴
,∴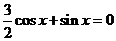 ,∴
,∴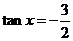
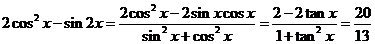 .
.
(2)
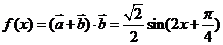
∵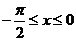 ,∴
,∴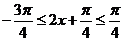 ,∴
,∴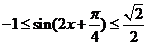
∴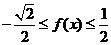 ∴函数
∴函数 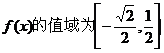 .
.
9(绍兴市2008学年第一学期统考数学试题).已知向量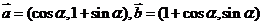 ,
,
(1)若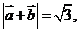 求
求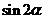 的值;
的值;
(2)设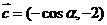 ,求
,求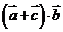 的取值范围.
的取值范围.
[解析](1)因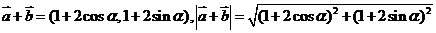
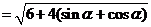 ,∴
,∴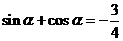 ,两边平方得
,两边平方得 ,
,
∴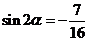 .
.
(2)因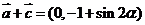 ,∴
,∴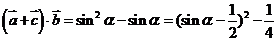
又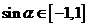 ,∴
,∴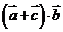 的取值范围为
的取值范围为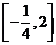 .
.
10 (温州市十校2008学年高三第一学期期初联考 数学试题(文)) .已知A、B、C三点的坐标分别为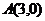 、
、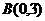 、
、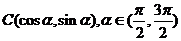 .
.
(1)若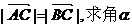 的值;
的值;
(2)若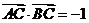 ,求
,求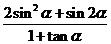 的值.
的值.
[解析](1) 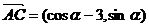
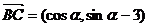
∵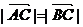 ∴
∴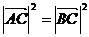
即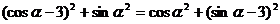
∴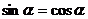 ,又∵
,又∵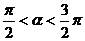 ,∴
,∴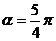 .
.
(2)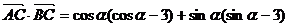
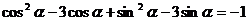 ,∴
,∴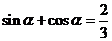 ,
,
两边平方,得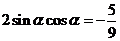 ,
,
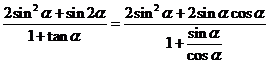
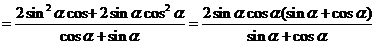
=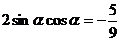 .
.
1(2008年安徽卷3).在平行四边形ABCD中,AC为一条对角线,若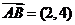 ,
,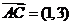 ,则
,则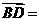 ( )
( )
A.(-2,-4) B.(-3,-5) C.(3,5) D.(2,4)
[解析]因为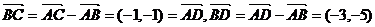 ,选B.
,选B.
[答案]B.
2(2007年山东文5).已知向量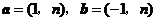 ,若
,若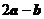 与
与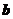 垂直,则
垂直,则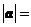 ( C )
( C )
A.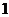 B.
B.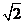 C.
C.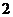 D.4
D.4
[解析]∵2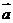 -
-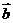 与
与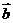 垂直. ∴(2
垂直. ∴(2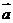 -
-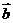 )·
)·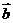 =0, 而2
=0, 而2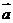 -
-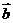 = (3 , n) , ∴-3+n2=0
, 而|
= (3 , n) , ∴-3+n2=0
, 而|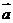 |2
=
|2
=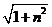 =
4 即 |
=
4 即 |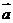 |=2
. 两个非零向量
|=2
. 两个非零向量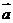 ⊥
⊥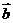

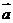 ·
·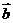 =0
=0 x1x2+y1y2=0
, |
x1x2+y1y2=0
, |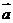 |2
=
|2
=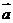 2
= x2 +y2.
2
= x2 +y2.
[答案]C.
3(2008年辽宁卷理5).已知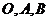 是平面上的三个点,直线
是平面上的三个点,直线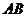 上有一点
上有一点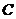 ,满足
,满足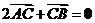 ,则
,则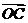 等于( )
等于( )
A.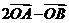 B.
B.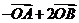 C.
C.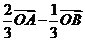 D.
D.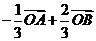
[解析]依题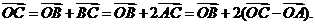 ∴
∴
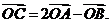
[答案]A.
4(2008年浙江卷理9).已知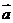 ,
,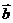 是平面内两个互相垂直的单位向量,若向量
是平面内两个互相垂直的单位向量,若向量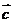 满足
满足 ,则
,则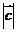 的最大值是( )
的最大值是( )
A. 1 B. 2 C. 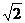 D.
D. 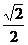
[解析]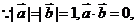
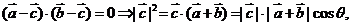
∴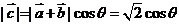 ,则
,则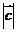 的最大值是
的最大值是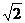 ;
;
∴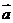 ,
,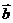 对应的点A,B在圆
对应的点A,B在圆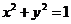 上,
上,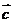 对应的点C在圆
对应的点C在圆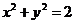 上即可.
上即可.
[答案]C.
5(2008年天津卷理14).如图,在平行四边形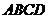 中,
中,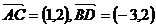 ,
,
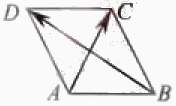 则
则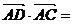 .
.
[解析]令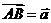 ,
,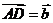 ,则
,则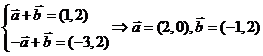
所以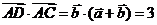 .
.
[答案]3.
6(2007年天津理15)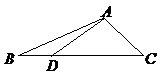 .如图,在
.如图,在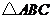 中,
中,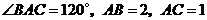 ,
,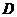 是边
是边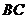 上一点,
上一点,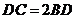 ,则
,则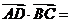 .
.
[解析]在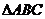 中,有余弦定理得
中,有余弦定理得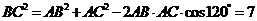 ,
,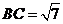 ,
,
由正弦定理得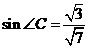 ,则
,则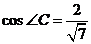 ,在
,在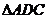 中,由余弦定理求得
中,由余弦定理求得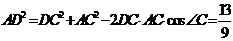 ,则
,则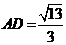 ,
,
由余弦定理得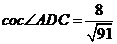 ,
,
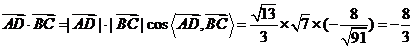 .
.
[答案] .
.
7(2007年广东文16).已知ΔABC三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(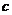 ,0).
,0).
(1)若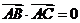 ,求
,求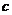 的值;
的值;
(2)若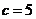 ,求sin∠A的值
,求sin∠A的值
[解析] (1) 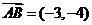 ,
,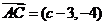 ,
,
由 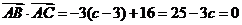 得
得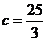 .
.
(2) 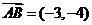 ,
,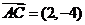 ,
,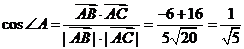 ,
,
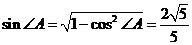 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com