
经历用向量的数量积推导出两角差的余弦公式的过程,进一步体会向量方法的作用,由此出发,导出其他的三角恒等变换公式,并能运用这些公式进行简单的恒等变换,从而发展学生的推理能力和运算能力.
1.和与差的三角函数公式
(1)向量的数量积推导出两角差的余弦公式.
(2)用两角差的余弦公式导出两角差的正弦、正切公式.
(3)用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系.
(4)体会化归思想的应用,能运用它们进行简单的三角函数式的化简、求值及恒等式的证明。
2、解答题
(1)解析几何章节内知识综合问题
已知向量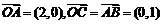 ,动点M到定直线
,动点M到定直线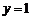 的距离等于
的距离等于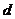 ,并且满足
,并且满足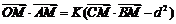 ,其中O为坐标原点,K为参数;
,其中O为坐标原点,K为参数;
(1)求动点M的轨迹方程,并判断曲线类型;
(2)当k=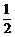 时,求
时,求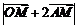 的最大值和最小值;
的最大值和最小值;
(3)在(2)的条件下,将曲线向左平移一个单位,在x轴上是否存在一点P(m,0)使得过点P的直线交该曲线于D、E两点、并且以DE为直径的圆经过原点,若存在,请求出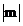 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
解题过程: (1)设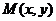 ,则由
,则由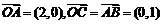 ,
,
且O为原点得A(2,0),B(2,1),C(0,1)
从而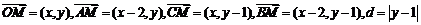
代入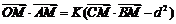 得
得
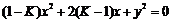 为所求轨迹方程
为所求轨迹方程
当K=1时,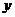 =0 轨迹为一条直线
=0 轨迹为一条直线
当K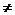 1时,
1时,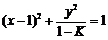 ,若K=0,则为圆 ;若K
,若K=0,则为圆 ;若K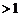 ,则为双曲线
,则为双曲线
(2)当K=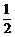 时,若
时,若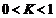 或
或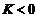 则为椭圆
则为椭圆
方程为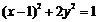 ,即
,即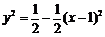 且
且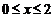
从而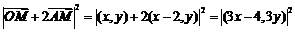
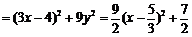
又 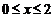
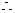 当
当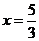 时,
时,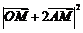 取最小值
取最小值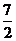 ,当
,当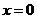 时,
时,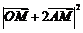 取最大值16
取最大值16
故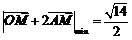 ,
,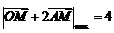
(3)在(2)的条件下,将曲线向左平移一个单位后曲线方程为 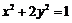
假设存在过P(m,0)直线满足题意条件,不妨设过P(m,0)直线方程为
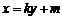
设D(x1,y1 ),E(x2,y2
),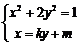 消去x得:
消去x得: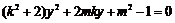
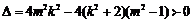 即
即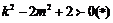
由韦达定理,得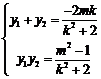
由于以DE为直径的圆都过原点则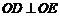 ,即
,即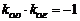
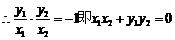
又因为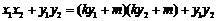
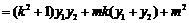
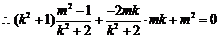 即
即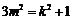 显然能满足
显然能满足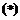
故当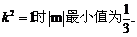
命题意图:解析几何大题在高考中以直线与圆锥曲线相交为背景,结合向量(向量起“表达”作用),考查求方程、最值、点的定位等问题。本题就是抓住这一特点进行命题的。另外特别说一下,09安徽高考数学解析几何大题要以椭圆为背景命题。
(2)解几与函数导数综合问题
已知圆O的方程为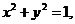 过直线
过直线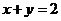 上的任意一点P作圆O的切线PA、PB.四边形OABP的面积取得最小时的点P的坐标(m,n)设
上的任意一点P作圆O的切线PA、PB.四边形OABP的面积取得最小时的点P的坐标(m,n)设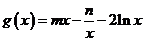 .
.
(1)求证:当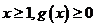 恒成立;
恒成立;
(2)讨论关于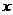 的方程:
的方程: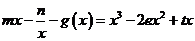 根的个数.
根的个数.
解题过程:(1)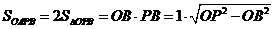 =
=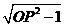 .
.
当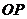 取得最小值时
取得最小值时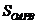 取得最小,过点O 作
取得最小,过点O 作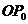 垂直于直线
垂直于直线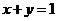 ,交点为
,交点为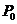 ,
,
易得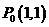 ,∴
,∴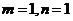 .∴
.∴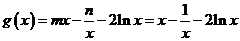 .
.
∴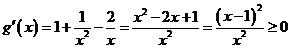 ,∴
,∴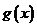 在
在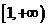 是单调增函数,
是单调增函数,
∴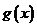
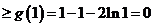 对于
对于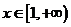 恒成立.
恒成立.
(2)方程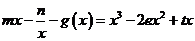 ,∴
,∴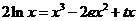 .
.
∵ 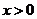 ,∴
方程为
,∴
方程为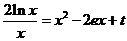 .令
.令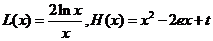 ,
,
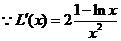 ,当
,当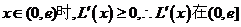 上为增函数;
上为增函数;
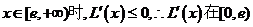 上为减函数,
上为减函数,
当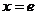 时,
时,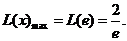
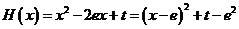 ,
,
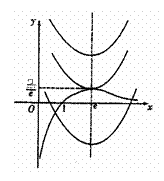
∴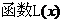 、
、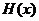 在同一坐标系的大致图象如图所示,
在同一坐标系的大致图象如图所示,
∴①当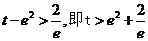 时,方程无解.
时,方程无解.
②当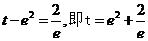 时,方程有一个根.
时,方程有一个根.
③当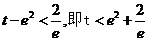 时,方程有两个根.
时,方程有两个根.
命题意图:解几大题在高考中以解几章节内部知识综合题为主,只有理科卷在高考中偶尔会有与导数函数综合型的问题。本题就在这一点上立意命题。
1、已知集合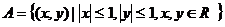 ,
,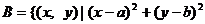
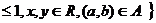 ,则集合
,则集合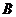 所表示图形的面积是
.
所表示图形的面积是
.
答案: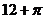
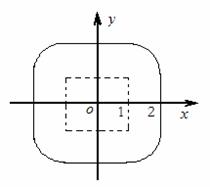 解题过程:集合
解题过程:集合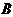 表示以
表示以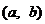 为圆心,1为半径的圆及内部的平面区域,其中圆心
为圆心,1为半径的圆及内部的平面区域,其中圆心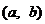 在边长为2的正方形区域
在边长为2的正方形区域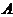 内移动(如图),故
内移动(如图),故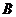 所表示的图形是“圆角”正方形,面积为:
所表示的图形是“圆角”正方形,面积为:
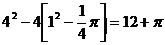 .
.
命题意图:主要考查学生对集合语言的理解以及对解几初步知识的运用能力,以线性规划求面积问题的面目出现,考察了直线、圆及点集的表示。
(2)参数方程与普通方程问题(理)(09年安徽文科不作为考试内容)
曲线的参数方程为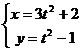 (t是参数),则曲线是( )
(t是参数),则曲线是( )
A、线段 B、双曲线的一支 C、圆 D、射线
解题过程:消去参数可得D选项
命题意图:参数方程在高考中只要求学生能化为普通方程即可。
(3)求参数的值问题(以圆锥曲线的离心率问题为主,对大题考不到的圆锥曲线做以补充)
几何参量
若抛物线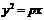 的焦点与椭圆
的焦点与椭圆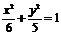 的右焦点重合,则
的右焦点重合,则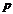 的值为( )
的值为( )
A.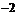 B. C.
B. C.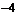 D.
D.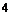
解题过程:椭圆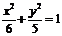 的右焦点为(1,0),所以抛物线
的右焦点为(1,0),所以抛物线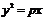 的焦点为(1,0),则
的焦点为(1,0),则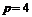 ,故选D.
,故选D.
命题意图: 本题主要考查抛物线、椭圆的标准方程和抛物线、椭圆的基本几何性质.
曲线的离心率
(1)椭圆的离心率e=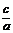 ∈(0,1) (e越大则椭圆越扁);
∈(0,1) (e越大则椭圆越扁);
(2) 双曲线的离心率e=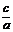 ∈(1, +∞) (e越大则双曲线开口越大).
∈(1, +∞) (e越大则双曲线开口越大).
已知双曲线的方程为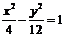 ,则双曲线的交点坐标为( ),离心率为( )
,则双曲线的交点坐标为( ),离心率为( )
解答过程: 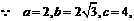 所以焦点是
所以焦点是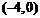 ,
,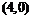 ,离心率为2
,离心率为2
命题意图:本题主要考查双曲线的标准方程和双曲线的离心率以及焦点等基本概念.
小结: 对双曲线的标准方程和双曲线的离心率以及焦点等基本概念,要注意认真掌握.尤其对双曲线的焦点位置和双曲线标准方程中分母大小关系要认真体会.
(2)极坐标与直角坐标的互化问题(理)(09年安徽文科不作为考试内容)
已知曲线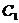 的极坐标方程为
的极坐标方程为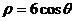 ,曲线
,曲线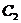 的极坐标方程为
的极坐标方程为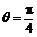 ,曲线
,曲线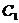 ,
,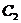 相交于
相交于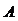 ,
,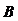 两点.
两点.
(Ⅰ)把曲线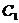 ,
,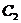 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
(Ⅱ)求弦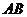 的长度.
的长度.
解题过程:(Ⅰ)曲线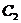 :
: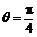 (
(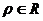 )表示直线
)表示直线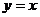 .曲线
.曲线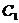 :
: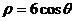 ,
,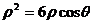 ,
,
所以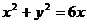 ,即
,即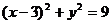 .
.
(Ⅱ)圆心(3,0)到直线的距离
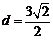 ,
,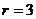 ,所以弦长
,所以弦长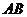 =
=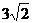 .
.
命题意图:极坐标在高考中的要求较低,只要能把极坐标与直角坐标进行互化即可。
1、小题(选择题、填空题)
(1) 线性规划问题
2、应试对策
(1)重视对教材中知识交汇点的复习。将解析几何与导数知识结合,利用导数求曲线的切线方程,建模后求参数的取值范围;将解析几何与向量结合,向量起“表达”或“工具”作用。所有这些都是高考命题的重点,因此对这类知识及问题要重视它的建模与解模的思想与方法,重视这些题型的训练。
(2)注重基础,掌握基本知识、基本方法、基本技能、基本内容。要多训练一些选择、填空题型。求直线、圆、圆锥曲线的方程,动点的轨迹,参数的范围以及对称问题等是高考考试中的重点题型,要熟练掌握求轨迹方程的方法与步骤,要熟练掌握求参数的范围的常用方法,考前要对这些重要内容与重要方法,进行一定量的适应性训练,使之成为技能,成为常法,考时才能得心应手。
(3)重视圆锥曲线的定义在解题中的应用。有关圆锥曲线上的点到焦点的距离,曲线上的点到准线的距离,离心率的问题等都可用圆锥曲线的定义去求解,活用定义,可以大大缩短破题与解题的时间,减少运算量,进而大大提高自己的解题自信心。
(4)熟练掌握坐标法的思想。要注意学习如何借助于坐标系,用代数的方法来研究几何问题,体会这种数形结合的思想的应用;要会寻找点与坐标的对应关系、曲线与方程的对应关系,把几何问题转化为代数问题。这儿顺便提一下:有关圆的问题,解答时一定要充分利用圆的几何性质,如圆与直线相切、相交的性质,圆与圆的位置关系,这样可以大大减少运算量,并使过程得以简化。
1。命题预测
直线与圆是最基本的图形,是解析几何的基本内容,也是高考必考查的内容,试题多为选择和填空题,难度适中,属基本要求,但偶有与圆有关问题的解答题,其解答难度则可能较大。试题常在直线的图象、求直线方程,直线 的平行与垂直的位置关系,求圆面积的方程与有关圆的轨迹问题上作重点考查。同时有关对称问题也是高考的热点问题,其中直线与圆的位置关系与对称问题出现频率较高。而随着平面向量的出现,向量与直线或圆的综合问题则是一直高考的新热点。
圆锥曲线是平面解析几何的核心内容,因而是高考考查的重点内容。在每年的高考中一般有两道选择或填空题以及一道解答题。两道小题目通常是一道较易的“低档”题与一道“中档”题,主要考查圆锥曲线的标准方程及其几何性质等基础知识、基本技能以及基本方法的灵活运用,特别是要注意离心率的考察。而解答题则是注重对数学思想方法和数学语言的考查,重视对圆锥曲线定义的应用的考查。求轨迹以及直线与圆锥曲线的位置关系的考题,将注重考查与一元二次方程有关的判别式、韦达定理等腰三角形的应用。
4、(2008学年度第一学期上海市普陀区高三年级质量调研第16题)(本题满分12分)设点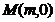 在椭圆
在椭圆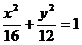 的长轴上,点
的长轴上,点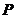 是椭圆上任意一点. 当
是椭圆上任意一点. 当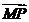 的模最小时,点
的模最小时,点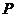 恰好落在椭圆的右顶点,求实数
恰好落在椭圆的右顶点,求实数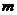 的取值范围.
的取值范围.
答案:解:设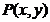 为椭圆上的动点,由于椭圆方程为
为椭圆上的动点,由于椭圆方程为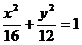 ,故
,故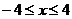 .
.
因为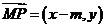 ,所以
,所以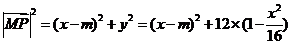
推出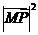
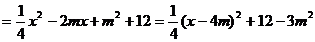 .
.
依题意可知,当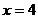 时,
时,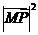 取得最小值.而
取得最小值.而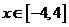 ,
,
故有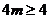 ,解得
,解得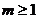 .
.
又点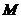 在椭圆的长轴上,即
在椭圆的长轴上,即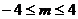 . 故实数
. 故实数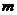 的取值范围是
的取值范围是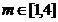 .
.
[点评]与圆锥曲线有关的最值问题、参数范围问题综合性较强,解题时需根据具体问题灵活的运用平面几何、函数、不等式等知识,正确的构造出圆锥曲线与其他数学知识的联系。
3、(金丽衢十二校高三第一次联考数学试卷(理科))
已知椭圆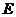 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过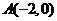 、
、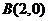 、
、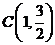 三点.
三点.
(1)求椭圆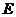 的方程:
的方程:
(2)若点D为椭圆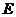 上不同于
上不同于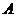 、
、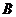 的任意一点,
的任意一点,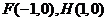 ,当
,当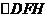 内切圆的面积最大时。求内切圆圆心的坐标;
内切圆的面积最大时。求内切圆圆心的坐标;
(3)若直线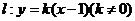 与椭圆
与椭圆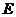 交于
交于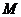 、
、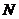 两点,证明直线
两点,证明直线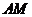 与直线
与直线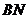 的交点在直线
的交点在直线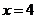 上.
上.
[解析](1)设椭圆方程为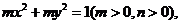
将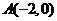 、
、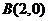 、
、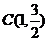 代入椭圆E的方程,得
代入椭圆E的方程,得
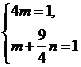 解得
解得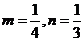 .
.
∴椭圆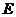 的方程
的方程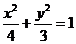 (4分)
(4分)
(2)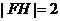 ,设
,设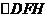 边上的高为
边上的高为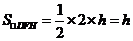
当点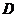 在椭圆的上顶点时,
在椭圆的上顶点时,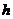 最大为
最大为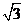 ,所以
,所以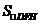 的最大值为
的最大值为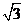 .
.
设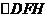 的内切圆的半径为
的内切圆的半径为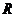 ,因为
,因为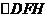 的周长为定值6.所以
的周长为定值6.所以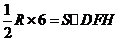 ,
,
所以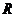 的最大值为
的最大值为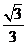 .所以内切圆圆心的坐标为
.所以内切圆圆心的坐标为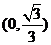 (10分)
(10分)
(3)法一:将直线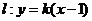 代入椭圆
代入椭圆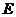 的方程
的方程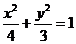 并整理.
并整理.
得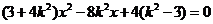 .
.
设直线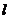 与椭圆
与椭圆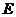 的交点
的交点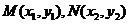 ,
,
由根系数的关系,得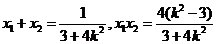 .
.
直线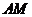 的方程为:
的方程为: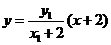 ,它与直线
,它与直线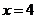 的交点坐标为
的交点坐标为
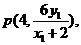 同理可求得直线
同理可求得直线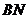 与直线
与直线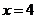 的交点坐标为
的交点坐标为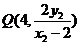 .
.
下面证明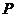 、
、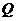 两点重合,即证明
两点重合,即证明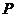 、
、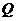 两点的纵坐标相等:
两点的纵坐标相等:
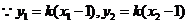 ,
,
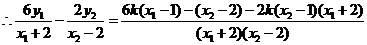
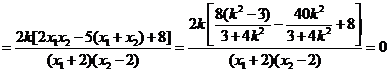
因此结论成立.
综上可知.直线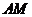 与直线
与直线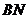 的交点住直线
的交点住直线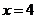 上. (16分)
上. (16分)
法二:直线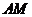 的方程为:
的方程为: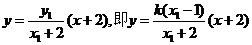
由直线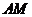 的方程为:
的方程为: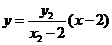 ,即
,即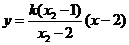
由直线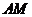 与直线
与直线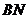 的方程消去
的方程消去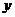 ,得
,得
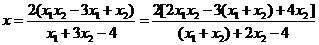
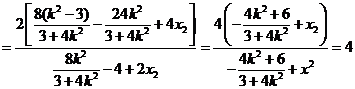
∴直线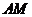 与直线
与直线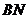 的交点在直线
的交点在直线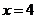 上.
上.
[点评]本题是将直线、圆与椭圆结合运用方程思想解题。
2、(辽宁省部分重点中学协作体2008年高考模拟)
在正△ABC中,D∈AB,E∈AC,向量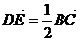 ,则以B,C为焦点,且过D,E的双曲线的离心率为 ( )
,则以B,C为焦点,且过D,E的双曲线的离心率为 ( )
A.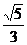 B.
B.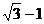 C.
C.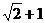 D.
D.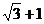
[解析]D.
[点评]由几何图形的性质得到关于a,b,c的齐次等式
1.(辽宁省沈阳二中2008-2009学年上学期高三期中考试)
直线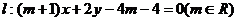 恒过定点C,圆C是以点C为圆心,以4为半径的圆。
恒过定点C,圆C是以点C为圆心,以4为半径的圆。
(1)求圆C的方程;
(2)设圆M的方程为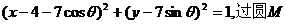 上任意一点P分别作圆C的两条切线PE、PF,切点为E、F,求
上任意一点P分别作圆C的两条切线PE、PF,切点为E、F,求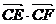 的最大值和最小值。
的最大值和最小值。
[解析](1)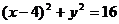 ,
,
(2)设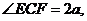 则
则
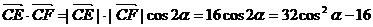
在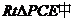 ,
,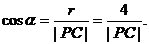
由圆的几何性质得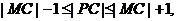
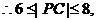
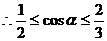 ,由此可得
,由此可得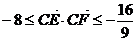
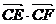 的最大值为-
的最大值为-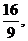 最小值为-8
最小值为-8
[点评]向量与解析几何结合是高考命题的重要趋势,本题难度不大。但是如果不能将“向量语言”准确转化为“函数语言”,或在解题中不细心都可能会出现错误。切记:“细节决定成败”
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com