
6. 已知函数f(x) = 2x2-x,则使得数列{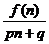 }(n∈N+)成等差数列的非零常数p与q所满足的关系式为 .p=-2q
}(n∈N+)成等差数列的非零常数p与q所满足的关系式为 .p=-2q
5. 一个机器猫每秒前进或后退一步,程序设计人员让机器猫以每前进3步,然后再后退2步的规律移动;如果将此机器猫放在数轴的原点上,面向正的方向,以1步的距离为1个单位长,令P(n)表示第n秒时机器猫所在的位置的坐标,且P(0)=0,那么下列结论中错误的是( C)
(A)P(3)=3 (B)P(5)=1 (C)P(101)=21 (D)P(103)<P(104)
4. 弹子棋共有60颗大小相同的球形弹子,现在棋盘上将它叠成正四面体形的球垛,使剩下的弹子尽可能少,那么剩余的弹子有(B)
(A)0颗 (B)4颗 (C)5颗 (D)11颗
3. 若数列{an}满足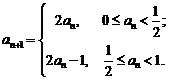 若
若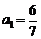 ,则
,则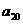 的值为( B )
的值为( B )
(A) 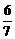 (B)
(B) 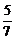 (C)
(C) 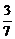 (D)
(D)
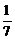
2. 数学拓展课上,老师定义了一种运算“*”,对于n∈N*满足以下运算性质:
(1) 2*2 = 1,(2) ( 2n + 2) * 2 = 3(2n * 2).则2n*2用含n的代数式表示为 3n-1_
1. 设数列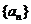 的前n项和为
的前n项和为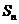 ,令
,令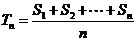 ,称
,称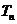 为数列
为数列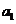 ,
,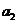 ,…,
,…,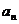 的“理想数”,已知数列
的“理想数”,已知数列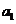 ,
,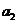 ,…,
,…,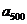 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 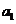 ,
,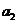 ,……,
,……,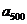 的“理想数”为(A)
的“理想数”为(A)
(A) 2002 (B) 2004 (C) 2006 (D) 2008
6.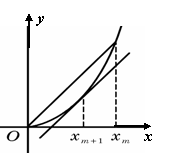 已知函数f (x)=
已知函数f (x)=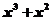 ,数列|x
,数列|x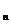 |(x
|(x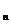 >0)的第一项x
>0)的第一项x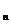 =1,以后各项按如下方式取定:曲线x=f (x)在
=1,以后各项按如下方式取定:曲线x=f (x)在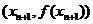 处的切线与
处的切线与
经过(0,0)和(x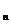 ,f (x
,f (x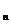 ))两点的直线平行(如图).
))两点的直线平行(如图).
求证:当n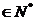 时,
时,
(Ⅰ) x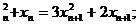
(Ⅱ)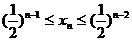 .
.
[专家解答](I ) 证明:因为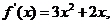
所以曲线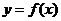 在
在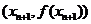 处的切线斜率
处的切线斜率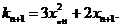
即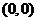 和
和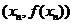 两点的直线斜率是
两点的直线斜率是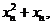 以
以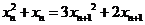 .
.
(II)因为函数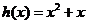 ,当
,当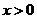 时单调递增,
时单调递增,
而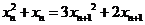
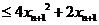
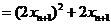 ,
,
所以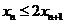 ,即
,即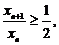 因此
因此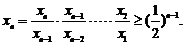
又因为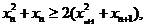 令
令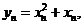 则
则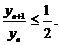
因为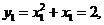 所以
所以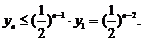
因此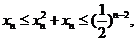 故
故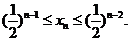
★★★高考要考什么
[考点透视]
本专题是等差(比)数列知识的综合应用,同时加强数学思想方法的应用,是历年的重点内容之一,近几年考查的力度有所增加,体现高考是以能力立意命题的原则.
[热点透析]
高考中常常把数列、极限与函数、方程、不等式、解析几何等等相关内容综合在
一起,再加以导数和向量等新增内容,使数列综合题新意层出不穷.常见题型:
(1)由递推公式给出数列,与其他知识交汇,考查运用递推公式进行恒等变形、
推理与综合能力.
(2)给出Sn与an的关系,求通项等,考查等价转化的数学思想与解决问题能力.
(3)以函数、解析几何的知识为载体,或定义新数列,考查在新情境下知识的迁移能力.
理科生需要注意数学归纳法在数列综合题中的应用,注意不等式型的递推数列.
★★★突破重难点
[范例1]已知数列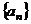 中,对一切自然数
中,对一切自然数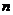 ,都有
,都有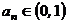 且
且
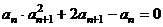 .
.
求证:(1)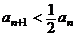 ;
;
(2)若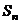 表示数列
表示数列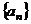 的前
的前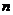 项之和,则
项之和,则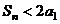 .
.
解析: (1)由已知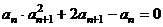 得
得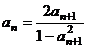 ,
,
又因为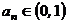 ,所以
,所以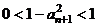 , 因此
, 因此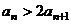 ,即
,即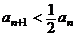 .
.
(2) 由结论(1)可知 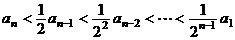 ,即
,即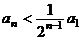 ,
,
于是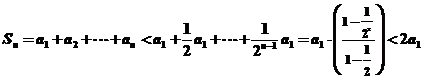 ,
,
即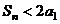 .
.
[点睛]从题目的结构可以看出,条件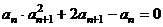 是解决问题的关键,必须从中找出
是解决问题的关键,必须从中找出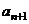 和
和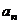 的关系.
的关系.
[文]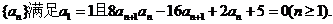 记
记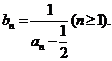
(Ⅰ)求b1、b2、b3、b4的值;
(Ⅱ)求数列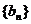 的通项公式及数列
的通项公式及数列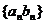 的前n项和
的前n项和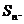
解析(I)
整理得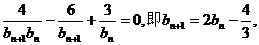
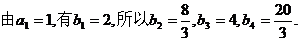
(Ⅱ)由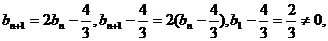
所以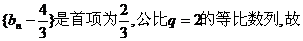
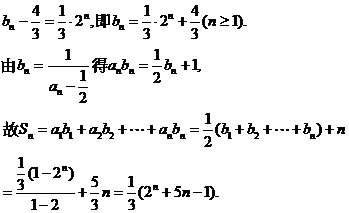
[范例2]设数列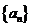 的前
的前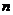 项的和
项的和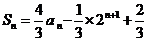 ,
,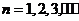
(Ⅰ)求首项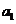 与通项
与通项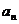 ;
;
(Ⅱ)设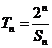 ,
,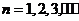 ,证明:
,证明: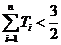
解析 (Ⅰ)由 Sn=an-×2n+1+, n=1,2,3,… ①
得 a1=S1= a1-×4+ 所以a1=2.
再由①有 Sn-1=an-1-×2n+, n=2,3,4,…
将①和②相减得: an=Sn-Sn-1= (an-an-1)-×(2n+1-2n), n=2,3, …
整理得: an+2n=4(an-1+2n-1),n=2,3, …, 因而数列{an+2n}是首项为a1+2=4,公比为4的等比数列,即an+2n = 4×4 n-1= 4 n, n=1,2,3, …, 因而an=4n-2n, n=1,2,3, …
(Ⅱ) Sn= ×(4n-2n)-×2n+1 + = ×(2n+1-1)(2n+1-2) = ×(2n+1-1)(2n-1)
Tn= = × = ×( - )
所以 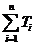 =
= 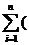 - ) = ×( - ) <
- ) = ×( - ) <
[点睛]Sn与an始终是我们的重点,需要我们引起重视;注意总结积累数列不等式放缩的技巧.
[文]设数列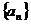 的前n项和为Sn,若
的前n项和为Sn,若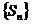 是首项为S1各项均为正数且公比为q的等比数列.
是首项为S1各项均为正数且公比为q的等比数列.
(1)求数列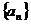 的通项公式
的通项公式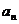 (用S1和q表示);
(用S1和q表示);
(2)试比较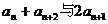 的大小,并证明你的结论.
的大小,并证明你的结论.
解析 (1)∵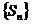 是各项均为正数的等比数列, ∴
是各项均为正数的等比数列, ∴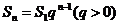 .
.
当n=1时,a1=S1; 当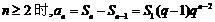 .
.
∴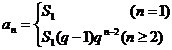
(2)当n=1时,
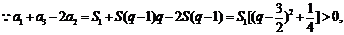 ∴
∴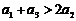 .
.
当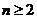 时,
时,
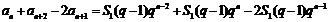
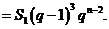
∵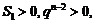
①当q=1时,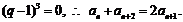
②当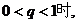
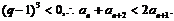
③当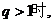
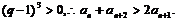
综上可知:当n=1时,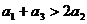 .当
.当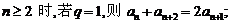
若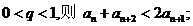 若
若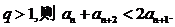
[范例3]由坐标原点O向曲线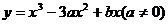 引切线,切于O以外的点P1
引切线,切于O以外的点P1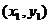 ,再由P1引此曲线的切线,切于P1以外的点P2
,再由P1引此曲线的切线,切于P1以外的点P2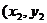 ),如此进行下去,得到点列{ Pn
),如此进行下去,得到点列{ Pn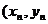 }}.
}}.
求:(Ⅰ)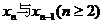 的关系式;
的关系式;
(Ⅱ)数列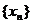 的通项公式;
的通项公式;
(Ⅲ)当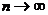 时,
时,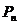 的极限位置的坐
的极限位置的坐
解析 (Ⅰ)由题得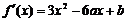
过点P1(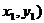 的切线为
的切线为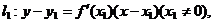
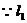 过原点
过原点 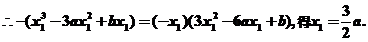
又过点Pn(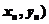 的
的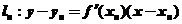
因为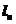 过点Pn-1(
过点Pn-1(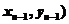
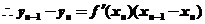
整理得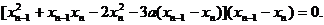
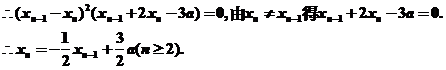
(Ⅱ)由(I)得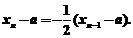
所以数列{xn-a}是以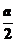 公比为
公比为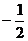 的等比数列
的等比数列
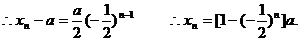
(法2)通过计算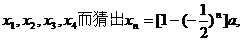 再用数学归纳法证明.
再用数学归纳法证明.
(Ⅲ)
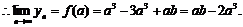
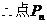 的极限位置为(
的极限位置为(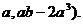
[点睛]注意曲线的切线方程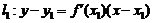 的应用,从而得出递推式.
的应用,从而得出递推式.
[文]数列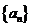 的前
的前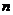 项和为
项和为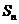 ,已知
,已知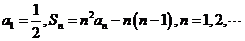
(Ⅰ)写出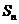 与
与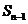 的递推关系式
的递推关系式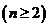 ,并求
,并求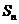 关于
关于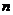 的表达式;
的表达式;
(Ⅱ)设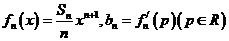 ,求数列
,求数列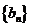 的前
的前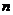 项和
项和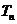 .
.
解析 由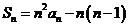
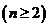 得
得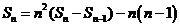 ,
,
即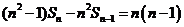 ,所以
,所以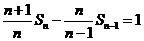 ,对
,对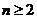 成立.
成立.
由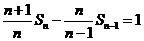 ,
,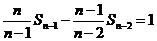 ,…,
,…,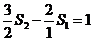
相加得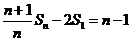 ,又
,又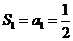 ,所以
,所以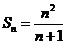 ,
,
当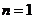 时,也成立.
时,也成立.
(Ⅱ)由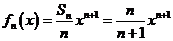 ,得
,得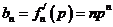 .
.
而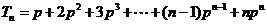 ,
,
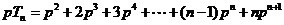 ,
,
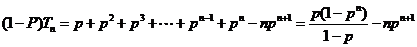 .
.
[范例4]设点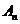 (
(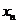 ,0),
,0),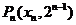 和抛物线
和抛物线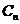 :y=x2+an
x+bn(n∈N*),其中an=-2-4n-
:y=x2+an
x+bn(n∈N*),其中an=-2-4n-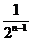 ,
,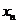 由以下方法得到:
由以下方法得到:
x1=1,点P2 (x2,2)在抛物线C1:y=x2+a1x+b1上,点A1(x1,0)到P2的距离是A1到C1上点的最短距离,…,点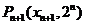 在抛物线
在抛物线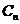 :y=x2+an
x+bn上,点
:y=x2+an
x+bn上,点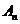 (
(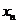 ,0)到
,0)到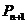 的距离是
的距离是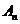 到
到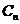 上点的最短距离.
上点的最短距离.
(Ⅰ)求x2及C1的方程.
(Ⅱ)证明{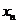 }是等差数列.
}是等差数列.
解:(Ⅰ)由题意,得A(1,0), C1:y=x2-7x+b1.
设点P(x,y)是C1上任意一点,则|A1P|=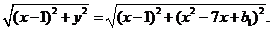
令f (x)=(x-1)2+(x2-7x+b1)2,
则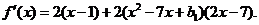
由题意得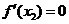 , 即
, 即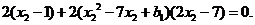
又P2(x2,0)在C1上, ∴2=x22 -7x2+b1
解得x2=3, b1=14. 故C1方程为y=x2-7x+14.
(Ⅱ)设P(x,y)是C1上任意一点,则
|AnP|=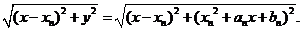
令g(x)=(x-xn)2+(x2+anx+bn)2,则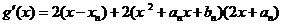 ,
,
由题意得,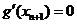 ,即
,即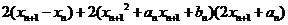 =0,
=0,
又∵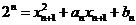 ,∴(xn+1-xn)+2n(2xn+1+an)=0(n≥1),
,∴(xn+1-xn)+2n(2xn+1+an)=0(n≥1),
即(1+2n+1)xn+1- xn+2 n an =0, (*)
下面用数学归纳法证明xn=2n-1.
① 当n=1时,x1=1,等式成立.
② 假设当n=k时,等式成立,即xk=2k-1.
则当n=k+1时,由(*)知(1+2k+1)xk+1-xk+2kak=0, (*)
又ak=-2-4k-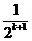 ,∴
,∴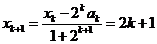 .
.
即当n=k+1,时等式成立.
由①②知,等式对n∈N+成立,∴{xn}是等差数列.
[点睛]注意第(1)小题其实是第(2)小题的特例,对于求数列的通项公式,归纳猜想证明是十分常用的手段.
[文]已知数列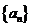 满足
满足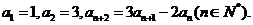
(I)证明:数列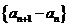 是等比数列;
是等比数列;
(II)求数列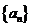 的通项公式;
的通项公式;
(II)若数列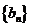 满足
满足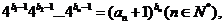 证明
证明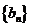 是等差数列.
是等差数列.
解析 (I)证明: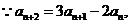
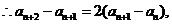
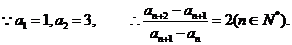
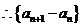 是以
是以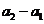
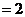 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
(II)解:由(I)得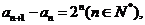
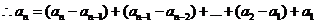
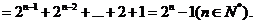
(III)证明: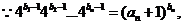
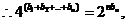
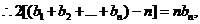 ①
①
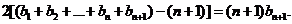 ②
②
②-①,得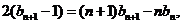
即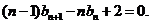 ③
③
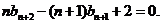 ④
④
④-③,得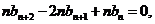 即
即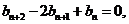
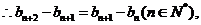
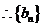 是等差数列.
是等差数列.
★★★自我提升
5.已知n次式项式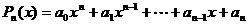 .
.
若在一种算法中,计算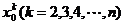 的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),则计算P10(x0)的值共需要 65 次运算.
的值需要k-1次乘法,计算P3(x0)的值共需要9次运算(6次乘法,3次加法),则计算P10(x0)的值共需要 65 次运算.
下面给出一种减少运算次数的算法:P0(x)=a0,Pk+1(x)=xPk(x)+ak+1(k=0,1,2,…,n-1).利用该算法,计算P3(x0)的值共需要6次运算,计算Pn(x0)的值共需要 2n 次运算.
4.对正整数n,设曲线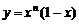 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为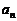 ,则数列
,则数列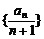 的前n项和的公式是 2n+1-2
.
的前n项和的公式是 2n+1-2
.
3.在数列{an}中,若a1=1,an+1=2an+3 (n≥1),则该数列的通项an=__2 n+1-3___.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com