
1.作者简介:巴尔扎克(1799-1850)是19世纪法国伟大的批判现实主义作家,欧洲批判现实主义文学的奠基人和杰出代表。巴尔扎克出生于一个法国大革命后致富的资产阶级家庭,法科学校毕业后,拒绝家庭为他选择的受人尊敬的法律职业,而立志当文学家。为了获得独立生活和从事创作的物质保障,他曾试笔并插足商业,从事出版印刷业,但都以破产告终。这一切都为他认识社会、描写社会提供了极为珍贵的第一手材料。他不断追求和探索,对哲学、经济学、历史、自然科学、神学等领域进行了深入研究,积累了极为广博的知识。
1829年,巴尔扎克完成长篇小说《朱安党人》,这部取材于现实生活的作品为他带来巨大声誉,也为法国批判现实主义文学放下第一块基石,巴尔扎克将《朱安党人》和计划要写的一百四五十部小说总命名为《人间喜剧》,并为之写了《前言》,阐述了他的现实主义创作方法和基本原则,从理论上为法国批判现实主义文学奠定了基础。
巴尔扎克一生创作96部长、中、短篇小说和随笔,总名为《人间喜剧》。这是一部“社会百科全书”,展示了19世纪前半叶整个法国的社会生活画卷,真实地再现了贵族阶级的衰亡史及资产阶级的发家史,深刻地揭露了资本主义社会金钱主宰一切的特征。其中代表作为《欧也妮·葛朗台》、《高老头》。100多年来,他的作品传遍了全世界,对世界文学的发展和人类进步产生了巨大的影响。马克思、恩格斯称赞他“是超群的小说家”、“现实主义大师”。
巴尔扎克在艺术上取得巨大成就,他在小说结构方面匠心独运,小说结构多种多样,不拘一格、并善于将集中概括与精确描摹相结合,以外形反映内心本质等手法来塑造人物,他还善于以精细人微、生动逼真的环境描写再现时代风貌。恩格斯称赞巴尔扎克的《人间喜剧》写出了贵族阶级的没落衰败和资产阶级的上升发展,提供了社会各个领域无比丰富的生动细节和形象化的历史材料,“甚至在经济的细节方面(如革命以后动产和不动产的重新分配),我学到的东西也要比从当时所有职业历史学家、经济学院和统计学家那里学到的全部东西还要多”。(恩格斯:《恩格斯致玛·哈克奈斯》)巴尔扎克以自己的创作在世界文学史上树立起不朽的丰碑。
4.交流评价人物形象及小说主题。
文本导学
3.体会通过心理描写、语言描写展现人物性格的写法。
2.了解小说《高老头》的故事梗概及时代背景。
1.了解作者巴尔扎克及其作品。
1 证明下列不等式:
证明下列不等式:
(1)a,b∈R,求证|a+b|≤|a|+|b|;
(2)已知|h|<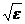 ,|k|<
,|k|<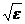 (ε>0),求证:|hk|<ε;
(ε>0),求证:|hk|<ε;
(3)已知|h|<cε, c <|x| (c>0,ε>0),求证:|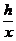 |<ε
|<ε
分析:用绝对值性质及不等式性质作推理运算 绝对值性质有:
绝对值性质有:
|ab|=|a|·|b|;|an|=|a|n,|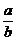 |=
|=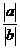 等
等
证明:(1)证法1:∵-|a|≤a≤|a|,-|b|≤b≤|b|
∴-(|a|+|b|)≤a+b≤|a|+|b| 即|a+b|≤|a|+|b|
证法2:(平方作差)(|a|+|b|)2-|a+b|2=a2+2|a||b|+b2-(a2+2ab+b2)
=2[|a|·|b|-ab)=2(|ab|-ab)≥0显然成立 故(|a|+|b|)2≥|a+b|2
故(|a|+|b|)2≥|a+b|2
又∵|a|+|b|≥0,|a+b|≥0,所以|a|+|b|≥|a+b|, 即|a+b|≤|a|+|b|
(2)∵0≤|h|<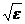 ,0≤|k|<
,0≤|k|<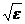 (ε>0),∴0≤|hk|=|h|·|k|<
(ε>0),∴0≤|hk|=|h|·|k|<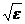 ·
·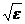 =ε
=ε
(3)由0<c<|x|可知:
0<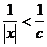 且0≤|h|<cε,∴
且0≤|h|<cε,∴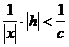 ·cε,即|
·cε,即|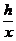 |<ε
|<ε
2 求证:|x+
求证:|x+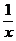 |≥2(x≠0)
|≥2(x≠0)
分析:x与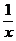 同号,因此有|x+
同号,因此有|x+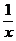 |=|x|+|
|=|x|+|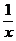 |
|
证法一:∵x与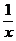 同号,∴|x+
同号,∴|x+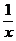 |=|x|+
|=|x|+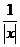
∴|x+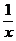 |=|x|+
|=|x|+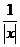 ≥2
≥2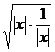 =2,即|x+
=2,即|x+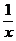 |≥2
|≥2
证法二:当x>0时,x+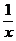 ≥2
≥2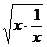 =2
=2
当x<0时,-x>0,有
-x+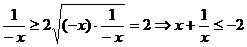
∴x∈R且x≠0时有x+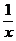 ≤-2,或x+
≤-2,或x+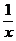 ≥2
≥2
即|x+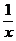 |≥2
|≥2
方法点拨:不少同学这样解:
因为|x+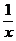 |≤|x|+
|≤|x|+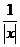 ,又|x|+
,又|x|+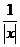 ≥2
≥2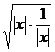 =2,所以|x+
=2,所以|x+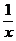 |≥2
|≥2
学生认为这样解答是根据不等式的传递性 实际上,上述两个不等式是异向不等式,是不符合传递性的,因而如此作解是错误的
实际上,上述两个不等式是异向不等式,是不符合传递性的,因而如此作解是错误的
3 已知:|A-a|<
已知:|A-a|<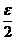 ,|B-b|<
,|B-b|<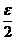 ,求证:
,求证:
(1)|(A+B)-(a+b)|<ε;(2)|(A-B)-(a-b)|<ε
分析:证明本题的关键是把结论的左边凑出条件的左边,创造利用条件的机会
证明:因为|A-a|<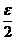 ,|B-b|<
,|B-b|<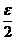

所以(1)|(A+B)-(a+b)|=|(A-a)+(B-b)|≤|A-a|+|B-b|<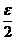 +
+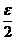 =ε
=ε
即|(A+B)-(a+b)|<ε
(2)|(A-B)-(a-b)|=|(A-a)-(B-b)|≤|A-a|+|B-b|<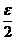 +
+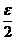 =ε
=ε
即|(A-B)-(a-b)|<ε
方法点拨:本题的证明过程中运用了凑的技巧,望给予足够重视,灵活掌握
已知:|x-1|≤1,
求证:(1)|2x+3|≤7; (2)|x2-1|≤3
证明:(1)∵|2x+3|=|2(x-1)+5|≤2|x-1|+5≤2+5=7
(2)|x2-1|=|(x+1)(x-1)|=|(x-1)[(x-1)+2]|
≤|x-1||(x-1)+2|≤|x-1|+2≤1+2=3
例1 已知|x|<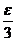 ,|y|<
,|y|<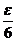 ,|z|<
,|z|<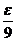 , 求证 |x+2y-3z|<ε
, 求证 |x+2y-3z|<ε
证明:|x+2y-3z|≤|x|+|2y|+|-3z|=|x|+2|y|+3|z|
∵|x|<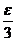 ,|y|<
,|y|<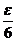 ,|z|<
,|z|<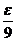 ,
,
∴|x|+2|y|+3|z|<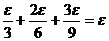
∴|x+2y-3z|<ε
说明:此例题主要应用了推论1,其中出现的字母ε,其目的是为学生以后学习微积分作点准备
例2 设a, b, c, d都是不等于0的实数,求证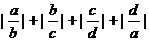 ≥4
≥4
证明:∵ 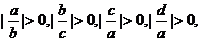
∴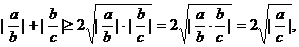 ①
①
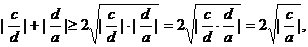 ②
②
又 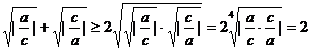 ③
③
由①,②,③式,得
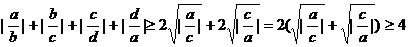
说明:此题作为一个含绝对值的不等式,在证明过程中运用了基本不等式及不等式的性质,在证法上采用的是综合法
例3
已知|a|<1,|b|<1,求证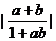 <1
<1
证明: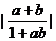 <1
<1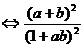 <1
<1
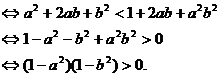
由|a|<1,|b|<1,可知(1-a2)(1-b2)>0成立,所以 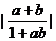 <1
<1
说明:此题运用了|x|<a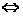 x2<a2这一等价条件将绝对值符号去掉,并采用了求差比较法证明其等价不等式的正确性,并用到了绝对值的有关性质,也体现了证明不等式的方法的综合性和灵活性
x2<a2这一等价条件将绝对值符号去掉,并采用了求差比较法证明其等价不等式的正确性,并用到了绝对值的有关性质,也体现了证明不等式的方法的综合性和灵活性
例4 设|a|<1, |b|<1 求证|a+b|+|a-b|<2
证明:当a+b与a-b同号时,|a+b|+|a-b|=|a+b+a-b|=2|a|<2
当a+b与a-b异号时,|a+b|+|a-b|=|a+b-(a-b)|=2|b|<2
∴|a+b|+|a-b|<2
例5 已知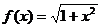 当a¹b时 求证:
当a¹b时 求证: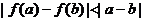
证法一: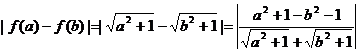
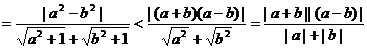
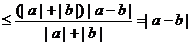
 证法二:(构造法)如图
证法二:(构造法)如图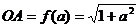 ,
,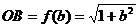
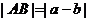 ,由三角形两边之差小于第三边得
,由三角形两边之差小于第三边得
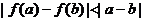
定理: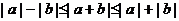
证明:∵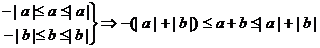
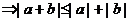 ①
①
又∵a=a+b-b |-b|=|b|
由①|a|=|a+b-b|≤|a+b|+|-b| 即|a|-|b|≤|a+b| ②
综合①②: 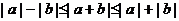
注意:1° 左边可以“加强”同样成立,即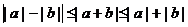
2° 这个不等式俗称“三角不等式”-三角形中两边之和大于第三边,两边之差小于第三边
3° a,b同号时右边取“=”,a,b异号时左边取“=”
推论1: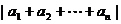 ≤
≤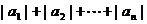
推论2: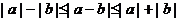
证明:在定理中以-b代b得: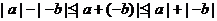
即 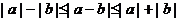
前面我们已学过不等式的性质和证明方法,这一节我们再来研究一些含有绝对值的不等式的证明问题
我们知道,当a>0时,
|x|<a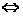 -a<x<a,
-a<x<a,
|x|>a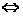 x>a或x<-a
x>a或x<-a
根据上面的结果和不等式的性质,我们可以推导出含有绝对值的不等式具有下面的性质
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com