4.(2008·北京理，5)若实数x，y满足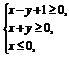则z=3^x+2y的最小值是　　　　　　　　　 (　　 )　

?A.0?　　　　　　　　　　 B.1　 ?　　　　　　　　 C.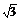?　　　　　　　　 D.9　

答案?B?　

3.若点(1，3)和(-4，-2)在直线2x+y+m=0的两侧，则m的取值范围是　　　　　 　 (　　 )　

? A.m<-5或m＞10　　　　　　　　　　　　　　　　　 B.m=-5或m=10　

? C.-5＜m＜10　　　　　　　　　　　　　　　　　　 D.-5≤m≤10　

答案?C?　

2.(2008·天津理，2)设变量x，y满足约束条件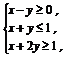则目标函数z=5x+y的最大值为(　　 )　

A.2　　 　　　　　　　 ?B.3?　　　　　　　　　　 C.4?　　　　　　　　　 D.5　

答案?D?　

1.已知点A(1，-1)，B(5，-3)，C(4，-5)，则表示△ABC的边界及其内部的约束条件是　　　　 .　

答案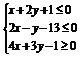　 　

12.已知直线l经过两条直线l₁:x+2y=0与l₂:3x-4y-10=0的交点，且与直线l₃:5x-2y+3=0的夹角为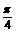,求直线l的方程.　

解 由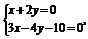

解得l₁和l₂的交点坐标为(2，-1).　

设所求直线l的方程为y+1=k(x-2).　

又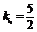,由l与l₃的夹角为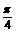

得tan=,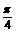　

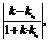即1=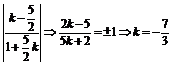或k=.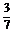　

故所求的直线l的方程为　

y+1=-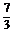(x-2)或y+1=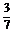(x-2),　

即7x+3y-11=0或3x-7y-13=0.

§7.3 简单的线性规划

基础自测

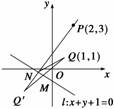
11.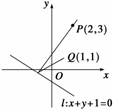一条光线经过P(2，3)点，射在直线l:x+y+1=0上，反射后穿过Q(1，1).

(1)求光线的入射方程；

(2)求这条光线从P到Q的长度.

解　 (1)设点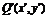为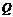关于直线l的对称点且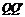交l于M点，∵k_l=-1，∴k_QQ′=1.

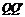∴所在直线方程为y-1=1·(x-1)

即x-y=0.

由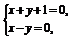

解得l与QQ′的交点M的坐标为.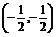

又∵M为QQ′的中点，

由此得.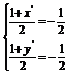

解之得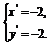∴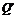(-2，-2).

设入射线与l交点N，且P，N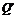，共线.

则P(2，3)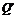，(-2，-2)，得入射线方程为

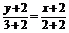，即5x-4y+2=0.

(2)∵l是QQ′的垂直平分线，因而|NQ|=.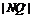

∴|PN|+|NQ|=|PN|+|NQ′|=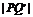

==,

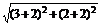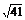即这条光线从P到Q的长度是.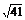

10.已知A(0，3)、B(-1，0)、C(3，0)，求D点的坐标，使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列).

解　 设所求点D的坐标为(x，y)，如图所示，由于k_AB=3，k_BC=0，

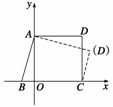∴k_AB·k_BC=0≠-1，

即AB与BC不垂直，故AB、BC都不可作为直角梯形的直角边.

(1)若CD是直角梯形的直角边，则BC⊥CD，AD⊥CD，

∵k_BC=0，∴CD的斜率不存在，从而有x=3.

又k_AD=k_BC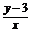，∴=0，即y=3.

此时AB与CD不平行.

故所求点D的坐标为(3，3).

(2)若AD是直角梯形的直角边，

则AD⊥AB，AD⊥CD，

k_A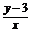D=，k_CD=.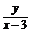

由于AD⊥AB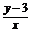，∴·3=-1.

又AB∥CD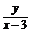，∴=3.

解上述两式可得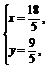

此时AD与BC不平行.

故所求点D的坐标为,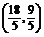

综上可知，使ABCD为直角梯形的点D的坐标可以为(3，3)或.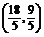

9.已知直线l₁:x+my+6=0,l₂:(m-2)x+3y+2m=0,求m的值，使得：　

(1)l₁与l₂相交；(2)l₁⊥l₂;(3)l₁∥l₂;(4)l₁,l₂重合.　

解(1)由已知1×3≠m(m-2),　

即m²-2m-3≠0,　

解得m≠-1且m≠3.　

故当m≠-1且m≠3时，l₁与l₂相交.　

(2)当1·(m-2)+m·3=0，

即m=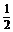时，l₁⊥l₂.　

(3)当=≠,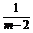

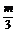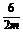即m=-1时，l₁∥l₂.　

(4)当==，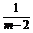　

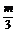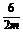即m=3时，l₁与l₂重合.

8.直线2x+3y-6=0关于点M(1，-1)对称的直线方程是　　　 .

答案　 2x+3y+8=0

7.设直线l经过点A(-1，1)，则当点B(2，-1)与直线l的距离最远时，直线l的方程为　　　　 .　

答案　 3x-2y+5=0