
2.(全国2/20)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(I)求从甲、乙两组各抽取的人数; 

(II)求从甲组抽取的工人中恰有1名女工人的概率;
(III)记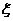 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求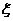 的分布列及数学期望。
的分布列及数学期望。
1.(全国1)甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。
(1)求甲获得这次比赛胜利的概率;
(2)设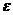 表示从第3局开始到比赛结束所进行的局数,求
表示从第3局开始到比赛结束所进行的局数,求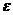 的分布列及数学期望。
的分布列及数学期望。
27.(海南16)等差数列{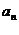 }前n项和为
}前n项和为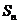 。已知
。已知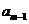 +
+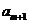 -
-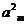 =0,
=0,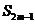 =38,则m=_______
=38,则m=_______
26.(海南7)等比数列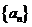 的前n项和为
的前n项和为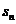 ,且4
,且4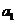 ,2
,2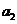 ,
,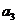 成等差数列。若
成等差数列。若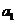 =1,则
=1,则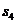 =
=
(A)7 (B)8 (3)15 (4)16
25.(四川22)设数列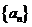 的前
的前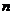 项和为
项和为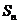 ,对任意的正整数
,对任意的正整数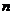 ,都有
,都有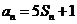 成立,记
成立,记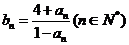 。
。
(I)求数列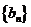 的通项公式;
的通项公式;
(II)记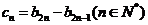 ,设数列
,设数列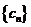 的前
的前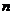 项和为
项和为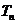 ,求证:对任意正整数
,求证:对任意正整数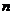 都有
都有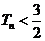 ;
;
(III)设数列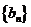 的前
的前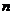 项和为
项和为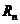 。已知正实数
。已知正实数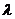 满足:对任意正整数
满足:对任意正整数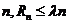 恒成立,求
恒成立,求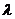 的最小值。
的最小值。
24.(天津22)已知等差数列{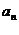 }的公差为d(d
}的公差为d(d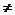 0),等比数列{
0),等比数列{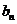 }的公比为q(q>1)。设
}的公比为q(q>1)。设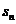 =
=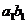 +
+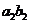 …..+
…..+ 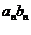 ,
,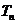 =
=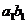 -
-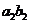 +…..+(-1
+…..+(-1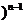
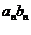 ,n
,n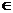
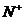

 (1)若
(1)若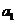 =
=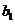 = 1,d=2,q=3,求
= 1,d=2,q=3,求 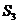 的值;
的值;
(2)若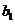 =1,证明(1-q)
=1,证明(1-q)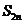 -(1+q)
-(1+q)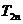 =
=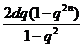 ,n
,n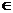
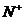 ;
;
(3) 若正数n满足2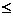 n
n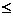 q,设
q,设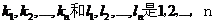 的两个不同的排列,
的两个不同的排列, 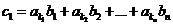 ,
, 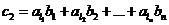 证明
证明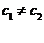 。
。
23.(陕西22)已知数列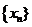 满足,
满足, 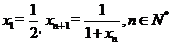 .
.
(1)猜想数列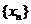 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(2)证明: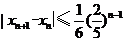 。
。
22.(陕西16)设曲线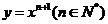 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为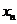 ,令
,令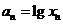 ,则
,则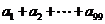 的值为
的值为
21.(辽宁14)等差数列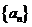 的前
的前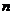 项和为
项和为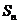 ,且
,且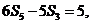 则
则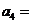
20.(辽宁6)设等比数列{ 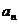 }的前n 项和为
}的前n 项和为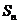 ,若
,若 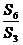 =3 ,则
=3 ,则 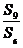 =
= 

(A) 2 (B) 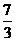 (C)
(C) 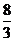 (D)3
(D)3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com