
3.已知数列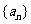 的前
的前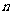 项和为
项和为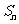 ,且
,且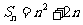 .数列
.数列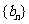 中,
中,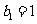 ,
,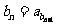
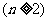 .
.
(1)求数列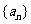 的通项公式;
的通项公式;
(2)若存在常数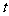 使数列
使数列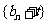 是等比数列,求数列
是等比数列,求数列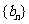 的通项公式;
的通项公式;
(3)求证:①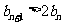 ;②
;②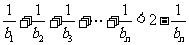 .
.
|
批阅时间 |
等级 |
|
|
|
姓名 作业时间: 2010 年 月 日 星期 作业编号 040
2.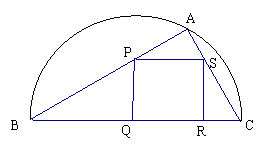 如图,某小区准备绿化一块直径为
如图,某小区准备绿化一块直径为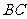 的半圆形空地,
的半圆形空地,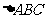 外的地方种草,
外的地方种草,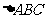 的内接正方形
的内接正方形 为一水池,其余地方种花.若
为一水池,其余地方种花.若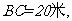
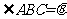 ,设
,设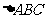 的面积为
的面积为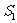 ,正方形
,正方形 的面积为
的面积为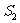 ,将比值
,将比值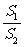 称为“规划合理度”.
称为“规划合理度”.
(1)试用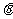 表示
表示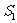 和
和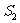 .
.
(2)当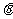 变化时,求“规划合理度”取得最小值时的角
变化时,求“规划合理度”取得最小值时的角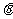 的大小.
的大小.
1. 设椭圆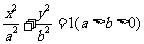 的左焦点为F,上顶点为A,直线AF的倾斜角为
的左焦点为F,上顶点为A,直线AF的倾斜角为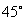 ,
,
(1)求椭圆的离心率;
(2)设过点A且与AF垂直的直线与椭圆右准线的交点为B,过A、B、F三点的圆M恰好与直线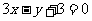 相切,求椭圆的方程及圆M的方程
相切,求椭圆的方程及圆M的方程
7. 已知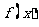 是以2为周期的偶函数,当
是以2为周期的偶函数,当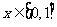 时,
时,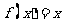 ,且在
,且在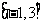 内,关于
内,关于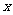 的方程
的方程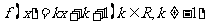 有四个根,则
有四个根,则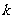 得取值范围是
.
得取值范围是
.
|
批阅时间 |
等级 |
|
|
|
姓名 作业时间: 2010 年 月 日 星期 作业编号 039
6. 数列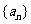 的前
的前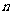 项和是
项和是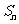 ,若数列
,若数列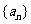 的各项按如下规则排列:
的各项按如下规则排列:
 ,
,
若存在整数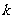 ,使
,使 ,
,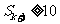 ,则
,则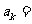 .
.
5.已知函数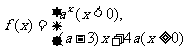 满足对任意
满足对任意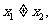 都有
都有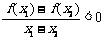 成立,则实数
成立,则实数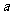 的取值范围是 .
的取值范围是 .
4. 设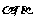 为互不重合的平面,
为互不重合的平面,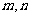 为互不重合的直线,给出下列四个命题:
为互不重合的直线,给出下列四个命题:
①若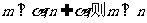 ; ②若
; ②若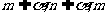 ∥
∥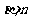 ∥
∥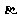 ,则
,则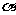 ∥
∥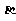 ;
;
③若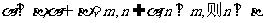 ;④若
;④若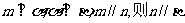 .
.
其中所有正确命题的序号是 .
3. 若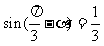 ,则
,则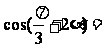 __
____。
__
____。
2. 已知圆的方程为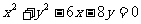 ,设该圆过点
,设该圆过点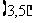 的最长弦和最短弦分别为
的最长弦和最短弦分别为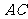 和
和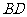 ,则四边形
,则四边形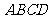 的面积为
。
的面积为
。
1. 已知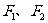 为椭圆
为椭圆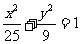 的两个焦点,过
的两个焦点,过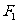 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若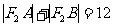 ,则
,则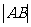 =___________.
=___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com