
1.已知集合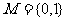 ,则满足
,则满足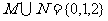 的集合N的个数是( )
的集合N的个数是( )
A.2 B.3 C.4 D.8
3.三个复数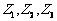 ,其中
,其中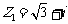 ,
,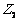 是纯虚数,若这三个复数所对应的向量能构成等边三角形,试确定
是纯虚数,若这三个复数所对应的向量能构成等边三角形,试确定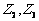 的值。
的值。
作业:课本71页1、2题。
2.若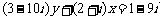 ,求实数
,求实数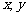 的取值。
的取值。
变式:若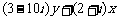 表示的点在复平面的左(右)半平面,试求实数
表示的点在复平面的左(右)半平面,试求实数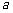 的取值。
的取值。
1.计算
(1)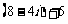 (2)
(2)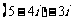 (3)
(3)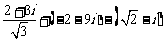
2.小结:两复数相加减,结果是实部、虚部分别相加减,复数的加减运算 都可以按照向量的加减法进行。
都可以按照向量的加减法进行。
2.复数的减法及几何意义:类比实数,规定复数的减法运算是加法运算的逆运 算,即若
算,即若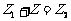 ,则
,则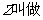
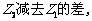
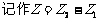 。
。
④讨论:若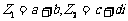 ,试确定
,试确定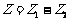 是否是一个确定的值?
是否是一个确定的值?
(引导学生用待定系数法,结合复数的加法运算进行推导,师生一起板演)
 ⑤复数的加
⑤复数的加 法法则及几何意义:
法法则及几何意义: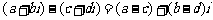 ,复数的减法运算也可以按向量的减法来进行。
,复数的减法运算也可以按向量的减法来进行。
例3.计算(1)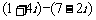 (2)
(2)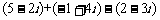 (3)
(3)
练习:已知复数,试画出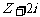 ,
,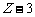 ,
,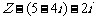
1.复数的加法运算及几何意义
①.复数的加法法则: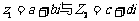 ,则
,则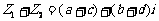 。
。
例 1.计算(1)
1.计算(1)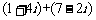 (2)
(2)
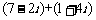 (3)
(3)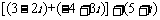
(4)
②.观察上述计算,复数的加法运算是否满足交 换、结合律,试给予验证。
换、结合律,试给予验证。
例2.例1中的(1)、(3)两小题,分别标出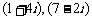 ,
,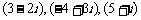 所对应的向量,再画出求和后所对应的向量,看有所发现。
所对应的向量,再画出求和后所对应的向量,看有所发现。
③复数加法的几何意义:复数的加法可以按照向量的加法来进行(满足平行四边形、三角形法则)
3. 同时用坐标和几
同时用坐标和几 何形式表示复数
何形式表示复数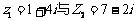 所对应
所对应 的向量,并计算
的向量,并计算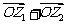
 。向量的加减运算满足何种法则?[来源:学*科*网Z*X*X*K]
。向量的加减运算满足何种法则?[来源:学*科*网Z*X*X*K]
4. 类比向量坐标形式的加减运算,复数的加减运算如何?
2. 试判 断下列复数
断下列复数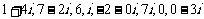 在复平面中落在哪象限?并画出其对应的向量。
在复平面中落在哪象限?并画出其对应的向量。
1. 与复数一一对应的有?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com