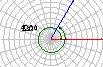
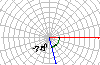
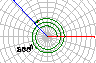
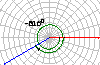
2．已知角的顶点与坐标系原点重合，始边落在x轴的正半轴上，作出下列各角，并指出它们是哪个象限的角？

(1)420°，(2)-75°，(3)855°，(4)-510°．

(答：(1)第一象限角，(2)第四象限角，(3)第二象限角，(4)第三象限角)

1．锐角是第几象限的角？第一象限的角是否都是锐角？小于90°的角是锐角吗？0°-90°的角是锐角吗？

(答：锐角是第一象限角；第一象限角不一定是锐角；小于90°的角可能是零角或负角，故它不一定是锐角；0°-90°的角可能是零角，故它也不一定是锐角．)

总结有关角的集合表示．

锐角：{θ|0°＜θ＜90°}，

0°-90°的角：{θ|0°≤θ≤90°}；

小于90°角：{θ|θ＜90°}．

例1 在0到360度范围内，找出与下列各角终边相同的角，并判断它是哪个象限的角

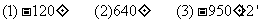
解：⑴∵-120º=-360º+240º，

∴240º的角与-140º的角终边相同，它是第三象限角．

⑵∵640º=360º+280º，

∴280º的角与640º的角终边相同，它是第四象限角．

⑶∵-950º12’=-3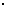360º+129º48’，

∴129º48’的角与-950º12’的角终边相同，它是第三象限角．

例2写出与下列各角终边相同的角的集合S，并把S中在间的角写出来：　 　　　　

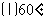
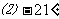
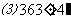
解：(1)

S中在-360°-720间的角是

-1×360°+60°=-280°；

0×360°+60°=60°；

1×360°+60°=420°．

(2)

S中在-360°-720间的角是

0×360°-21°=-21°；

1×360°-21°=339°；

2×360°-21°=699°．

(3)

S中在-360°-720°间的角是

-2×360°+363º14’=-356º46’；

-1×360°+363º14’=3º14’；

0×360°+363º14’=363º14’．

3．终边相同的角　

⑴观察：390°，-330°角，它们的终边都与30°角的终边相同

⑵探究：终边相同的角都可以表示成一个0°到360°的角与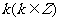个周角的和：

　 390°=30°+360°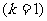　　　　

　 -330°=30°-360°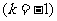　　　 　　　　　　　

　 30°=30°+0×360°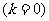　 　　

　1470°=30°+4×360°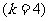　　

　 -1770°=30°-5×360°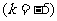　

⑶结论：所有与a终边相同的角连同a在内可以构成一个集合：

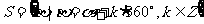
即：任何一个与角a终边相同的角，都可以表示成角a与整数个周角的和

⑷注意以下四点：

(1)

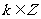
(2) a是任意角；

(3)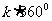与a之间是“+”号，

如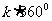-30°，应看成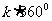+(-30°)；

(4)终边相同的角不一定相等，但相等的角，终边一定相同，终边相同的角有无数多个，它们相差360°的整数倍．

2．“象限角”

为了研究方便，我们往往在平面直角坐标系中来讨论角

角的顶点合于坐标原点，角的始边合于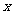轴的正半轴，这样一来，角的终边落在第几象限，我们就说这个角是第几象限的角(角的终边落在坐标轴上，则此角不属于任何一个象限)

例如：30°、390°、-330°是第Ⅰ象限角，300°、-60°是第Ⅳ象限角，585°、1180°是第Ⅲ象限角，-2000°是第Ⅱ象限角等

1．角的概念的推广

⑴“旋转”形成角

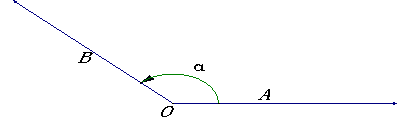
一条射线由原来的位置OA，绕着它的端点O按逆时针方向旋转到另一位置OB，就形成角α．旋转开始时的射线OA叫做角α的始边，旋转终止的射线OB叫做角α的终边，射线的端点O叫做角α的顶点．

突出“旋转”　 注意：“顶点”“始边”“终边”

⑵．“正角”与“负角”“0角”

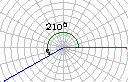
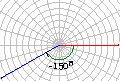
我们把按逆时针方向旋转所形成的角叫做正角，把按顺时针方向旋转所形成的角叫做负角，如图，以OA为始边的角α=210°，β=-150°，γ=660°，

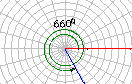
特别地，当一条射线没有作任何旋转时，我们也认为这时形成了一个角，并把这个角叫做零角．记法：角或　 可以简记成

⑶意义

用“旋转”定义角之后，角的范围大大地扩大了

1° 角有正负之分 　　如：a=210°　　 b=-150°　　 g=660°

2° 角可以任意大

　　 实例：体操动作：旋转2周(360°×2=720°) 3周(360°×3=1080°)

3° 还有零角　　 一条射线，没有旋转

角的概念推广以后，它包括任意大小的正角、负角和零角．要注意，正角和负角是表示具有相反意义的旋转量，它的正负规定纯系习惯，就好象与正数、负数的规定一样，零角无正负，就好象数零无正负一样．

2．生活中很多实例会不在改范围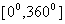

体操运动员转体720º，跳水运动员向内、向外转体1080º

经过1小时时针、分针、秒针转了多少度？

这些例子不仅不在范围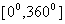，而且方向不同，有必要将角的概念推广到任意角，想想用什么办法才能推广到任意角？(运动)

1．复习：初中是如何定义角的？

从一个点出发引出的两条射线构成的几何图形

这种概念的优点是形象、直观、容易理解，但它是从图形形状来定义角，因此角的范围是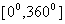，这种定义称为静态定义，其弊端在于“狭隘”

25．(20分)如图所示，在倾角θ=37°的固定斜面上放置一质量M=1kg、长度L=3m的薄平板AB．平板的上表面光滑，其下端B与斜面底端C的距离为7m．在平板的上端A处放一质量m=0.6kg的滑块，开始时使平板和滑块都静止，之后将它们无初速释放．设平板与斜面间、滑块与斜面间的动摩擦因数均为m=0.5，求滑块与平板下端B到达斜面底端C的时间差Δt．(sin37⁰=0.6，cos37⁰=0.8，g=10m/s²)

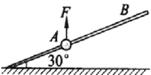
24.(19分)如图所示，一质量为1 kg的小球套在一根固定的直杆上，直杆与水平面夹角θ为30°。现小球在F=20N的竖直向上的拉力作用下，从A点静止出发向上运动，已知杆与球间的动摩擦因数m为。试求：

(1)小球运动的加速度a₁；

(2)若F作用1.2s后撤去，小球上滑过程中距A点最大距离s_m；

(3)若从撤去力F开始计时，小球经多长时间将经过距A点上方为2.25m的B点。