
2.用辗转相除法求52与39的最大公约数的循环次数为( ).
A.1次 B.2次 C.3次 D.5次
1.以下短文摘自古代《孙子算经》一书,其引申出的“大衍求一术”称为“中国剩余原理”:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”答曰( ).
A.二十一 B.二十二 C.二十三 D.二十四
[例1]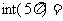 ,
, 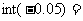 ,
,
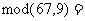 ,
, 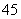
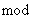 7=
.
7=
.
A.16,-1,4,3 B.15,0,4,3 C.15,-1,3,4 D.15,-1,4,3
错解:根据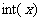 表示不超过
表示不超过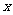 的整数部分,
的整数部分, 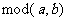 表示
表示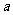 除以
除以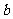 所得的余数,选择B.
所得的余数,选择B.
错因:对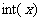 表示的含义理解不透彻,将不超过-0.05的整数错认为是0,将负数的大小比较与正数的大小比较相混淆.
表示的含义理解不透彻,将不超过-0.05的整数错认为是0,将负数的大小比较与正数的大小比较相混淆.
正解:不超过-0.05的整数是-1,所以答案为D.
[例2] 所谓同构数是指此数的平方数的最后几位与该数相等.请设计一算法判断一个大于0且小于1000的整数是否为同构数.
错解: 算法思想:求出输入数的平方,考虑其个位或最后两位或最后三位与输入数是否相等,若相等,则为同构数.
Read x
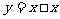
If 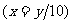 or
or 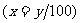 or
or 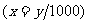 Then
Then
Print x
End if
End
错因:在表示个位或最后两位或最后三位出现错误,“/”仅表示除,y/10,y/100,y/1000都仅仅表示商.
正解:可用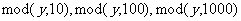 来表示个位,最后两位以及最后三位.
来表示个位,最后两位以及最后三位.
Read x
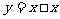
If 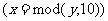 or
or 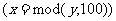 or
or 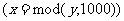 Then
Then
Print x
End if
End
[例3]《孙子算经》中的“物不知数”问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”可以用下面的算法解决:先在纸上写上2,每次加3,加成5除余3的时候停下来,再在这个数上每次加15,到得出7除2的时候,就是答数.
试用流程图和伪代码表示这一算法.
解:流程图为:
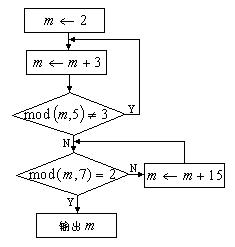
伪代码为:
10 
20 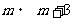
30 If 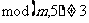 Then Goto 20
Then Goto 20
40 If 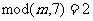 Then
Then
Print 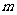
Goto 80
50 End if
60 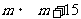
70 Goto 40
80 End
点评:这是孙子思想的体现,主要是依次满足三个整除条件.
[例4]分别用辗转相除法、更相减损法求192与81的最大公约数.
解:辗转相除法:
S1 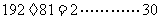
S2
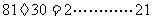
S3
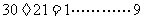
S4
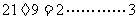
S5 
故3是192 与81 的最大公约数.
更相减损法:
S1
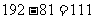
S2 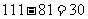
S3 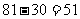
S4 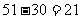
S5 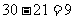
S6 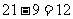
S7 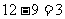
S8 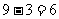
S9
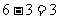
故3 是192与81的最大公约数.
点评:辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少.辗转相除法是当大数被小数整除时停止除法运算,此时的小数就是两者的最大公约数,更相减损术是当大数减去小数的差等于小数时减法停止,较小的数就是最大公约数.
[例5]为了设计用区间二分法求方程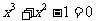 在[0,1]上的一个近似解(误差不超过0.001)的算法,流程图的各个框图如下所示,请重新排列各框图,并用带箭头的流线和判断符号“Y”、“N”组成正确的算法流程图,并写出其伪代码.(其中
在[0,1]上的一个近似解(误差不超过0.001)的算法,流程图的各个框图如下所示,请重新排列各框图,并用带箭头的流线和判断符号“Y”、“N”组成正确的算法流程图,并写出其伪代码.(其中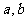 分别表示区间的左右端点)
分别表示区间的左右端点)
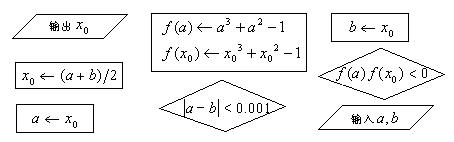
图13-3-2
流程图为
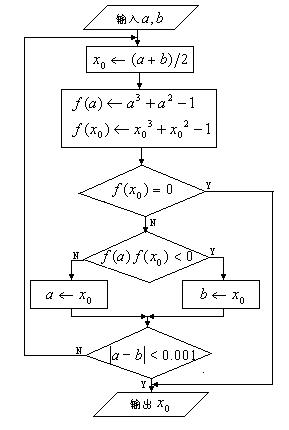
图13-3-3
伪代码为
10 Read 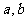
20 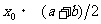
30 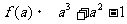
40 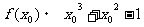
50 If 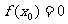 Then Goto 120
Then Goto 120
60 If 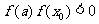 Then
Then
70 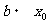
100 End if
80 Else
90 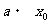
100 End if
110 If 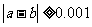 Then Goto 20
Then Goto 20
120 Print 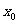
130 End
点评:二分法的基本思想在必修一中已渗透,这里运用算法将二分法求方程近似解的步骤更清晰的表述出来.
[例6] 用秦九韶算法计算多项式 在
在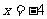 时的值时,
时的值时,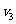 的值为
.
的值为
.
解: 根据秦九韶算法,此多项式可变形为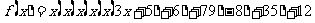
按照从内到外的顺序,依次计算一次多项式当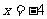 时的值:
时的值:
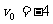
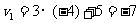
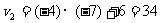
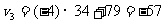
故当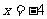 时多项式的值为
时多项式的值为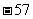 .
.
点评:秦九韶算法的关键是n次多项式的变形.
把一个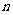 次多项式
次多项式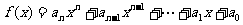 改写成
改写成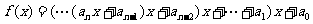 ,求多项式的值,首先计算最内层括号内一次多项式的值,然后由内向外逐层计算一次多项式的值,这样把求
,求多项式的值,首先计算最内层括号内一次多项式的值,然后由内向外逐层计算一次多项式的值,这样把求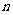 次多项式的值问题转化为求
次多项式的值问题转化为求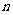 个一次多项式的值的问题,这种方法成为秦九韶算法.这种算法中有反复执行的步骤,因此,可考虑用循环结构实现.
个一次多项式的值的问题,这种方法成为秦九韶算法.这种算法中有反复执行的步骤,因此,可考虑用循环结构实现.
4.用二分法求方程近似解,必须先判断方程在给定区间[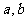 ]上是否有解,即
]上是否有解,即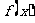 连续且满足
连续且满足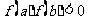 .并在二分搜索过程中需对中点处函数值的符号进行多次循环判定,故需要选择结构、循环结构,即可用Goto 语句和条件语句实现算法.
.并在二分搜索过程中需对中点处函数值的符号进行多次循环判定,故需要选择结构、循环结构,即可用Goto 语句和条件语句实现算法.
3.辗转相除法与更相减损术求最大公约数的联系与区别:
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显.
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.
2.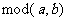 表示
表示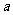 除以
除以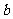 所得的余数,也可用
所得的余数,也可用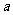
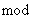
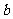 表示.
表示.
1.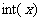 表示不超过
表示不超过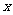 的整数部分,如
的整数部分,如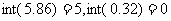 ,但当
,但当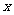 是负数时极易出错,如
是负数时极易出错,如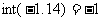 就是错误的,应为-2.
就是错误的,应为-2.
2.更相减损术的步骤:(1)任意给出两个正数,判断它们是否都是偶数.若是,用2约简;若不是,执行第二步.(2)以较大的数减去较小的数,接着把较小的数与所得的差比较,并以大数减小数.继续这个操作,直到所得的数相等为止,则这个数(等数)就是所求的最大公约数.
(3)二分法求方程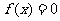 在区间
在区间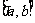 内的一个近似解
内的一个近似解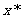 的解题步骤可表示为
的解题步骤可表示为
S1 取[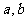 ]的中点
]的中点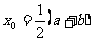 ,将区间
一分为二;
,将区间
一分为二;
S2 若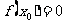 ,则
,则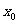 就是方程的根;否则判别根
就是方程的根;否则判别根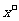 在
在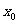 的左侧还是右侧:
的左侧还是右侧:
若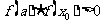 ,
,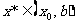 ,以
,以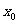 代替
代替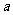 ;
;
若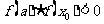 ,则
,则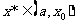 ,以
,以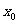 代替
代替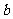 ;
;
S3 若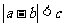 ,计算终止,此时
,计算终止,此时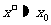 ,否则转S1.
,否则转S1.
1.算法设计思想:
(1)“韩信点兵-孙子问题”对正整数m从2开始逐一检验条件,若三个条件中有任何一个不满足,则m递增1,一直到m同时满足三个条件为止(循环过程用Goto语句实现)
(2)用辗转相除法找出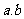 的最大公约数的步骤是:计算出
的最大公约数的步骤是:计算出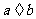 的余数
的余数 ,若
,若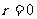 ,则
,则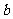 为
为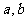 的最大公约数;若
的最大公约数;若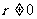 ,则把前面的除数
,则把前面的除数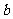 作为新的被除数,继续运算,直到余数为0,此时的除数即为正整数
作为新的被除数,继续运算,直到余数为0,此时的除数即为正整数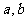 的最大公约数.
的最大公约数.
5. 将100名学生的一门功课的成绩依次输入并计算输出平均成绩.
§ 13.3 算法案例
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com