
4.分式不等式
分式不等式的等价变形: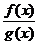 >0
>0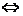 f(x)·g(x)>0,
f(x)·g(x)>0,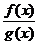 ≥0
≥0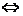
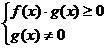 。
。
3.一元二次不等式
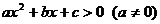 或
或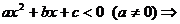 分
分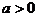 及
及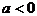 情况分别解之,还要注意
情况分别解之,还要注意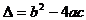 的三种情况,即
的三种情况,即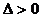 或
或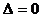 或
或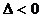 ,最好联系二次函数的图象.
,最好联系二次函数的图象.
2.一元一次不等式
解一元一次不等式(组)及一元二次不等式(组)是解其他各类不等式的基础,必须熟练掌握,灵活应用。
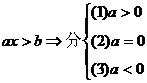 情况分别解之。
情况分别解之。
1.不等式的解法
解不等式是求定义域、值域、参数的取值范围时的重要手段,与“等式变形”并列的“不等式的变形”,是研究数学的基本手段之一。
高考试题中,对解不等式有较高的要求,近两年不等式知识占相当大的比例。
(1)同解不等式((1)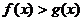 与
与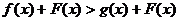 同解;
同解;
(2)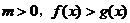 与
与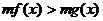 同解,
同解,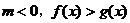 与
与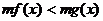 同解;
同解;
(3)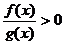 与
与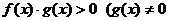 同解);
同解);
4.对含参数的不等式,要加强分类讨论思想的复习,学会分析引起分类讨论的原因,合理分类,不重不漏.
3.在函数、不等式、数列、解析几何、导数等知识网络的交汇点命题,特别注意与函数、导数综合命题这一变化趋势;
分析近几年的高考试题,本将主要考察不等式的解法,综合题多以与其他章节(如函数、数列等)交汇。从题型上来看,多以比较大小,解简单不等式以及线性规划等,解答题主要考察含参数的不等式的求解以及它在函数、导数、数列中的应用.
预测2010年高考的命题趋势:
1.结合指数、对数、三角函数的考察函数的性质,解不等式的试题常以填空题、解答题形式出现;
2.一元二次不等式
①.经历从实际情境中抽象出一元二次不等式模型的过程;
②通过函数图像了解一元二次不等式与相应函数、方程的联系;
③会解一元二次不等式,对给定的一元二次不等式,尝试设计求解的程序框图
3二元一次不等式组与简单线性规划问题
①从实际情境中抽象出二元一次不等式组;
②了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组;
③从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.
1.不等关系
通过具体情境,感受在现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com