
(Ⅱ)当 时,若圆心为
时,若圆心为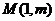 的圆和圆
的圆和圆 外切且与直线
外切且与直线 、
、 都相切,求圆
都相切,求圆 的方程;
的方程;
(Ⅰ)若 、
、 都和圆
都和圆 相切,求直线
相切,求直线 、
、 的方程;
的方程;
已知圆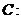
 ,相互垂直的两条直线
,相互垂直的两条直线 、
、 都过点
都过点 .
.
18.(本小题满分16分)
再分别取 、
、 的中点
的中点 、
、 ,连结
,连结 、
、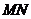 ,易知
,易知 是
是 的中点,
的中点, 是
是 的中点,从而当点
的中点,从而当点 满足
满足 时,有
时,有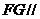 平面
平面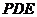 。………………………………………14分
。………………………………………14分
又 ,所以平面
,所以平面 ∥平面
∥平面 ……………………………………………12分
……………………………………………12分
由 ∥
∥ ,
,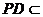 平面
平面 ,得
,得 ∥平面
∥平面 ,
,
由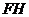 ∥
∥ ,
,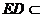 平面
平面 ,得
,得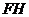 ∥平面
∥平面 ;
;
(Ⅲ)过点 作
作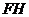 ∥
∥ 交
交 于
于 ,再过
,再过 作
作 ∥
∥ 交
交 于
于 ,连结
,连结 。
。
(Ⅱ)证:因为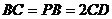 ,A是PB的中点,所以ABCD是矩形,又E为BC边的中点,所以AE⊥ED。又由
,A是PB的中点,所以ABCD是矩形,又E为BC边的中点,所以AE⊥ED。又由 平面
平面 ,得
,得
 ,且
,且 ,所以
,所以 平面
平面 ,而
,而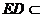 平面
平面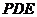 ,故平面
,故平面 平面
平面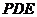 …………………………………………………………9分
…………………………………………………………9分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com